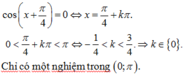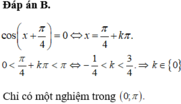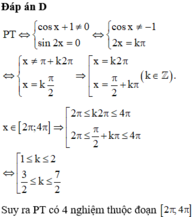Tìm nghiệm x thuộc [0 ; 2 pi ] của pt sin 2x = căn 2/ 2
DN
Những câu hỏi liên quan
Tìm số nghiệm thuộc khoảng ( 0 ; π ) của phương trình cos ( x + π 4 ) = 0.
A. 0
B. 1
C. 2
D. 3
Tìm số nghiệm thuộc khoảng
0
,
π
của phương trình
cos
x
+
π
4
0
A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Tìm số nghiệm thuộc khoảng 0 , π của phương trình cos x + π 4 = 0
A. 0
B. 1
C. 2
D. 3
Tìm tất cả các nghiệm của phương trình sin x + sin 2x + sin3x = 0 thuộc ( 0 ; π )
A. 3
B. 4
C. 5
D. 6
tìm m để phương trình :
\(\left(m+1\right)x^2-\left(8m+1\right)x+6m=0\)
a,có nghiệm thuộc khoảng (1;dương vô cùng)
b, có đúng 1 nghiệm thuộc (0;1)
a.
- Với \(m=-1\Rightarrow x=\dfrac{6}{7}\) (ktm)
- Với \(m\ne-1\)
\(\Delta=\left(8m+1\right)^2-24m\left(m+1\right)=40m^2-8m+1>0;\forall m\) \(\Rightarrow\) pt luôn có 2 nghiệm pb
Để pt có 2 nghiệm thỏa mãn: \(x_1< x_2\le1\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)\ge0\\\dfrac{x_1+x_2}{2}< 1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_1\right)+1\ge0\\x_1+x_2< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6m}{m+1}-\dfrac{8m+1}{m+1}+1\ge0\\\dfrac{8m+1}{m+1}< 2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-m}{m+1}\ge0\\\dfrac{6m-1}{m+1}< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-1< m\le0\\-1< m< \dfrac{1}{6}\end{matrix}\right.\) \(\Rightarrow-1< m\le0\)
\(\Rightarrow\) Pt có nghiệm thuộc khoảng đã cho khi: \(\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
b.
Đặt \(f\left(x\right)=\left(m+1\right)x^2-\left(8m+1\right)x+6m\)
Pt đã cho có đúng 1 nghiệm thuộc (0;1) khi:
\(f\left(0\right).f\left(1\right)< 0\)
\(\Leftrightarrow6m\left(m+1-8m-1+6m\right)< 0\)
\(\Leftrightarrow-6m^2< 0\)
\(\Leftrightarrow m\ne0\)
Đúng 2
Bình luận (0)
cho pt x2-2(m-1)x+m2-3m0(*) a) tìm m để 2 nghiệm trái dấu b) tìm m để pt có đùng 1 nghiệm âmc)tìm m để pt có 1 nghiệm 0 tìm nghiệm còn lạid) tìm ht liên hệ giữa 2 nghiệm k phụ thuộc vào m e) tìm m để pt có 2 nghiệm tm c12+x228
Đọc tiếp
cho pt x2-2(m-1)x+m2-3m=0(*)
a) tìm m để 2 nghiệm trái dấu
b) tìm m để pt có đùng 1 nghiệm âm
c)tìm m để pt có 1 nghiệm =0 tìm nghiệm còn lại
d) tìm ht liên hệ giữa 2 nghiệm k phụ thuộc vào m
e) tìm m để pt có 2 nghiệm tm c12+x22=8
Cho f(x)=\(-x^2+\left(2\sqrt{m}-1\right)x-m+\sqrt{m}\)
a)tìm m để f(x) >=0 vô nghiệm(lớn hơn = 0)
b)tìm m để f(x) >=0 với mọi x thuộc [1;2]
\(a=-1< 0;\Delta=\left(2\sqrt{m}-1\right)^2+4\left(\sqrt{m}-m\right)=4m-4\sqrt{m}+1+4\sqrt{m}-4m=1>0\)
a/ \(f\left(x\right)\ge0\) vô nghiệm \(\Leftrightarrow f\left(x\right)< 0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(tm\right)\\\Delta< 0\left(voly\right)\end{matrix}\right.\)
Vậy ko tồn tại m để ....
b/ \(f\left(x\right)\ge0,\forall x\in\left[1;2\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left[{}\begin{matrix}1< x_1< x_2\\x_1< x_2< 2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1.f\left(1\right)>0\\\dfrac{x_1+x_2}{2}-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}-1.f\left(2\right)>0\\\dfrac{x_1+x_2}{2}-2< 0\end{matrix}\right.\end{matrix}\right.\)
\(\left(1\right)\left\{{}\begin{matrix}-1+2\sqrt{m}-1-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-3\sqrt{m}+2>0\\\sqrt{m}>\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 1\\m>2\end{matrix}\right.\\m>\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow m>\dfrac{9}{4}\)
\(\left(2\right)\left\{{}\begin{matrix}-4+4\sqrt{m}-2-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-5\sqrt{m}+6>0\\\sqrt{m}< \dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 2\\m>3\end{matrix}\right.\\0\le m< \dfrac{25}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{9}{4}\\0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm số nghiệm thuộc đoạn
2
π
,
4
π
của phương trình
sin
2
x
cos
x
+
1
...
Đọc tiếp
Tìm số nghiệm thuộc đoạn 2 π , 4 π của phương trình sin 2 x cos x + 1 = 0
A. 5
B. 6
C. 3
D. 4
tìm m để phương trình x^2-(m+3)x+2m+2=0 có đúng 1 nghiệm thuộc (-∞;3]
\(x^2-\left(m+3\right)x+2m+2=0\Leftrightarrow\left(x-2\right)\left(x-m-1\right)=0\left(1\right)\)
\(\Delta=\left(m+3\right)^2-4\left(2m+2\right)=m^2+6m+9-8m-8=m^2-2m+1=\left(m-1\right)^2\ge0\left(\forall m\right)\)
\(\Rightarrow\left(1\right)\) \(luôn\) \(có\) \(nghiệm\) \(\forall m\)
\(\left(1\right)\Rightarrow\left[{}\begin{matrix}x=2\in(-\text{∞};3]\\x=m+1\end{matrix}\right.\)
\(\left(1\right)\) \(có\) \(đúng\) \(1\) \(nghiệm\) \(\in(-\text{∞};3]\) \(\Leftrightarrow\left[{}\begin{matrix}x=m+1=2\\x=m+1>3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m>2\end{matrix}\right.\)
\(\Rightarrow\left\{1\right\}\cup\left(2;+\text{∞}\right)\)
\(\)
Đúng 1
Bình luận (0)
Cho PT : \(x^2-2\left(m+1\right)x+m^2=0\)
a) Tìm m để PT có 2 nghiệm phân biệt
b) Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào m
Phương trình có 2 nghiệm pb khi:
\(\Delta'=\left(m+1\right)^2-m^2>0\Leftrightarrow2m+1>0\)
\(\Rightarrow m>-\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x_1+x_2-2}{2}=m\\x_1x_2=m^2\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\left(\dfrac{x_1+x_2-2}{2}\right)^2\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
Đúng 1
Bình luận (0)
a,Phương trình có 2 nghiệm pb khi: \(\Delta'>0\Rightarrow\left(m+1\right)^2-m^2>0\Leftrightarrow2m+1>0\Leftrightarrow m>\dfrac{-1}{2}\)
Đúng 0
Bình luận (0)
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4