Bài 14:
a) Viết phương trình đường thẳng đi qua điểm A ( 4 ; -5 ) và có hệ số góc a = -2
b) Viết phương trình đường thẳng qua hai điểm B ( 0 ;1 ) và C ( 8 : -1)
c) Ba điểm sau đây có thẳng hàng hay không : M ( -2 ; -3 ) , N ( -6 ; -5 ) , P ( 1 ; 1)
TK
Những câu hỏi liên quan
Bài 5. Trong mặt phẳng Oxy, cho điểm A(2;-1) và đường thẳng d : 3x-4y+5=0
a) Viết phương trình đường thẳng đi qua A và vuông góc với d
b) Viết phương trình đường thẳng đi qua A và song song với d.
c) Viết phương trình đường thẳng song song với d và cách A một khoảng bằng 3
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
Đúng 0
Bình luận (0)
Câu 3: Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A(1;2), B(-3;0).Câu 4: Viết phương trình tổng quát đường cao AH của tam giác ABC biết A(1;-3), B(2;0), C(3;-1).Câu 5: Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A(3;-1), B(2;3)Câu 9: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc bút. Tính xác suất để hai chiếc bút lấy được cùng màu?Câu 10: Xếp 5 quyển sách Toán và 5 quyển sách Văn khác nhau lên một kệ dài. Tính...
Đọc tiếp
Câu 3: Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A(1;2), B(-3;0).
Câu 4: Viết phương trình tổng quát đường cao AH của tam giác ABC biết A(1;-3), B(2;0), C(3;-1).
Câu 5: Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A(3;-1), B(2;3)
Câu 9: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc bút. Tính xác suất để hai chiếc bút lấy được cùng màu?
Câu 10: Xếp 5 quyển sách Toán và 5 quyển sách Văn khác nhau lên một kệ dài. Tính xác suất để 2 quyển sách cùng một môn nằm cạnh nhau.
5:
Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3
=>a=-4 và b=11
=>y=-4x+11
4:
vecto BC=(1;-1)
=>AH có VTPT là (1;-1)
Phương trình AH là:
1(x-1)+(-1)(y+3)=0
=>x-1-y-3=0
=>x-y-4=0
Đúng 1
Bình luận (0)
Bài 2: Cho (d): y = 2x + 3; (d’): y = - 3x - 2
a/ Xác định tọa độ giao điểm A của (d) và (d’)
b/ Viết phương trình đường thẳng đi qua A và có hoành độ luôn bằng tung độ
c/ Viết phương trình đường thẳng đi qua A và vuông với trục hoành
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài tập 1: Cho đường thẳng đi qua điểm và có vectơ pháp tuyến . Viết phương trình tham số và phương trình tổng quát của đường thẳng .Bài tập 2: Cho tam giác ABC có . a) Viết phương trình tổng quát của cạnh BC. b) Viết phương trình tham số của đường t...
Xem chi tiết
Cho 2 điểm A(1;-2) ; B(0;4) a. Viết phương trình tham số của đường thẳng đi qua hai điểm A và B B. Viết phương trình tổng quát của đường thẳng đi qua hai điểm A và B
a: vecto AB=(-1;6)
=>VTPT là (6;1)
Phương trình tham số là;
x=1-t và y=-2+6t
b: PTTQ là:
6(x-1)+1(y+2)=0
=>6x-6+y+2=0
=>6x+y-4=0
Đúng 0
Bình luận (0)
Bài 4.
a) Lập phương trình đường thẳng (d) đi qua điểm M (-1; 3) và có hệ số góc bằng 2.
b) Lập phương trình đường thẳng (d) đi qua M(3; 5) và song song với đường thẳng (d’) có phương trình y = 2x
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
Đúng 1
Bình luận (2)
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)
1. Cách viết phương trình đường thẳng đi qua 2 điểm1.1. Cách 1: Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)Gọi phương trình đường thẳng có dạng d: yax+bVì A và B thuộc phương trình đường thẳng d nên ta có hệThay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.1.2. Cách 2 giải nhanhTổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).Cách giải:Giả sử đường thẳng đ...
Đọc tiếp
1. Cách viết phương trình đường thẳng đi qua 2 điểm
1.1. Cách 1:
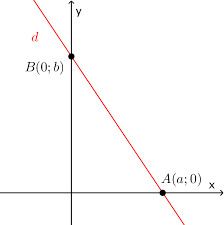
Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)
Gọi phương trình đường thẳng có dạng d: y=ax+bVì A và B thuộc phương trình đường thẳng d nên ta có hệ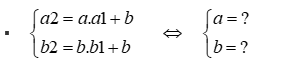
Thay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.1.2. Cách 2 giải nhanh
Tổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).
Cách giải:
Giả sử đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2) có dạng: y = ax + b (y*)
Vì (y*) đi qua điểm A(x1;y1) nên ta có: y1=ax1 + b (1)
Vì (y*) đi qua điểm B(x2;y2) nên ta có: y2=ax2 + b (2)
Từ (1) và (2) giải hệ ta tìm được a và b. Thay vào sẽ tìm được phương trình đường thẳng cần tìm.
Bài tập ví dụ viết phương trình đường thẳng đi qua 2 điểm
Bài tập 1: Viết phương trình đường thẳng đi qua hai điểm A (1;2) và B(0;1).
Bài giải:
Gọi phương trình đường thẳng là d: y=ax+by=ax+b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có:
⇔ 
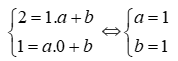
Thay a=1 và b=1 vào phương trình đường thẳng d thì d là: y=x+1
Vậy phương trình đường thẳng đi qua 2 điểm A và B là : y=x+1
Bài tập 2: Cho Parabol (P):y=–ײ . Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc (P) và có hoành độ lần lượt là 1 và 2.
Bài giải
Với bài toán này chúng ta chưa biết được tọa độ của A và B là như nào. Tuy nhiên bài toán lại cho A và B thuộc (P) và có hoành độ rồi. Chúng ta cần đi tìm tung độ của điểm A và B là xong.
Tìm tọa độ của A và B:
Vì A có hoành độ bằng -1 và thuộc (P) nên ta có tung độ y =−(1)²=–1 => A(1;−1)
Vì B có hoành độ bằng 2 và thuộc (P) nên ta có tung độ y =–(2)²=−4 ⇒ B(2;−4) còn cách khác k ?
a) Viết phương trình đường thẳng đi qua gốc tọa độ O và điểm A(-1;3)
b) Viết phương trình đường thẳng thứ 2 đi qua điểm B(-3;2) và vuông góc đường thẳng OA
c) Viết phương trình đường thẳng thứ 3 đi qua điểm C(1;-2) và ssong song đường thẳng OA
Giúp mình nha, cảm ơn