tìm GTNN ( tìm giá trị nhỏ nhất )
a; A= / x- 1/ + / y+2 / + 3
b; B= / 3- y /+ ( x+1)2 -5 cảm ơn nha tuy mình chọn Hân nhưng bài của 66 44... hay hơn nhưng cậu ấy có 1 tick rồi nên hihi
a)Cho biểu thức A=|x-3|+5 có giá trị nhỏ nhất (GTNN). Tìm GTNN đó
b)Cho biểu thức B=20-|x+2| có giá trị lớn nhất (GTLN) . Tìm GTLN đó
a)\(\sqrt{x-4}-2\) tìm x để đạt giá trị nhỏ nhất , tìm GTNN đó
ĐK: `x-4>=0 <=>x>=4`
`\sqrt(x-4)>=0 forall x`
`<=>\sqrt(x-4)-2>=-2`
`=> (\sqrt(x-4)-2)_(min) =-2<=> x=4`
bài 1: tìm x biết |x+2| + |2x-3| = 5
bài 2: tìm GTNN của biểu thức A = |x-102| + |2-x|
bài 3: cho biểu thức A = 3/(x-1)
a/ Tìm số nguyên x để A đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó
b/ tìm số nguyên x để A đạt giá trị lớn nhất và tìm giá trị lớn nhất đó
bài 2
Ta có:
\(A=\left|x-102\right|+\left|2-x\right|\Rightarrow A\ge\left|x-102+2-x\right|=-100\Rightarrow GTNNcủaAlà-100\)đạt được khi \(\left|x-102\right|.\left|2-x\right|=0\)
Trường hợp 1: \(x-102>0\Rightarrow x>102\)
\(2-x>0\Rightarrow x< 2\)
\(\Rightarrow102< x< 2\left(loại\right)\)
Trường hợp 2:\(x-102< 0\Rightarrow x< 102\)
\(2-x< 0\Rightarrow x>2\)
\(\Rightarrow2< x< 102\left(nhận\right)\)
Vậy GTNN của A là -100 đạt được khi 2<x<102.
Gấp ạ mọi người giúp em với:<
1. Q = |-2x+3| + \(\dfrac{3}{4}\)
- Tìm GTNN (Giá trị nhỏ nhất) của Q
2. H = (2x+1)\(^2\) - 1\(\dfrac{1}{2}\)
- Tìm GTNN của H
3. M = =(2x+1)\(^2\) + 2021
- Tìm GTLN (Giá trị lớn nhất) của M
3:
Ta có: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Leftrightarrow\left(2x+1\right)^2+2021\ge2021\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất
\(A=|x+3|+1\)
\(B=-|2x-1|+3\)
Cho mị hỏi cái này nx đc hôg: Khi nào sử dụng GTLN; GTNN
\(A=\left|x+3\right|+1\ge1\forall x\)
Dấu '=' xảy ra khi x=-3
\(B=-\left|2x-1\right|+3\ge3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(A=\left|x+3\right|+1\) (GTNN)
Vì \(\left|x+3\right|\ge0\) nên \(\left|x+3\right|+1\ge1\) hay \(A\ge1\)
Dấu ''='' xảy ra khi x=-3
\(B=-\left|2x+1\right|+3\) (GTLN)
Vì \(\left|2x+1\right|\ge0\) nên \(-\left|2x+1\right|+3\le3\) hay \(B\le3\)
Dấu ''='' xảy ra khi x=\(\dfrac{-1}{2}\)
Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của z , biết z là số phức thỏa mãn z − i = 2 .
A. z min = 1 ; z max = 3 .
B. z min = 3 ; z max = 9 .
C. z min = 1 ; z max = 9 .
D. z min = 0 ; z max = 3 .
Đáp án A
Gọi z = x + i y ; x , y ∈ ℝ .
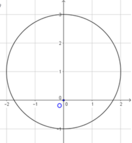
z − i = 2 ⇔ x + i y − i = 2 ⇔ x 2 + y − 1 2 = 4 ⇒ x 2 + y 2 = 2 y + 3
Do đó tập hợp các số phức z là đường tròn tâm I(0;1), bán kính R=2 (như hình vẽ).
z = x 2 + y 2 = 2 y + 3 , − 1 ≤ y ≤ 3 − 2 ≤ x ≤ 2 .
Dễ thấy,
z min = 2 − 1 + 3 = 1 ; z max = 2.3 + 3 = 3.
1/ Tìm giá trị nhỏ nhất của biểu thức B= 2I3x-6I - 4
2/ Tìm x thuộc Z để biểu thức D= I x-2 I + I x-8 I đạt Gía trị nhỏ nhất
3/ Tìm GTNN của biểu thức B = I x-2017 I + I x-1 I
A= I x-2017 I + I x-2 I
4/ với giá trị nào của x,y thì biểu thức C = I x-100 I + I y+20 I - 1 có giá trị nhỏ nhất . Tìm GTNN
5/ Với giá trị nào của x thì biểu thức A= 100 - I x+5 I có giá trị lớn nhất. Tìm GTLN đó
Cho biểu thức 4x+9/x-1
a, B có giá trị nhỏ nhất. Tìm GTNN
b, B có GTLN. Tìm GTLN
Tìm giá trị( LN ) giá trị nhỏ nhất ( gtnn) của các biểu thức sau:
A) A= x^2+3x+1
B) B= 2x^2+6x+y^2+2xy+12
C) C= 2x-x^2
\(A=\left(x^2+2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{5}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{5}{4}\ge-\dfrac{5}{4}\\ A_{min}=-\dfrac{5}{4}\Leftrightarrow x=-\dfrac{3}{2}\\ B=\left(x^2+2xy+y^2\right)+\left(x^2+6x+9\right)+3\\ B=\left(x+y\right)^2+\left(x+3\right)^2+3\ge3\\ B_{min}=3\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\\ C=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1\le1\\ C_{max}=1\Leftrightarrow x=1\)
Tìm GTNN(giá trị nhỏ nhất)
B=2|3x-1|-4
Vì | 3x - 1 |\(\ge\)0\(\forall\)x
=> B = 2 | 3x - 1 | - 4 \(\ge\)- 4
Dấu "=" xảy ra <=> 2 | 3x - 1 | = 0 <=> 3x - 1 = 0 <=> x = 1/3
Vậy minB = - 4 <=> x = 1/3
B = 2| 3x - 1 | - 4
Ta có 2| 3x - 1 | ≥ 0 ∀ x => 2| 3x - 1 | - 4 ≥ -4
Đẳng thức xảy ra <=> 3x - 1 = 0 => x = 1/3
=> MinB = -4 <=> x = 1/3
Ta có : |3x-1|\(\ge\)0
=> 2|3x-1|\(\ge\)0
Theo bài ra ta có : B đạt GTNN nên 2|3x-1| phải có giá trị nhỏ nhất
Mà 2|3x-1|\(\ge\)0
Dấu ''='' xảy ra khi : 2|3x-1|=0
<=> |3x-1|=0
=> 3x-1=0
3x=1
=> x=1/3
Vậy GTNN của B = -4 khi và chỉ khi x=1/3