Cho: a,b∈ Z; (a,b)=1. CMR: \(\frac{8a+3b}{5a+2b}\) Tối giản
DM
Những câu hỏi liên quan
Cho 3 số a, b, c khác 0 và : a(y + z) = b(x + z) =c(z + y) Chứng minh rằng : y - z /a(b - c) = z - x / b(c - a) = x - y / c(a - b)
a,Tìm x,y,z biết: dfrac{y+z+1}{x}dfrac{x+z+2}{y}dfrac{x+y-3}{z}dfrac{1}{x+y+z}b,Cho dfrac{a}{b}dfrac{b}{c}dfrac{c}{d}. Chứng minh rằng: (dfrac{a+b+c}{b+c+d})3dfrac{a}{d}c,Cho dfrac{a}{b}dfrac{c}{d}. Chứng minh rằng: dfrac{5a+3b}{5c+3d}dfrac{5a-3b}{5c-3d}d,Cho dfrac{3x-2y}{4}dfrac{2z-4x}{3}dfrac{4y-3z}{2}.Chứng minh rằng: dfrac{x}{2}dfrac{y}{3}dfrac{z}{4}
Đọc tiếp
a,Tìm x,y,z biết: \(\dfrac{y+z+1}{x}\)=\(\dfrac{x+z+2}{y}\)=\(\dfrac{x+y-3}{z}\)=\(\dfrac{1}{x+y+z}\)
b,Cho \(\dfrac{a}{b}\)=\(\dfrac{b}{c}\)=\(\dfrac{c}{d}\). Chứng minh rằng: (\(\dfrac{a+b+c}{b+c+d}\))3=\(\dfrac{a}{d}\)
c,Cho \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). Chứng minh rằng: \(\dfrac{5a+3b}{5c+3d}\)=\(\dfrac{5a-3b}{5c-3d}\)
d,Cho \(\dfrac{3x-2y}{4}\)=\(\dfrac{2z-4x}{3}\)=\(\dfrac{4y-3z}{2}\).Chứng minh rằng: \(\dfrac{x}{2}\)=\(\dfrac{y}{3}\)=\(\dfrac{z}{4}\)
b/ \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
\(\Rightarrow\left(\dfrac{a}{b}\right)^3=\dfrac{a}{d}\left(1\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\)
=> \(\left(\dfrac{a}{b}\right)^3=\left(\dfrac{a+b+c}{c+d+b}\right)^3\) (2)Từ (1) và (2)=>đpcm
Đúng 1
Bình luận (1)
Bài 1: Cho (a+b-c)/c = (b+c-a)/a = (c+a-b)/b. Tính
P= (1+b/a) . (1+c/b) . (1+a/c)
Bài 2: Cho x/(y+z+t) = y/(z+t+x) = z/(t+x+y) = t/(x+t+z). Tính
(x+y)/(z+t) + (y+z)/(t+x) + (z+t)/(x+y) + (t+x)/(y+z)
Bài 1: áp dụng tính chất dãy tỉ số bằng nhau ta được:
(a+b-c)/c=(b+c-a)/a=(c+a-b)/b=(a+b-c+b+c-a+c+a-b)/(a+b+c)=(a+b+c)/(a+b+c0=1
Do đó: (a+b+c)/c=1 suy ra a+b+c=c suy ra a+b=c-c=0 nên a=b (1)
(b+c-a)/a=1 suy ra b+c-a=a suy ra a+c-a=a (b=a) suy ra c=a (2) Từ (1) và(2) ta có: a=b=c
Suy ra:P= (1+b/a).(1+c/b).(1+a/c)=(1+a/a).(1+a/a).(1+a/a)=(1+1).(1+1).(1+1)=2.2.2=8
Bài 2: bạn cũng áp dụng tính chất dãy tỉ bằng nhau rồi xét giống bài 1 là ra
Đúng 0
Bình luận (0)
a)cho a,b,c >0
CMR (a+1)(b+1)(a+c)(b+c)>=16abc
b)cho x,y,z>0 CMR x+y/z+y+z/x+z+x/y>= 6
c)cho a>=1, b>=1 CMR a căn b-1+b căn a-1 <=ab
Cho a; b thuộc Z ; a>Z ; b>Z
Chứng minh: a+b < a.b
Cho a thuộc Z+,b thuộc Z-;hãy so sánh IaI và IbI trong các trường hợp
a)a+b thuộc Z+
b)a+b thuộc Z-
Cho a(y+z)=b(z+x)=c(x+y).Chứng minh y-z/a(b-c)= z-x/b(c-a) = x-y/ c(a-b)
Cho a thuoc Z+ b thuoc Z- .Hay so sanh IaI va IbI trong cac truong hop
A)a+b thuoc Z+
B)a+b thuoc Z-
Cho a thuộc Z+,b thuộc Z- .Hãy so sánh IaI,IbI trong các trường hợp sau:
a)a+b thuộc Z+
b)a+b thuộc Z-
Cho số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa
z
+
4
+
z
−
4
10
và
z
-
6
lớn nhất. T...
Đọc tiếp
Cho số phức z = a + b i a , b ∈ ℝ thỏa z + 4 + z − 4 = 10 và z - 6 lớn nhất. Tính S = a + b .
A. S = 5
B. S = -5
C. S = 11
D. S = -3
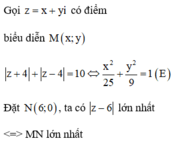
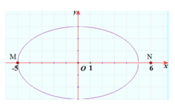
Vẽ trên hệ trục Oxy, nhận thấy MN lớn nhất khi M. Khi đó ![]()
Chọn B
Đúng 0
Bình luận (0)


