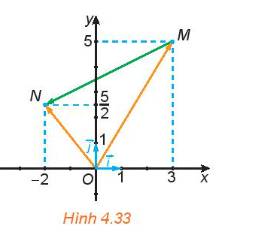
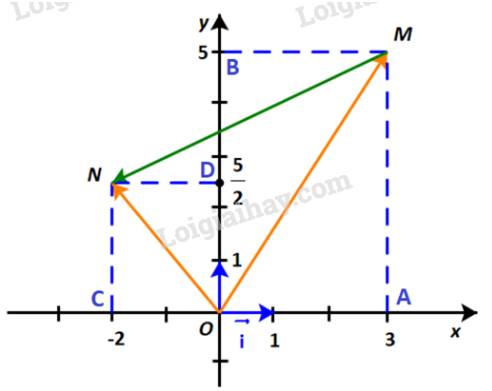
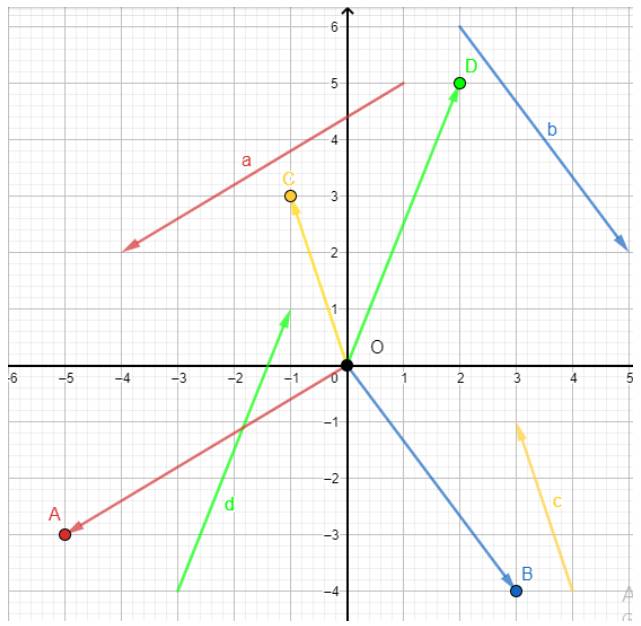
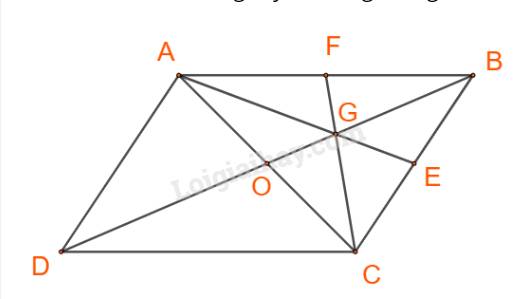
Trong hình 4.27, hãy biểu thị mỗi vecto \(\overrightarrow u ,\;\overrightarrow v \) theo hai vecto \(\overrightarrow a ,\;\overrightarrow b \), tức là tìm các số \(x,y,z,t\) để \(\overrightarrow u = x\overrightarrow a + y\overrightarrow b ,\;\overrightarrow v = t\overrightarrow a + z\overrightarrow b .\).