Question

Answer 1

  

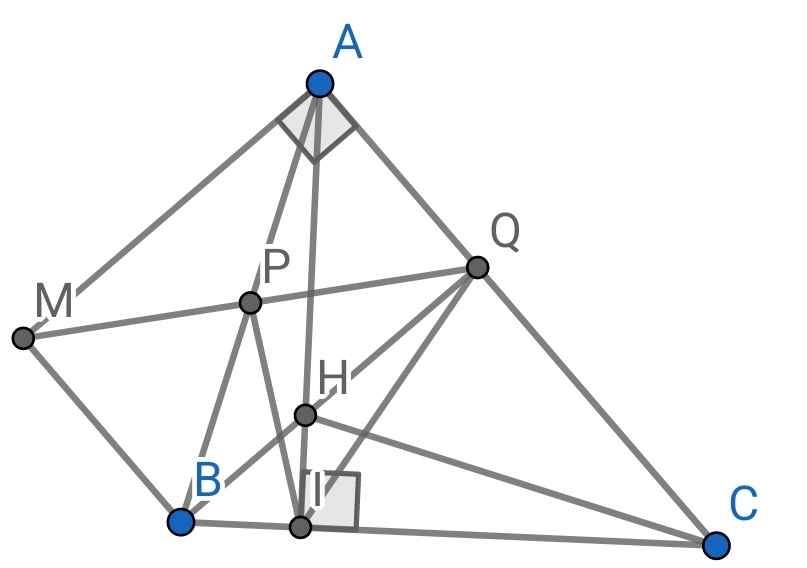
a) Do P là trung điểm của AB (gt)

⇒ PA = PB

Do BM // AC (gt)

⇒ ∠PAQ = ∠PBM (so le trong)

Do AM ⊥ AC (gt)

⇒ AM ⊥ AQ

⇒ ∠MAQ = 90⁰

Xét ∆PAQ và ∆PBM có:

∠PAQ = ∠PBM (cmt)

PA = PB (cmt)

∠APQ = ∠BPM (đối đỉnh)

⇒ ∆PAQ = ∆PBM (g-c-g)

⇒ AQ = BM (hai cạnh tương ứng)

Do BM // AC (gt)

⇒ BM // AQ

Tứ giác AMBQ có:

BM // AQ (cmt)

BM = AQ (cmt)

⇒ AMBQ là hình bình hành

Mà ∠MAQ = 90⁰ (cmt)

⇒ AMBQ là hình chữ nhật

b) Do AMBQ là hình chữ nhật (cmt)

BQ ⊥ AQ

⇒ BQ ⊥ AC

∆ABC có:

BQ ⊥ AC (cmt)

AI ⊥ BC (gt)

⇒ BQ và AI là hai đường cao của ∆ABC

Mà BQ cắt AI tại H (gt)

⇒ CH là đường cao thứ ba của ∆ABC

⇒ CH ⊥ AB

c) Do BQ ⊥ AQ (cmt)

⇒ ∆ABQ vuông tại Q

Mà P là trung điểm của AB (gt)

⇒ QP là đường trung tuyến ứng với cạnh huyền AB của ∆ABC

⇒ QP = AB : 2 (1)

Do AI ⊥ BC (gt)

⇒ ∆ABI vuông tại I

Mà P là trung điểm của AB (gt)

⇒ IP là đường trung tuyến ứng với cạnh huyền AB của ∆ABI

⇒ IP = AB : 2 (2)

Từ (1) và (2) ⇒ QP = IP

⇒ ∆PIQ cân tại P