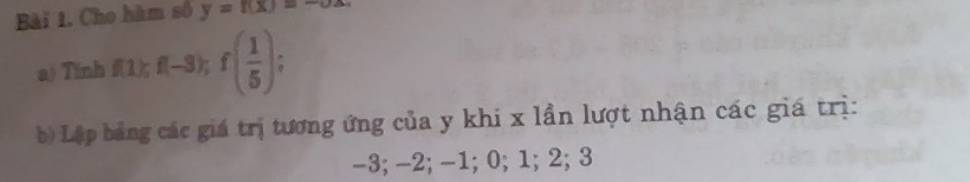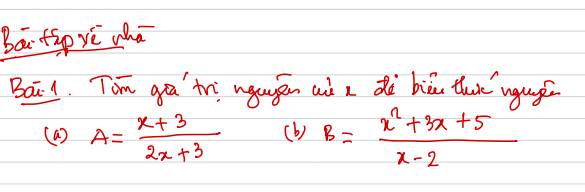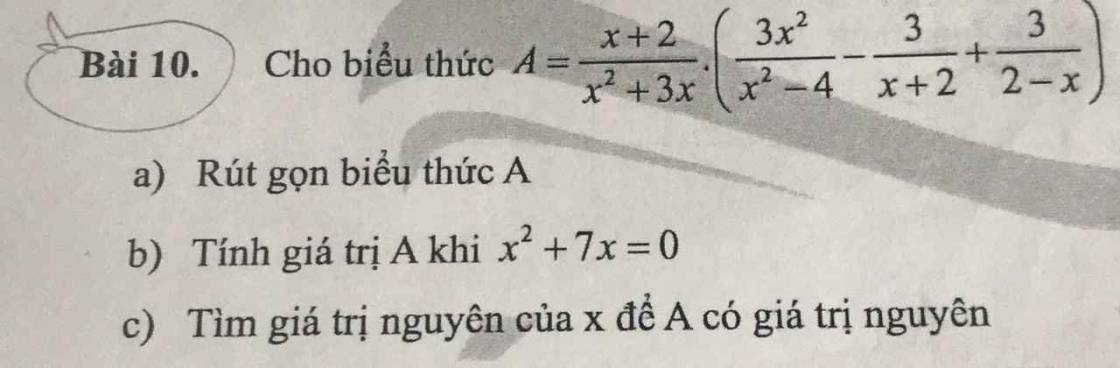Ôn tập: Phân thức đại số

Bài 3:

a: Điểm nằm trên trục tung thì có hoành độ bằng 0

b: Điểm nằm trên trục hoành thì có tung độ bằng 0

Bài 1:f(x)=3x+2

a: Khi x=1 thì \(f\left(1\right)=3\cdot1+2=3+2=5\)

Khi x=-2 thì \(f\left(-2\right)=3\cdot\left(-2\right)+2=-6+2=-4\)

Khi x=1/3 thì \(f\left(\dfrac{1}{3}\right)=3\cdot\dfrac{1}{3}+2=1+2=3\)

b: f(x)=-4

=>3x+2=-4

=>3x=-4-2=-6

=>\(x=-\dfrac{6}{3}=-2\)

Bạn nên gõ hẳn đề bằng công thức toán để mọi người quan sát đề của bạn dễ dàng hơn nhé. Nhìn ntn mờ lắm.

Bài 3:

Nhận xét: M,N,P,Q thẳng hàng

Bạn cần chụp đầy đủ, rõ ràng đề để mọi người hỗ trợ tốt hơn. Đề chụp bị khuyết mất rồi.

a: ĐKXĐ: \(x\notin\left\{-\dfrac{3}{2}\right\}\)

Để A là số nguyên thì \(x+3⋮2x+3\)

=>\(2x+6⋮2x+3\)

=>\(2x+3+3⋮2x+3\)

=>\(3⋮2x+3\)

=>\(2x+3\in\left\{1;-1;3;-3\right\}\)

=>\(2x\in\left\{-2;-4;0;-6\right\}\)

=>\(x\in\left\{-1;-2;0;-3\right\}\)

b: ĐKXĐ: x<>2

Để B là số nguyên thì \(x^2+3x+5⋮x-2\)

=>\(x^2-2x+5x-10+15⋮x-2\)

=>\(15⋮x-2\)

=>\(x-2\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

=>\(x\in\left\{3;1;5;-1;7;-3;17;-13\right\}\)

Lời giải:

$\frac{x^3+8}{x^2-2x+1}.\frac{x^2+3x+2}{1-x^2}=\frac{(x^3+8)(x^2+3x+2)}{(x^2-2x+1)(1-x^2)}$

$=\frac{(x+2)(x^2-2x+4)(x+1)(x+2)}{(x-1)^2(1-x)(x+1)}$

$=\frac{(x+2)^2(x^2-2x+4)}{-(x-1)^3}$
 

1. a) \(7x^2\left(2x^3+3x^5\right)=7x^2\cdot2x^3+7x^2\cdot3x^5=14x^5+21x^7\)

b) \(\left(x^3-x^2+x-1\right):\left(x-1\right)=\dfrac{x^3-x^2+x-1}{x-1}\)

\(=\dfrac{x^2\left(x-1\right)+\left(x-1\right)}{x-1}=\dfrac{\left(x-1\right)\left(x^2+1\right)}{x-1}=x^2+1\)

2: \(x^2-8x+7=0\)

=>\(x^2-x-7x+7=0\)

=>\(x\left(x-1\right)-7\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(x-7\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=7\end{matrix}\right.\)

1:

a: \(7x^2\left(2x^3+3x^5\right)=7x^2\cdot2x^3+7x^2\cdot3x^5=21x^7+14x^5\)

b: \(\dfrac{x^3-x^2+x-1}{x-1}=\dfrac{x^2\left(x-1\right)+\left(x-1\right)}{\left(x-1\right)}\)

\(=x^2+1\)

1)

\(a,7x^2\cdot(2x^3+3x^5)\\=7x^2\cdot2x^3+7x^2\cdot3x^5\\=14x^5+21x^7\\---\\b,(x^3-x^2+x-1):(x-1)(dkxd:x\ne 1)\\=[x^2(x-1)+(x-1)]:(x-1)\\=(x-1)(x^2+1):(x-1)\\=x^2+1\)

2)

\(x^2-8x+7=0\\\Leftrightarrow x^2-x-7x+7=0\\\Leftrightarrow x(x-1)-7(x-1)=0\\\Leftrightarrow (x-1)(x-7)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=7\end{matrix}\right.\)

\(\text{#}Toru\)

a) \(A=\dfrac{x+2}{x^2+3x}\cdot\left(\dfrac{3x^2}{x^2-4}-\dfrac{3}{x+2}+\dfrac{3}{2-x}\right)\) (ĐKXĐ: \(x\ne0;x\ne-3;x\ne\pm2\))

\(=\dfrac{x+2}{x^2+3x}\cdot\left(\dfrac{3x^2}{x^2-4}-\dfrac{3}{x+2}-\dfrac{3}{x-2}\right)\)

\(=\dfrac{x+2}{x^2+3x}\cdot\left[\dfrac{3x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\right]\)

\(=\dfrac{x+2}{x\left(x+3\right)}\cdot\dfrac{3x^2-3x+6-3x-6}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{3x^2-6x}{x\left(x+3\right)\left(x-2\right)}\)

\(=\dfrac{3x\left(x-2\right)}{x\left(x+3\right)\left(x-2\right)}\)

\(=\dfrac{3}{x+3}\)

\(---\)

b) Có: \(x^2+7x=0\)

\(\Leftrightarrow x\left(x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-7\left(tm\right)\end{matrix}\right.\)

Với \(x=-7\), A trở thành:

\(A=\dfrac{3}{-7+3}=-\dfrac{3}{4}\)

\(---\)

c) Để \(A\) có giá trị nguyên thì \(\dfrac{3}{x+3}\) có giá trị nguyên

\(\Rightarrow x+3\inƯ\left(3\right)\)

\(\Rightarrow x+3\in\left\{1;3;-1;-3\right\}\)

\(\Rightarrow x\in\left\{-2;0;-4;-6\right\}\)

Kết hợp với điều kiện xác định của x, ta được: 

\(x\in\left\{-4;-6\right\}\)

Vậy: ...

\(Toru\)

a: s=(2x+5)(x-2)

\(=2x^2-4x+5x-10\)

\(=2x^2+x-10\)

b: Khi x=12 thì \(s=2\cdot12^2+12-10=2\cdot144+2=288+2=290\left(cm^2\right)\)

Nhưng 2 đôi giày này giá mua bằng nhau không nhỉ, nếu bằng thì dễ tính, đủ cơ sở dữ kiện rồi

Giá gốc 2 đôi giày:

19500 : 20% = 97500(đồng)

Giá gốc 1 đôi giày:

97500:2= 48750(đồng)

Đ.số: 48750 đồng

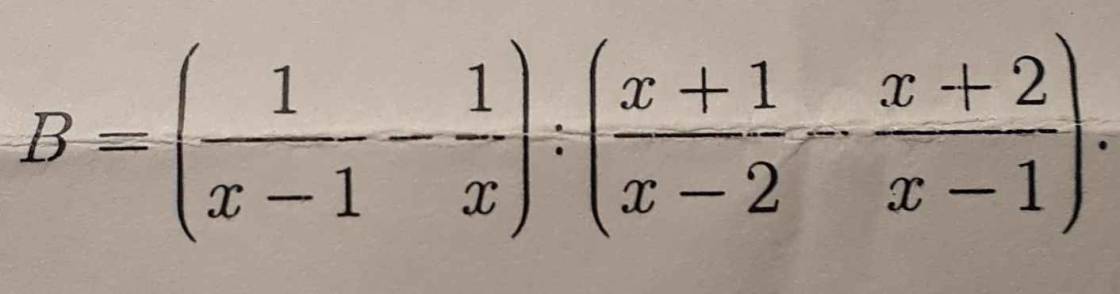
ĐK: \(\left\{{}\begin{matrix}x\ne1\\x\ne0\\x\ne2\end{matrix}\right.\)

Khi đó:

\(B=\left(\dfrac{x}{x\left(x-1\right)}-\dfrac{x-1}{x\left(x-1\right)}\right):\left(\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-2\right)\left(x-1\right)}-\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-1\right)}\right)\\ =\dfrac{1}{x\left(x-1\right)}:\left(\dfrac{x^2-1-x^2+4}{\left(x-2\right)\left(x-1\right)}\right)\\ =\dfrac{1}{x\left(x-1\right)}.\dfrac{\left(x-2\right)\left(x-1\right)}{3}\\ =\dfrac{x-2}{3x}\)

\(B=\left(\dfrac{1}{x-1}-\dfrac{1}{x}\right):\left(\dfrac{x+1}{x-2}-\dfrac{x+2}{x-1}\right)\)

\(=\dfrac{x-x+1}{x\left(x-1\right)}:\dfrac{\left(x+1\right)\left(x-1\right)-\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-1\right)}\)

\(=\dfrac{1}{x\left(x-1\right)}\cdot\dfrac{\left(x-2\right)\left(x-1\right)}{x^2-1-x^2+4}\)

\(=\dfrac{\left(x-2\right)}{3x}\)