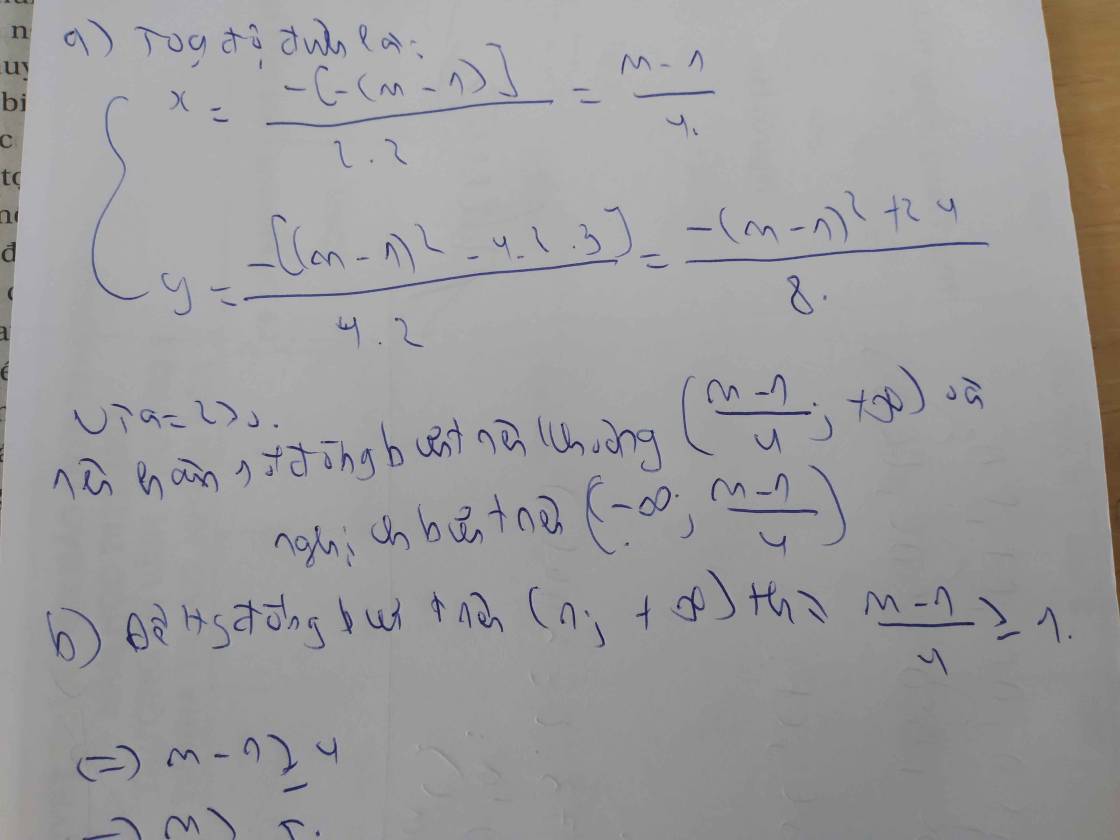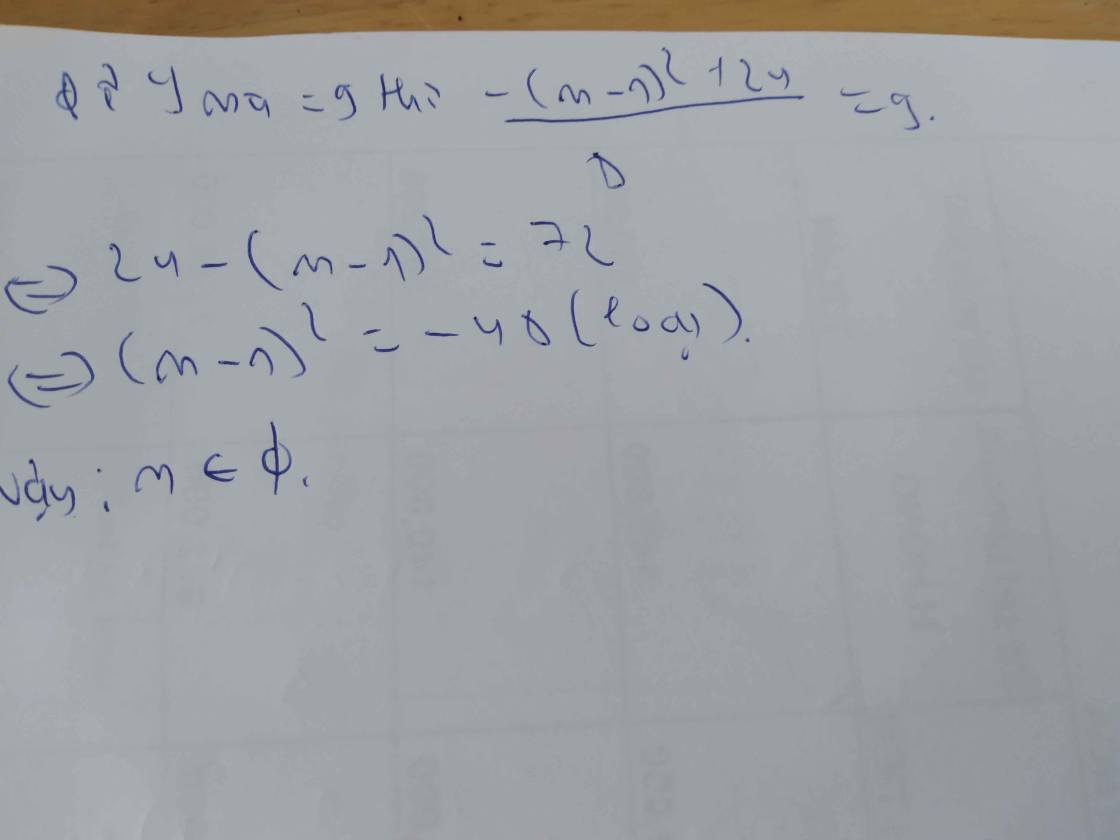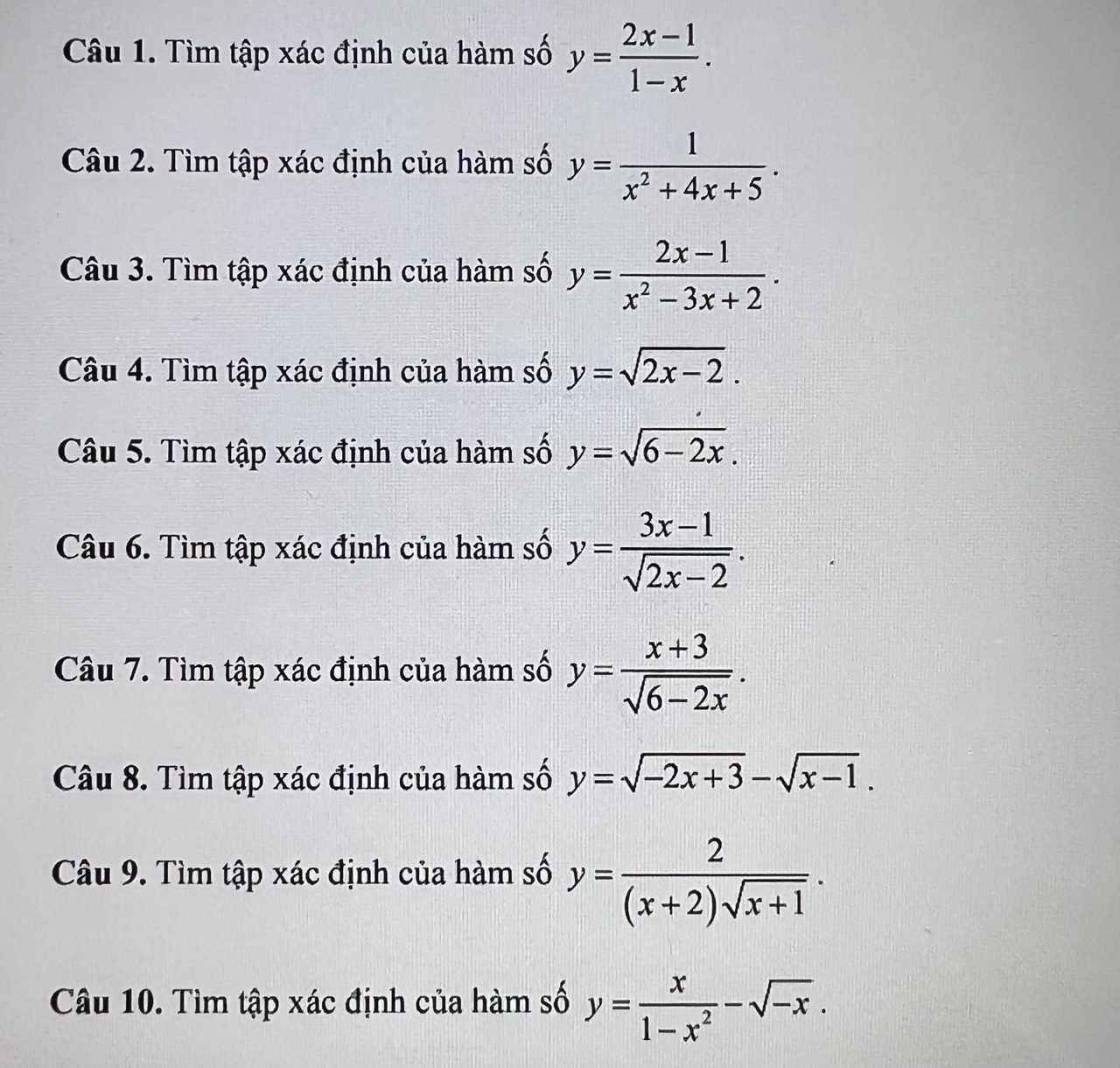Bạn An có 16 cuốn sách 5 sách toán 4 sách lý 7 sách hoá .An lấy ra từ đó 5 cuốn sách có đủ loại sách để tặng cho 5 đứa em .Hỏi an có bảo nhiêu cách tặng sách
Ôn tập cuối năm môn Đại số
Chọn 5 cuốn bất kì từ 16 cuốn và tặng cho 5 em: có \(C_{16}^5=4368\) cách
TH1: trong 5 cuốn sách chỉ có đúng 1 loại sách (5 cuốn toàn toán hoặc toán hóa): \(C_5^5+C_7^5=22\) cách
TH2: 5 cuốn chỉ có đúng 2 loại toán và lý: \(C_9^5-C_5^5=125\) cách
TH3: 5 cuốn chỉ có đúng 2 loại toán và hóa: \(C_{12}^5-\left(C_5^5+C_7^5\right)=770\)
TH4: 5 cuốn chỉ có đúng 2 loại lý và hóa: \(C_{11}^5-C_7^5=441\) cách
\(\Rightarrow\) Số cách để chọn 5 cuốn có đủ loại sách là:
\(4368-\left(22+125+770+441\right)=3010\) (cách)
Đem 5 cuốn đó tặng cho 5 em: có \(3010.5!=...\) cách
Đúng 2
Bình luận (0)
Một đội bóng mềm bảo trợ cho 1 chuyến đi xem 1 trận bóng chày chuyên nghiệp để gây quỹ. Họ thuê 1 xe 60 chỗ với giá 5 250 000 đồng. Để kiếm được lợi nhuận cao, họ tính phí 150 000 đồng cho mỗi người nếu bán hết tất cả các chôc trên xe. Cứ mỗi ghế trống, họ sẽ tăng giá 15 000 đồng trên một người. Tìm lợi nhuận nhiều nhất và cần bao nhiêu khách để thu được lợi nhuận nhiều nhất.
Đọc tiếp
Một đội bóng mềm bảo trợ cho 1 chuyến đi xem 1 trận bóng chày chuyên nghiệp để gây quỹ. Họ thuê 1 xe 60 chỗ với giá 5 250 000 đồng. Để kiếm được lợi nhuận cao, họ tính phí 150 000 đồng cho mỗi người nếu bán hết tất cả các chôc trên xe. Cứ mỗi ghế trống, họ sẽ tăng giá 15 000 đồng trên một người. Tìm lợi nhuận nhiều nhất và cần bao nhiêu khách để thu được lợi nhuận nhiều nhất.
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
Chứng minh rằng sin A x sin B + sin B x sin C + sin C x sin A =\(\dfrac{\text{ r^2 + p^2+4Rr
}}{\text{ 4R^2
}}\)với R, r lần lượt là bán kính đường trọn ngoại tiếp và bán kính đường tròn nội tiếp △ABC
Xem chi tiết
Ta có:
\(r^2+p^2+4Rr=\left(\dfrac{S}{p}\right)^2+p^2+\dfrac{abc}{S}.\dfrac{S}{p}\)
\(=\dfrac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}+p^2+\dfrac{abc}{p}\)
\(=\dfrac{p^3+\left(ab+bc+ac\right)p-p^2\left(a+b+c\right)-abc+p^3+abc}{p}\)
\(=ab+bc+ca\)
Do đó:
\(\dfrac{ab+bc+ca}{4R^2}=\dfrac{r^2+p^2+4Rr}{4R^2}\)
\(\Leftrightarrow sinAsinB+sinBsinC+sinCsinA=\dfrac{r^2+p^2+4Rr}{4R^2}\)\(\left(đpcm\right)\)
Đúng 1
Bình luận (1)
bạn giải thích chi tiết đoạn này hộ mình được ko ạ
p^3+(ab+bc+ac)p−p^2(a+b+c)−abc+p^3+abc/p =ab+bc+ca
Đúng 0
Bình luận (2)
Có bao nhiêu cách xếp số 7 và 8 vào tập hợp gồm n phần tử?
Ví dụ: n = 2
[7,7], [7,8], [8,7], [8,8]
Có 2 cách xếp số 7 và 8 vào tập hợp gồm n = 2 phần tử.
Đó là: {7; 8} ; {8; 7}
Đúng 0
Bình luận (0)
1:
ĐKXĐ: 1-x<>0
=>x<>1
Vậy: TXĐ: D=R\{1}
2: ĐKXĐ: x^2+4x+5<>0
=>x thuộc R
=>TXĐ là D=R
3: ĐKXĐ: x^2-3x+2<>0
=>(x-1)(x-2)<>0
=>x<>1 và x<>2
=>TXĐ: D=R\{1;2}
4: ĐKXĐ: 2x-2>=0
=>x>=1
=>TXĐ: D=[1;+vô cực)
5: ĐKXĐ: 6-2x>=0
=>x<=3
TXĐ: D=(-vô cực;3]
6: ĐKXĐ: 2x-2>0
=>x>1
TXĐ: D=(1;+vô cực)
7: ĐKXĐ: 6-2x>0
=>x<3
TXĐ: D=(-vô cực;3)
8: ĐKXĐ: -2x+3>=0 và x-1>=0
=>x<=3/2 và x>=1
=>D=[1;3/2]
9: ĐKXĐ: (x+2)*căn x+1<>0
=>x+1>0 và x+2<>0
=>x>-1
=>D=(-1;+vô cực)
10: ĐKXĐ: x>=0 và 1-x^2<>0
=>x>=0 và x<>1;x<>-1
=>TXĐ: D=[0;+vô cực]\{1}
Đúng 0
Bình luận (0)
Một mật khẩu có 6 kí tự; trong đó kí tự ở vị trí đầu tiên là một chữ cái A HOẶC B; kí tự ở vị trí thứ hai là một chữ số thuộc tập {1;2;3;..;9}; mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập {0;1;2;3..9}. Hỏi có thể làm được nhiều nhất bao nhiêu mật khẩu khác nhau?
Số mật khẩu có thể lập được là:
\(2\cdot9\cdot C^4_{10}=3780\left(cái\right)\)
Đúng 0
Bình luận (0)
Ta có: \(\overline{abcdef}\) là số mật khẩu
a có 2 cách chọn : \(C_2^1\)
b có 9 cách chọn : \(C_9^1\)
c,d,e,f có 10 cách chọn : \(C_{10}^4\)
=> số cách chọn là : 2 . 9 . 210 = 3780 ( mật khẩu )
Đúng 0
Bình luận (0)
Gieo 1 con xúc xắc cân đối đồng chất. Giả sử con xúc xắc xuất hiện mặt \(b\) chấm. Tính xác suất để phương trình: \(x^2+bx+2=0\) vô nghiệm.
Δ=b^2-4*1*2=b^2-8
Để phương trình vô nghiệm thì b^2-8<0
=>-2 căn 2<b<2 căn 2
=>b=1 hoặc b=2
Đúng 0
Bình luận (0)
Cho \(n\in N^{sao}\) thỏa \(C_n^1+C_n^2=15.\) Tìm số hạng không chứa \(x\) trong khai triển \(\left(x+\dfrac{2}{x^4}\right)^n\)
\(C^1_n+C^2_n=15\) (Điều kiện: \(n\ge2\))
\(\Leftrightarrow n+\dfrac{n!}{2!\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)\left(n-2\right)!}{2\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)}{2}=15\)
\(\Leftrightarrow2n+n\left(n-1\right)=30\)
\(\Leftrightarrow2n+n^2-n=30\)
\(\Leftrightarrow n^2+n-30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=5\\n=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{2}{x^4}\right)^5=C^k_5x^{5-k}\left(\dfrac{2}{x^4}\right)^k=C^k_5x^{5-k-4k}.2^k=C^k_5x^{5-5k}.2^k\)
\(ycbt\Leftrightarrow5-5k=0\Leftrightarrow k=1\)
\(\Rightarrow C^1_5.2^1=10\)
Vậy số hạng không chứa \(x\) trong khai triển là \(10\).
Đúng 0
Bình luận (0)
Tìm số hạng không chứ \(x\) trong khai triển \(\left(2x^2-\dfrac{1}{x^2}\right)^4\) \(\left(x\ne0\right)\)
\(\left(2x^2-\dfrac{1}{x^2}\right)^4=C^k_4\left(2x^2\right)^{4-k}\left(-\dfrac{1}{x^2}\right)^k\)
\(=C^k_4.2^{4-k}.x^{8-2k-2k}.\left(-1\right)^k\)
\(=C^k_4.2^{4-k}.x^{8-4k}.\left(-1\right)^k\)
\(ycbt\Leftrightarrow8-4k=0\Leftrightarrow k=2\)
\(\Rightarrow C^2_4.2^{4-2}.\left(-1\right)^2=24\)
Vậy số hạng không chứa \(x\) trong khai triển là \(24\).
Đúng 0
Bình luận (0)