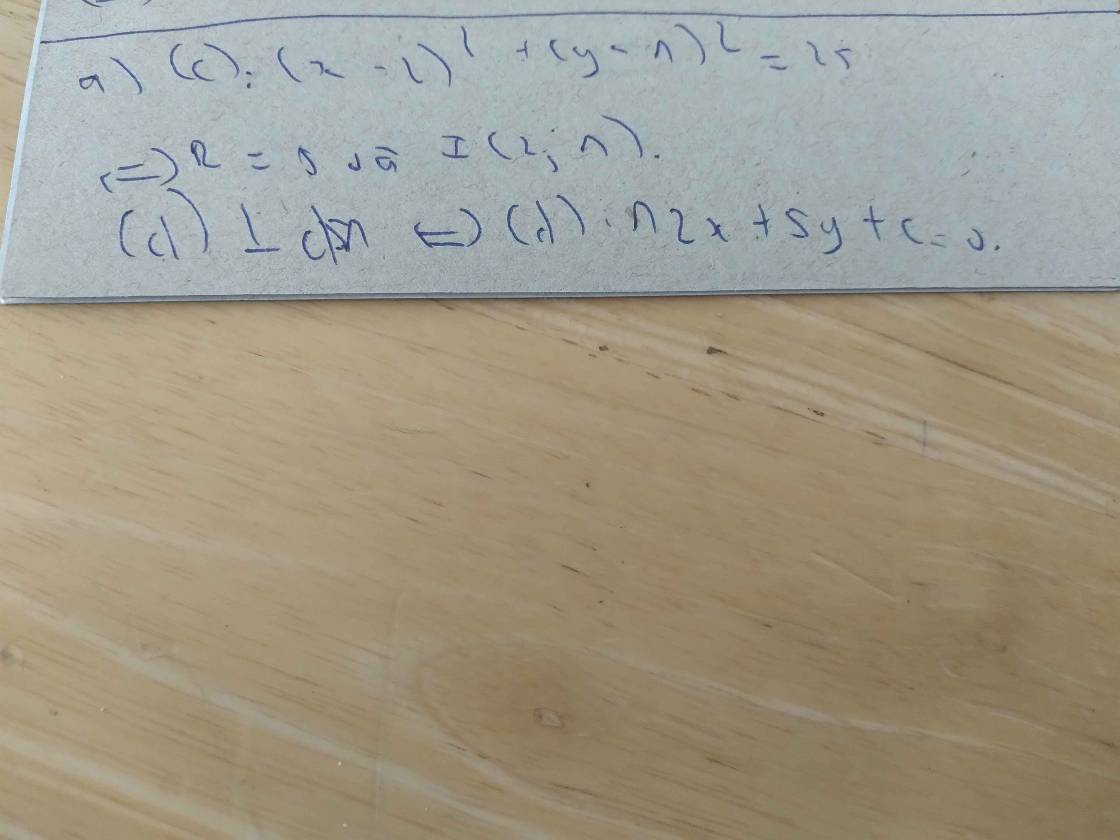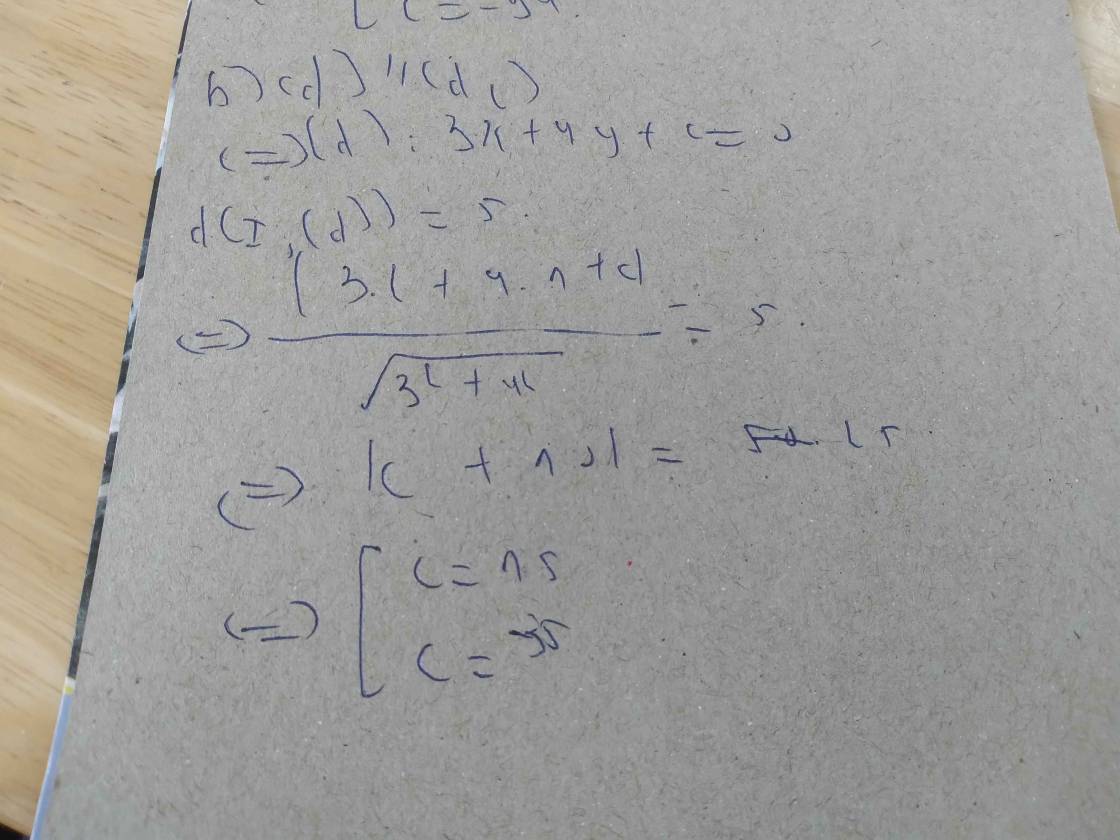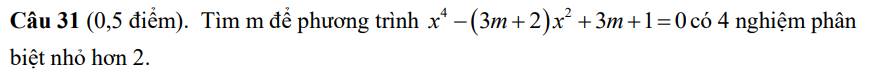viết phương trình chính tắc của elip các trường hợp sau 1. elip đi qua điểm M(0;3) và có tiêu điểm F2(5;0) 2. Elip đi qua hai điểm A(7;0), B(0;3) 3. Elip đi qua hai điểm A(0;1), N(1; căn 3 / 2)
Ôn tập cuối năm môn Đại số
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
Đúng 2
Bình luận (0)
gieo một con xúc xắc hai lần liên tiếp. tính xác suất trong các trường hợp a. lần gieo thứ nhất xuất hiện mặt một chấm b. tổng số chấm hai lần gieo bằng 5 c. hiệu số chấm hai lần gieo bằng 2 d. tích số chấm hai lần gieo là một số lẻ e. tổng số chấm hai lần gieo là một số chia hết cho 3
a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4
Đúng 1
Bình luận (0)
gieo ngẫu nhiên một đồng xu 3 lần liên tiếp. Tính xác suất của các biến cố sau: A:" Ba lần gieo xuất hiện như nhau" B:" mặt ngửa xuất hiện đúng một lần" C: "lần thứ hai xuất hiện mặt sấp" D:"mặt ngửa xuất hiện ít nhất một lần"
a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4
Đúng 2
Bình luận (0)
a, cho elip (E) có phương trình chính tắc x^2/49+y^2/25=1. tìm toạ độ các giao điểm của (E) với các trục ox,oy và toạ độ các tiêu điểm của (E)
cho đường tròn (c): (x-2)^2+(y-1)^2=25. viết phương trình tiếp tuyến của (c) trong các trường hợp sau: a, tiếp tuyến vuông góc với đường thẳng d1: 5x-12y+2=0 b, tiếp tuyến song song với d2: 3x+4y+2=0 c, tiếp tuyến qua điểm A(3;6)
một nhóm có 5 học sinh nam và 6 học sinh nữ. Hỏi có bao nhiêu cách xếp các học sinh thành một hàng ngang sao cho các học sinh cùng giới ngồi cạnh nhau. Học sinh nam và nữ ngồi xen kẽ. Các học sinh nam không ngồi cạnh nhau
a: SỐ cách xếp là;
5!*6!*2=172800(cách)
b: Số cách xếp là \(6!\cdot5!=86400\left(cách\right)\)
Đúng 0
Bình luận (0)
một hộp có 12 viên bi, trong đó có 5 viên bi vàng, 3 viên bi xanh và 4 viên bi đỏ. có bao nhiêu cách để chọn ra 4 viên bi có ít nhất 1 viên bi xanh
Số cách lấy ra là:
\(C^1_3\cdot C^3_9+C^2_3\cdot C^2_9+C^3_3\cdot C^1_9=369\left(cách\right)\)
Đúng 1
Bình luận (1)
tìm xác xuất để 2 người gặp ngẫu nhiên ngoài đường trùng sinh nhâtj nhau . giả sử 1 năm 365
Không gian mẫu: \(365.365=365^2\)
Người thứ nhất có 365 khả năng ngày sinh, người thứ 2 chỉ có 1 khả năng trùng với người thứ nhất nên có \(365.1=365\) khả năng 2 người trùng ngày sinh
Xác suất: \(P=\dfrac{365}{365^2}=\dfrac{1}{365}\)
Đúng 0
Bình luận (0)
Đặt x^2=t
=>t^2-(3m+2)t+3m+1=0(2)
Để (1) có 4 no pb nhỏ 2 thì (2) phải có 2 nghiệm dương phân biệt nhỏ hơn 4
=>(3m+2)^2-4(3m+1)>0 và 0<3m+1<4 và 3m+1>0
=>m<>0 và -1/3<m<1
Đúng 0
Bình luận (0)
a: vecto AB=(4;-3)
Phương trình tham số là x=1+4t và y=2-3t
b: Phương trình đường cao đi qua C là:
4(x-0)+(-3)(y-4)=0
=>4x-3y+12=0
c: Gọi (C): x^2+y^2-2ax-2by+c=0 là phương trình đường tròn ngoại tiếp ΔABC
Theo đề, ta có:
1^2+2^2-2a-4b+c=0 và 25+1-10a+2b+c=0 và 0^2+4^2-2a*0-2b*4+c=0
=>-2a-4b+c=-5 và -10a+2b+c=-26 và -8b+c=-16
=>a=15/2; b=13/2; c=36
=>x^2+y^2-15x-13y+36=0
=>x^2-15x+56,25+y^2-13y+42,25=62,5
=>(x-7,5)^2+(y-6,5)^2=62,5
=>R=căn 62,5 và I(7,5;6,5)
Đúng 0
Bình luận (0)