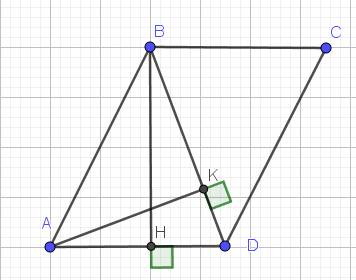
Lời giải:
a. Kẻ $BH\perp AD$.
Có: $\frac{BH}{AB}=\sin A=\sin 60^0=\frac{\sqrt{3}}{2}$
$BH=AB.\frac{\sqrt{3}}{2}=\frac{5}{2}\sqrt{3}$
$S_{ABCD}=BH.AD=\frac{5}{2}\sqrt{3}.4=10\sqrt{3}$ (cm2)
b.
$AH=AB\cos A=5\cos 60^0=\frac{5}{2}$ (cm)
$HD=AD-AH=4-\frac{5}{2}=1,5$ (cm)
$\tan \widehat{BDA}=\tan \widehat{BDH}=\frac{BH}{HD}=\frac{5}{2}\sqrt{3}: 1,5=\frac{5\sqrt{3}}{3}$
$\Rightarrow \widehat{BDA}=70,9^0$
$\widehat{ABK}=\widehat{ABD}=180^0-\widehat{BAD}-\widehat{BDA}=180^0-60^0-70,9^0=49,1^0$
$AK=AB\sin \widehat{ABK}=5\sin 49,1^0=3,8$ (cm)
Đúng 0
Bình luận (1)