Ôn tập chương 2: Hàm số bậc nhất

Đồ thị \(y=-x+2\) đi qua 2 điểm \(C\left(0;2\right);D\left(2;0\right)\) vì 

\(\left\{{}\begin{matrix}2=0+2\\0=-2+2\end{matrix}\right.\left(đúng\right)\)

Vậy chọn câu C và D

\(\left\{{}\begin{matrix}\left(d_1\right):y=3x-1\\\left(d_2\right):y=-x+\left(m+2\right)\end{matrix}\right.\)

Theo đề bài ta có :

\(\left(d_1\right)\cap\left(d_2\right)=A\left(0;y\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=3.0-1=-1\\0+m+2=-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\m=-3\end{matrix}\right.\) Nên chọn câu B

Hàm số y=(a+1)x-2 đồng biến khi a+1>0

=>a>-1

1) \(\left\{{}\begin{matrix}\left(d_1\right):y=2x\\\left(d_2\right):y=-\dfrac{1}{2}x+5\end{matrix}\right.\)

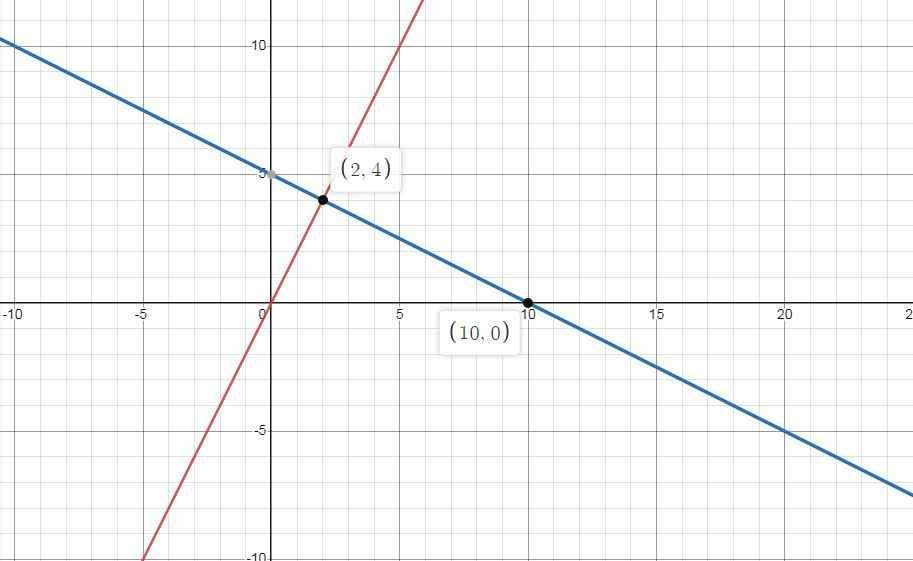
2) Theo đồ thi ta có :

\(\left(d_1\right)\cap\left(d_2\right)=A\left(2;4\right)\)

3) \(\left(d_2\right)\cap Ox=B\left(a;0\right)\)

\(\Leftrightarrow-\dfrac{1}{2}a+5=0\)

\(\Leftrightarrow\dfrac{1}{2}a=5\)

\(\Leftrightarrow a=10\)

\(\Rightarrow\left(d_2\right)\cap Ox=B\left(10;0\right)\)

4) \(OA=\sqrt[]{\left(2-0\right)^2+\left(4-0\right)^2}=\sqrt[]{20}=2\sqrt[]{5}\)

   \(OB=\sqrt[]{\left(10-0\right)^2+\left(0-0\right)^2}=\sqrt[]{10^2}=10\)

  \(AB=\sqrt[]{\left(10-2\right)^2+\left(0-4\right)^2}=\sqrt[]{80}=4\sqrt[]{5}\)

Ta thấy :

 \(OA^2+AB^2=20+80=OB^2=100\)

\(\Rightarrow\Delta OAB\) vuông tại A

\(\Rightarrow\widehat{OAB}=90^o\)

\(sin\widehat{AOB}=\dfrac{AB}{OB}=\dfrac{4\sqrt[]{5}}{10}=\dfrac{2\sqrt[]{5}}{5}\)

\(\Rightarrow\widehat{AOB}\sim63,43^o\)

\(\Rightarrow\widehat{OBA}=90^o-63,43^o=26,57^o\)

5) Chu vi \(\Delta OAB\) :

\(AB+OA+OB=4\sqrt[]{5}+2\sqrt[]{5}+10=10\sqrt[]{5}+10=10\left(\sqrt[]{5}+1\right)\left(đvmd\right)\)

Diện tích \(\Delta OAB\) :

\(\dfrac{1}{2}AB.OA=\dfrac{1}{2}.4\sqrt[]{5}.2\sqrt[]{5}=20\left(đvdt\right)\)

Tọa độ A là;

\(\left\{{}\begin{matrix}y=0\\\left(m+1\right)x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{m+1}\\y=0\end{matrix}\right.\Leftrightarrow OA=\dfrac{3}{\left|m+1\right|}\)

Tọa độ B là:

x=0 và y=(m+1)*0+3=3

=>OB=3

S_OAB=9

=>1/2*OA*OB=9

=>1/2*9/|m+1|=9

=>1/2*1/|m+1|=1

=>1/|m+1|=2

=>|m+1|=1/2

=>m+1=1/2 hoặc m+1=-1/2

=>m=-1/2 hoặc m=-3/2

b: Để (d)//y=-3x+2 thì m-1=-3

=>m=-2

c:

PTHĐGĐ là:

(m-1)x-4=x-7

=>(m-2)x=-3

Để hai đường cắt nhau tại một điểm nằm bên trái trục tung thì m-1<>1 và -3/(m-2)<0

=>m<>2 và m-2>0

=>m>2

Gọi vận tốc xe 1 là x

Vận tốc xe 2 là x+10

Theo đề, ta có: 2(x+x+10)=120

=>2x+10=60

=>2x=50

=>x=25

Vận tốc xe 2 là 25+10=35km/h

Đặt gốc tọa độ tại điểm khởi hành của xe 1, chiều dương là từ vị trí khởi hành của xe 1 đến vị trí khởi hành của xe 2

Phương trình quãng đường xe 1 :

\(x_1=v_1t\)

Phương trình quãng đường xe 2 :

\(x_2=120-v_2t\)

Để 2 xe gặp nhau khi vầ chỉ khi

\(x_1=x_2\)

\(\Leftrightarrow v_1t=120-v_2t\)

\(\Leftrightarrow\left(v_1+v_2\right)t=120\)

\(\Leftrightarrow v_1+v_2=\dfrac{120}{t}\)

\(\Leftrightarrow v_1+v_2=\dfrac{120}{2}=60\left(t=2\right)\)

mà \(v_2-v_1=10\)

\(\Leftrightarrow\left\{{}\begin{matrix}v_1=\dfrac{60-10}{2}=25\\v_2=60-25=35\end{matrix}\right.\)

\(\)Vậy vận tốc xe 1 là \(25\left(km\right)\)/\(h\); vận tốc xe 2 là \(35km\)/\(h\)

Gọi thời gian hoàn thành công việc khi làm một mình của tổ 1 và tổ 2 lần lượt là a,b

Trong 1h, tổ 1 làm được 1/a(công việc)

Trong 1h, tổ 2 làm được 1/b(công việc)

Theo đề, ta có hệ:

1/a+1/b=1/15 và 3/a+5/b=1/4

=>3/a+3/b=1/5 và 3/a+5/b=1/4

=>-2/b=-1/20 và 1/a+1/b=1/15

=>b=40 và 1/a=1/15-1/40=8/120-3/120=5/120=1/24

=>a=24 và b=40

1: mx+y=2m+2 và x+my=11

Khi m=-3 thì hệ sẽ là:

-3x+y=-6+2=-4 và x-3y=11

=>-3x+y=-4 và 3x-9y=33

=>-8y=29 và 3x-y=4

=>y=-29/8 và 3x=y+4=3/8

=>x=1/8 và y=-29/8

2: Để hệ có 1 nghiệm duy nhất thì \(\dfrac{m}{1}< >\dfrac{1}{m}\)

=>m^2<>1

=>m<>1 và m<>-1

Để hệ vô số nghiệm thì \(\dfrac{m}{1}=\dfrac{1}{m}=\dfrac{2m+2}{11}\)

=>(m=1 hoặc m=-1) và (11m=2m+2)

=>\(m\in\varnothing\)

Để hệ vô nghiệm thì m/1=1/m<>(2m+2)/11

=>m=1 hoặc m=-1

1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3

a: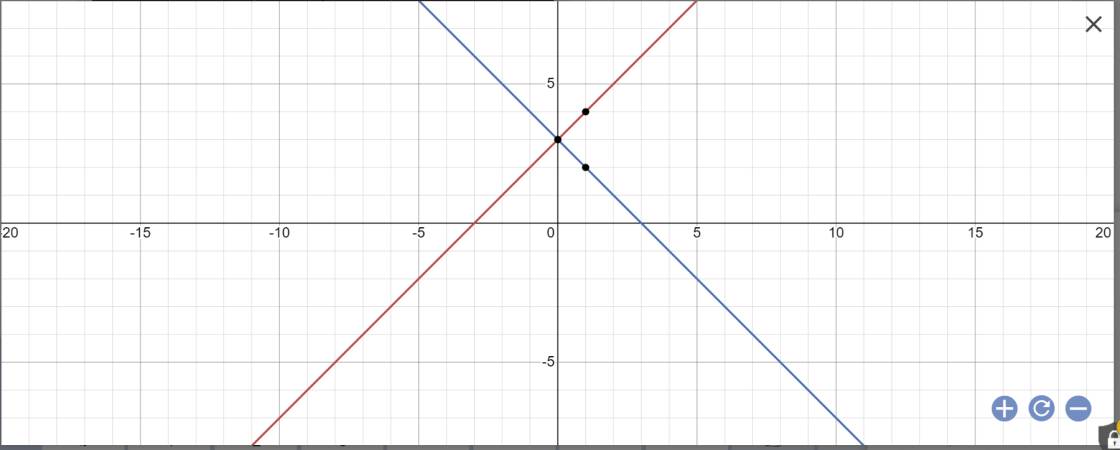 

b: Tọa độ giao điểm là:

x+3=-x+3 và y=x+3

=>x=0 và y=3