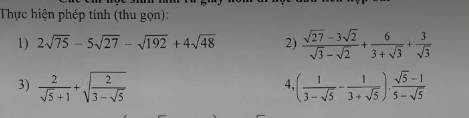
ai giup mik dc ko a mik cam on truoc
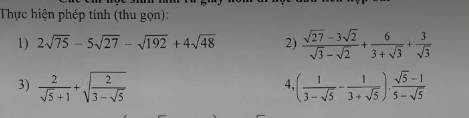
ai giup mik dc ko a mik cam on truoc
1: \(2\sqrt{75}-5\sqrt{27}-\sqrt{192}+4\sqrt{48}\)
\(=2\cdot5\sqrt{3}-5\cdot3\sqrt{3}-8\sqrt{3}+4\cdot4\sqrt{3}\)
\(=10\sqrt{3}-15\sqrt{3}-8\sqrt{3}+16\sqrt{3}\)
\(=3\sqrt{3}\)
2: \(\dfrac{\sqrt{27}-3\sqrt{2}}{\sqrt{3}-\sqrt{2}}+\dfrac{6}{3+\sqrt{3}}+\dfrac{3}{\sqrt{3}}\)
\(=\dfrac{3\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}+\dfrac{6\left(3-\sqrt{3}\right)}{9-3}+\sqrt{3}\)
\(=3+3-\sqrt{3}+\sqrt{3}=6\)
3: \(\dfrac{2}{\sqrt{5}+1}+\sqrt{\dfrac{2}{3-\sqrt{5}}}\)
\(=\dfrac{2\left(\sqrt{5}-1\right)}{5-1}+\sqrt{\dfrac{2\left(3+\sqrt{5}\right)}{4}}\)
\(=\dfrac{\sqrt{5}-1}{2}+\sqrt{\dfrac{6+2\sqrt{5}}{4}}\)
\(=\dfrac{\sqrt{5}-1}{2}+\dfrac{\sqrt{5}+1}{2}=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
4: \(\left(\dfrac{1}{3-\sqrt{5}}-\dfrac{1}{3+\sqrt{5}}\right)\cdot\dfrac{\sqrt{5}-1}{5-\sqrt{5}}\)
\(=\dfrac{3+\sqrt{5}-3+\sqrt{5}}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\cdot\dfrac{\sqrt{5}-1}{\sqrt{5}\left(\sqrt{5}-1\right)}\)
\(=\dfrac{2\sqrt{5}}{9-5}\cdot\dfrac{1}{\sqrt{5}}=\dfrac{2}{4}=\dfrac{1}{2}\)
Hàm số là hai đường thẳng d y=(m+2)-m ; d' y=-2x -2m +1 Tìm giá trị của m để d ,d' cắt nhau Hàm số sau trên cùng một đoạn thẳng. y=3x Y=1,5x Y=-2x+6
a:
Sửa đề: d: y=(m+2)x-m; d': y=-2x-2m+1
Để d và d' cắt nhau thì \(m+2\ne-2\)
=>\(m\ne-4\)
Cho 3 điểm A(-1;6) , B(-4;4) , C(1;1) tìm tọa độ đỉnh D của hình bình hành
A(-1;6); B(-4;4); C(1;1); D(x;y)
Tọa độ của vecto AB là:
\(\left\{{}\begin{matrix}x=-4-\left(-1\right)=-4+1=-3\\y=4-6=-2\end{matrix}\right.\)
Tọa độ của vecto DC là:
\(\left\{{}\begin{matrix}x_{DC}=1-x\\y_{DC}=1-y\end{matrix}\right.\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
mà \(\overrightarrow{AB}=\left(-3;-2\right)\)
và \(\overrightarrow{DC}=\left(1-x;1-y\right)\)
nên \(\left\{{}\begin{matrix}1-x=-3\\1-y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Vậy: D(4;3)
Cho hai hàm số y = 4x + 2 (1)và hàm số y = 2x - 2(2)câu a vẽ đồ thị câu b tìm tọa độ giao điểm m của hai hàm số trên câu c tìm tọa độ a b là giao điểm của hai đồ thị hàm số 1 2 với trục ox câu d tính chu vi diện tích tam giác MAB + e tính các góc của tam giác MAB
a:
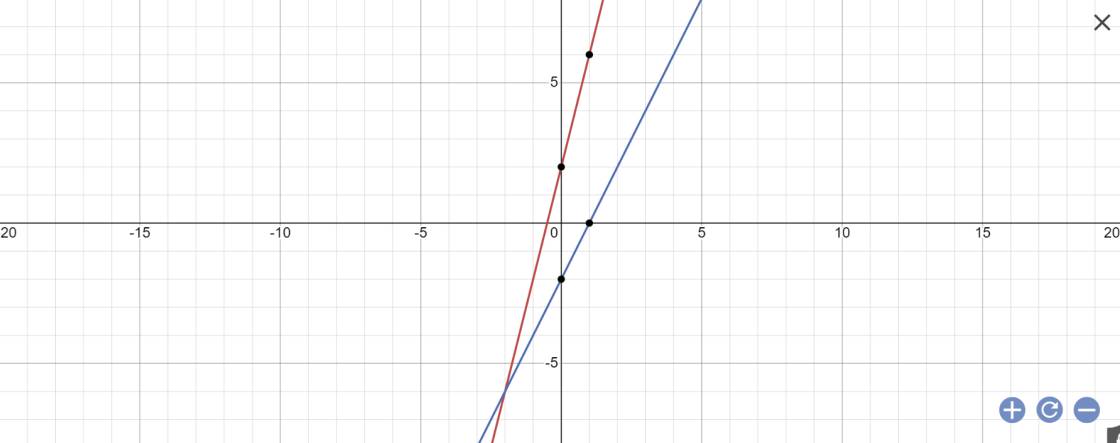
b: phương trình hoành độ giao điểm là:
4x+2=2x-2
=>4x-2x=-2-2
=>2x=-4
=>x=-2
Thay x=-2 vào y=4x+2, ta được:
\(y=4\cdot\left(-2\right)+2=-8+2=-6\)
Vậy: M(-2;-6)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\4x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\4x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Vậy: B(1;0); A(-1/2;0)
d: M(-2;-6); B(1;0); A(-1/2;0)
\(MA=\sqrt{\left(-\dfrac{1}{2}+2\right)^2+\left(0-6\right)^2}=\dfrac{3\sqrt{17}}{2}\)
\(MB=\sqrt{\left(1+2\right)^2+\left(0+6\right)^2}=3\sqrt{5}\)
\(AB=\sqrt{\left(-\dfrac{1}{2}-1\right)^2+\left(0-0\right)^2}=\dfrac{3}{2}\)
Chu vi tam giác MAB là:
\(C_{MAB}=MA+MB+AB=\dfrac{3}{2}+3\sqrt{5}+\dfrac{3\sqrt{17}}{2}\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{9}{\sqrt{85}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{9}{\sqrt{85}}\right)^2}=\dfrac{2}{\sqrt{85}}\)
Diện tích tam giác MAB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{17}}{2}\cdot3\sqrt{5}\cdot\dfrac{2}{\sqrt{85}}\)
\(=\dfrac{9}{2}\)
Ngày đầu tiên lên cấp hai , ai cũng được gặp giáo viên chủ nhiệm mới. Lên cấp hai nhà trường thông báo:"chủ nhiệm lớp sáu A năm nay là giáo viên mới chuyển tới, là cô giáo Hà Thị Huyền Trang" , lúc đó tôi vẫn bận kết bạn mới nên không nghe rõ nên không biết chủ nhiệm là ai . Lúc này bỗng một người phụ nữ mặc áo dài lộng lẫy đi tới dắt tay tôi vào lớp, cô giới thiệu : " bây giờ cô là chủ nhiệm lớp em , tên cô là Hà Thị Huyền Trang , từ hôm nay cô sẽ là chủ nhiệm lớp em đến hết lớp chín", tôi thấy ấm áp lắm , dọng nói hiền từ và đầy cảm súc đã dẫn bước tôi hết năm lớp sáu.
Đầu năm lớp sáu , nhà trường đưa đến cho chúng tôi một món quà chính là cô giáo Hà Thị Huyền Trang , cô giáo nhìn rất trẻ trung và xinh đẹp được biết cô là cô giáo mới đi dậy và đây là năm dậy đầu tiên của cô ở trường tôi.Lúc đầu khi tôi bước chân vào lớp thì tôi rất bỡ ngỡ và biết rất ít người quen , lúc đó các bạn còn chia bè phái trường tiểu học Phượng Vĩ một và trường tiểu học Phượng Vĩ hai nữa cơ , nhưng lúc này cô xuất hiện như một vị cứu tinh , giảng hòa và động viên các bạn hãy kết bạn với nhau .Sau một thời gian các đã đoàn kết hơn , thoải mái hơn với nhau và tôi cũng biết chắc chắn đó là do cô mang đến.Cô hiền hậu dìu dắt chúng tôi trong năm học để được kết quả cao trong học tập , chỗ nào không hiểu có cô lo , chỗ nào không biết có cô dạy , tôi bị bắt nạt có cô giải vây . Cuối cùng sau bao nhiêu năm tháng vất vả rèn luyện lớp chúng tôi nhờ sự dìu dắt của cô đã có kết quả tốt, các bạn đi thi học sinh năng khiếu được điểm cao , lớp có hơn một phần ba là học sinh giỏi , còn lại gần như là học sinh khá giỏi hết.Cô thật hiền từ cuối năm ăn mừng cô đã không ngại bỏ thêm tiền để cho học sinh liên hoan thoải mái hơn , "em cảm ơn cô".
-"Em cảm ơn cô , cảm ơn cô rất nhiều , cô đã dìu dắt em suốt khoảng thời gian qua , cô thật tuyệt vời , cô như ánh nắng ban mai , cô lộng lẫy đẹp hơn tất cả , trong tim em cô là người mẹ thứ hai , em không kìm được tặng cô một bài thơ":
" Người lái đò ơn không kể hết
Tay dắt tay uấn lại nết em
Nước dâng lên ngày cô dìu dắt
Chân trên đất em cảm ơn cô"
Bài II (2.5 điểm): Cho hàm số bậc nhất y = (m - 1) x +m có đồ thị là đường thẳng (d) với m khác 1
1. Với m=2, vẽ đồ thị hàm số và tính số đo góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến độ)
2. Tìm m để đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 1
3. Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của m
Em cần gấp ạ
1: Khi m=2 thì y=(2-1)x+2=x+2
Vẽ đồ thị:
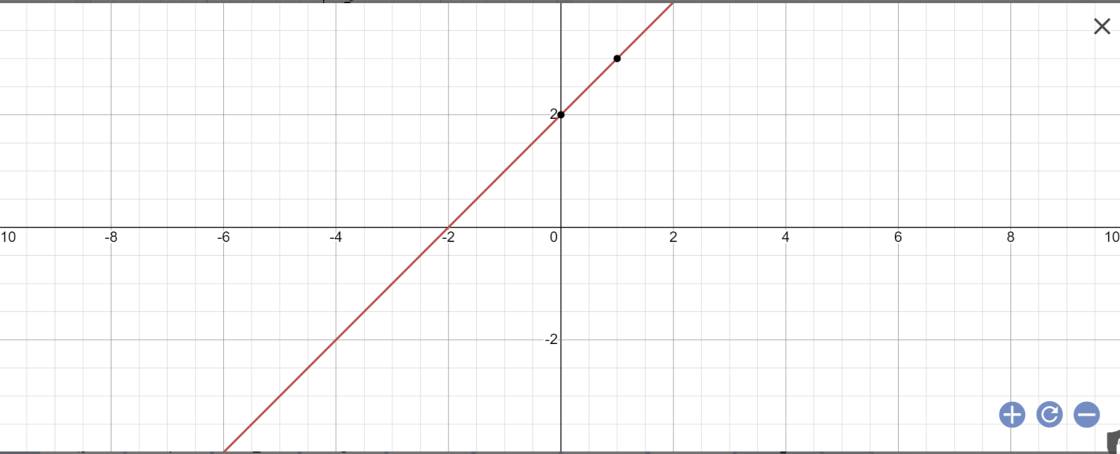
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
2: Thay x=1 và y=0 vào (d), ta được:
\(1\left(m-1\right)+m=0\)
=>2m-1=0
=>m=1/2
3:
y=(m-1)x+m
=mx-x+m
=m(x+1)-x
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x+1=0\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Câu 3 (2,0 điểm). Cho hàm số y = (m - 2) x + 2 với m khác 2 có đồ thị là đường thẳng (d)
b) Tìm m để đường thẳng (d) song song với đường thẳng (d1) : y = - 5x + 1
c) Đường thẳng (d) cắt trục Ox tại điểm A, cắt trục Oy tại điểm B. Tìm giá trị của m để diện tích tam giác ABO bằng 1
Em cần gấp ạ
b: Để (d)//(d1) thì m-2=-5 và 2<>1(đúng)
=>m=-3
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-2}\end{matrix}\right.\)
=>\(OA=\dfrac{2}{\left|m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)\cdot0+2=2\end{matrix}\right.\)
=>OB=2
\(S_{OAB}=1\)
=>\(\dfrac{1}{2}\cdot OA\cdot OB=1\)
=>\(\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-1\right|}=1\)
=>\(\left|m-1\right|=2\)
=>\(\left[{}\begin{matrix}m-1=2\\m-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Cho (O,R) đường kính AB. Trên tiếp tuyến Ax lấy AM= R x căn 3, dựng tiếp tuyến MN A. Xác định đường tròn qua 4 điểm: A,M,N,O B. Đường thẳng vuông góc với AB tại O cắt BN tại . Chứng minh OM//BE. C. Các tứ giác BEMO, AMEO, là hình gì D. Tính các góc và diện tích của tứ giác AMEB
a: Xét tứ giác MAON có \(\widehat{MAO}+\widehat{MNO}=90^0+90^0=180^0\)
nên MAON là tứ giác nội tiếp đường tròn đường kính MO
=>ĐƯờng tròn đi qua bốn điểm A,M,N,O là đường tròn đường kính MO
b: Xét (O) có
MA,MN là tiếp tuyến
Do đó: MA=MN
=>M nằm trên đường trung trực của AN(1)
OA=ON
=>O nằm trên đường trung trực của AN(2)
Từ (1) và (2) suy ra OM là đường trung trực của AN
=>OM\(\perp\)AN(3)
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
=>AN\(\perp\)NB
=>AN\(\perp\)BE(4)
Từ (3) và (4) suy ra OM//BE
c: Xét ΔMAO vuông tại A và ΔEOB vuông tại O có
OA=OB
\(\widehat{MOA}=\widehat{EBO}\)(hai góc đồng vị, MO//EB)
Do đó: ΔMAO=ΔEOB
=>MO=EB
Xét tứ giác BOME có
OM//BE
OM=BE
Do đó: BOME là hình bình hành
=>OB//EM và OB=ME
OB//ME
A\(\in\)OB
Do đó: OA//ME
OA=OB
OB=ME
Do đó: OA=ME
Xét tứ giác AOEM có
AO//EM
AO=EM
Do đó: AOEM là hình bình hành
Hình bình hành AOEM có \(\widehat{MAO}=90^0\)
nên AOEM là hình chữ nhật
d: ΔMAO vuông tại A
=>\(MA^2+OA^2=MO^2\)
=>\(MO^2=R^2+\left(R\sqrt{3}\right)^2=4R^2\)
=>MO=2R
=>EB=2R
Xét ΔEOB vuông tại O có \(cosB=\dfrac{BO}{EB}=\dfrac{1}{2}\)
nên góc B=60 độ
ME//AB
=>\(\widehat{MEB}+\widehat{B}=180^0\)
=>\(\widehat{MEB}=180^0-60^0=120^0\)
AOEM là hình chữ nhật
=>\(\widehat{EMA}=\widehat{MAO}=90^0\)
=>\(\widehat{EMA}=\widehat{MAB}=90^0\)
Diện tích tứ giác AEMB là:
\(S_{AEMB}=\dfrac{1}{2}\left(ME+AB\right)\cdot AM=\dfrac{1}{2}\cdot R\sqrt{3}\left(R+2R\right)=\dfrac{R\sqrt{3}}{2}\cdot3R=3\sqrt{3}\cdot\dfrac{R^2}{2}\)
Cho 2 hàm số bậc nhất y=4x-2 và y=-x + 3 A. Vẽ trên cùng 1 mặt phẳng tọa độ Oxy đồ thị hai hàm số y=4x -2 (d1) và y= -x +3 (d2) B. Gọi M là giao điểm của hai đường thẳng d1 và d2. Tìm tọa độ điểm M C. Tính góc tạo bởi 2 đường thẳng d1, d2 với trục Ox (làm tròn đến phút) D. Tìm đường thẳng d cắt d1 tại điềm A có tung độ là 6 và cắt d2 tại điểm B có hoành độ bằng nửa tung độ A. Tính chu vi và các góc tam giác AMB
a: 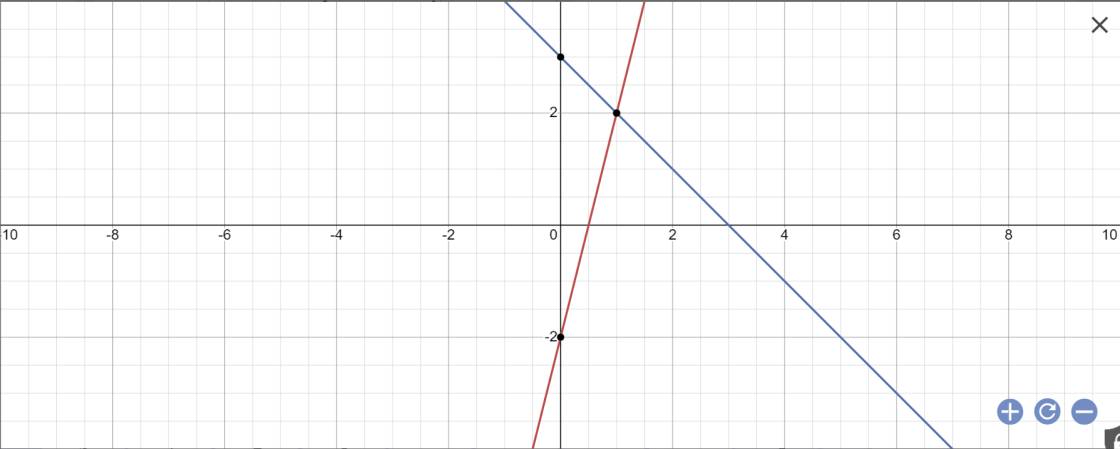
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)
2 ô tô khởi hành từ 2 địa điểm
A và B cách nhau 210 km đi ngược chiều sau 3 giờ gặp nhâu. tính vận tốc mỗi ô tô, biết vận tốc ô tô đi từ A lớn hơn vận tốc ô tô từ B 10km/h
Gọi vận tốc ô tô đi từ A là: x (km/h)
vận tốc ô tô đi từ B là: x-10 (km/h) (x>10)
Theo bài ra ta có:
\(x.3+\left(x-10\right).3=210\)
\(4x-30=210\)
\(x=60\)
=> vận tốc ô tô đi từ A là 60 km/h
vận tốc ô tô đi từ B là 50 km/h