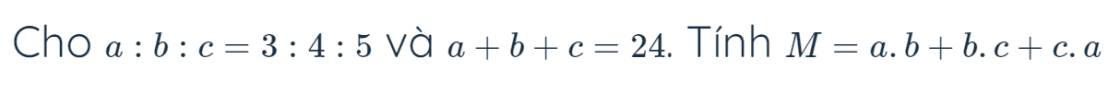Đại số lớp 7

Đề thiếu vế phải rồi em

a) Số tiền phải trả cho 1 lít xăng là:

$68450:3,7=18500$ (đồng)

Khi đổ đầy xăng loại đó, cô Hoa phải trả:

$18500\cdot4,5=83250$ (đồng)

b) Nếu phải trả $388500$ đồng, một xe ô tô sẽ được đổ số lít xăng là:

$388500:18500=21(l)$

P/s: Me too =))

\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{ab}{cd}\)

=>\(cd\left(a^2+b^2\right)=ab\left(c^2+d^2\right)\)

=>\(cda^2+cdb^2=abc^2+abd^2\)

=>\(cda^2-abc^2=abd^2-cdb^2\)

=>\(ac\left(da-bc\right)=bd\left(ad-cb\right)\)

=>\(\left(ac-bd\right)\left(ad-bc\right)=0\)

=>\(\left[{}\begin{matrix}ac=bd\\ad=bc\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}\dfrac{a}{b}=\dfrac{d}{c}\\\dfrac{a}{b}=\dfrac{c}{d}\end{matrix}\right.\)

x:2=y:(-5)

=>\(\dfrac{x}{2}=\dfrac{y}{-5}\)

mà x-y=-7

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=-\dfrac{7}{7}=-1\)

=>\(x=-1\cdot2=-2;y=\left(-1\right)\cdot\left(-5\right)=5\)

\(\dfrac{5-2x}{3}=\dfrac{4x-1}{-5}\)

\(\Leftrightarrow-5\left(5-2x\right)=3\left(4x-1\right)\)

\(\Leftrightarrow-25+10x=12x-3\)

\(\Leftrightarrow2x=-22\)

\(\Leftrightarrow x=-11\)

\(\dfrac{5-2x}{3}=\dfrac{4x-1}{-5}\)

=>\(3\left(4x-1\right)=-5\left(5-2x\right)\)

=>\(12x-3=-25+10x\)

=>2x=-22

=>\(x=-11\)

\(\dfrac{x}{3}=\dfrac{7}{5}\)

=>\(x=7\cdot\dfrac{3}{5}=\dfrac{21}{5}\)

\(x-y=2^2\)

=>\(x-y=4\)

=>\(y=\dfrac{21}{5}-4=\dfrac{1}{5}\)

\(x^4+x^3-2x^2+x+a⋮x+1\)

=>\(x^4+x^3-2x^2-2x+3x+3+a-3⋮x+1\)

=>a-3=0

=>a=3

\(\dfrac{x}{3}=\dfrac{y}{4}\)

=>\(\dfrac{x}{15}=\dfrac{y}{20}\)(1)

\(\dfrac{y}{5}=\dfrac{z}{6}\)

=>\(\dfrac{y}{20}=\dfrac{z}{24}\left(2\right)\)

Từ (1),(2) ta có \(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}\)

mà x+y=78

nên áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}=\dfrac{x+y}{15+20}=\dfrac{78}{35}\)

=>\(x=\dfrac{78}{35}\cdot15=\dfrac{234}{7};y=78\cdot\dfrac{20}{35}=\dfrac{312}{7};z=\dfrac{78}{35}\cdot24=\dfrac{1872}{35}\)

x/3 = y/4 ⇒ x/15 = y/20 (1)

y/5 = z/6 ⇒ y/20 = z/24 (2)

Từ (1) và (2) ⇒ x/15 = y/20 = z/24

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/15 = y/20 = z/24 = (x + y)/(15 + 20) = 78/35

x/15 = 78/35 ⇒ x = 78/35 . 15 = 234/7

y/20 = 78/35 ⇒ y = 78/35 . 20 = 312/7

z/24 = 78/35 ⇒ z = 78/35 . 24 = 1872/35

Vậy x = 234/7; y = 312/7; z = 1872/35

\(\dfrac{x}{2}=\dfrac{y}{3}\)

=>\(\dfrac{x}{4}=\dfrac{y}{6}\)

\(\dfrac{y}{2}=\dfrac{z}{5}\)

=>\(\dfrac{y}{6}=\dfrac{z}{15}\)

=>\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{15}\)

mà x+y+z=25

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{15}=\dfrac{x+y+z}{4+6+15}=\dfrac{25}{25}=1\)

=>x=4;y=6;z=15

\(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{4}=\dfrac{y}{6}\)

\(\dfrac{y}{2}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{15}\)

\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{15}=\dfrac{z+y+z}{4+6+15}=\dfrac{25}{25}=1\)

\(\Rightarrow\left\{{}\begin{matrix}x=4.1=4\\y=6.1=6\\z=15.1=15\end{matrix}\right.\)

Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{24}{12}=2\)

=>\(a=2\cdot3=6;b=2\cdot4=8;c=2\cdot5=10\)

\(a\cdot b+b\cdot c+c\cdot a\)

\(=6\cdot8+8\cdot10+6\cdot10\)

\(=48+80+60=128+60=188\)