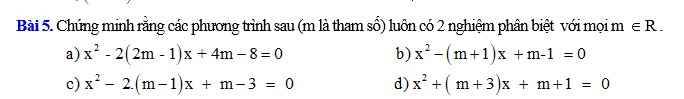a: \(x^2-2\left(2m-1\right)x+4m-8=0\)
\(\Delta=\left[-2\left(2m-1\right)\right]^2-4\cdot1\left(4m-8\right)\)
\(=4\left(4m^2-4m+1\right)-4\left(4m-8\right)\)
\(=16m^2-16m+4-16m+32\)
\(=16m^2-32m+36\)
\(=16m^2-32m+16+20=\left(4m-4\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b:
\(x^2-\left(m+1\right)x+m-1=0\)
\(\Delta=\left[-\left(m+1\right)\right]^2-4\cdot1\left(m-1\right)\)
\(=\left(m+1\right)^2-4\left(m-1\right)\)
\(=m^2+2m+1-4m+4=m^2-2m+5\)
\(=\left(m-1\right)^2+4>=4>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
c:\(x^2-2\left(m-1\right)x+m-3=0\)
\(\Delta=\left[-2\left(m-1\right)\right]^2-4\cdot1\left(m-3\right)\)
\(=4\left(m-1\right)^2-4\left(m-3\right)\)
\(=4m^2-8m+4-4m+12\)
\(=4m^2-12m+16=4m^2-12m+9+7\)
\(=\left(2m-3\right)^2+7>=7>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
d: \(x^2+\left(m+3\right)x+m+1=0\)
\(\Delta=\left(m+3\right)^2-4\cdot1\left(m+1\right)\)
\(=m^2+6m+9-4m-4\)
\(=m^2-2m+5=\left(m-1\right)^2+4>=4>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt