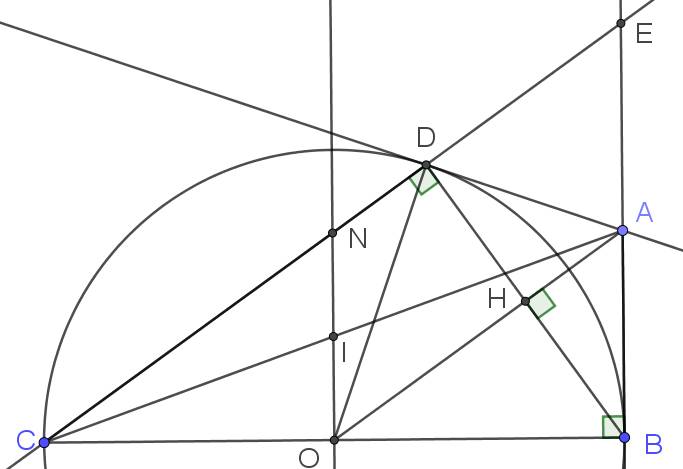
a) Trong tam giác $BCD$ có $OC=OB=OD (=R)$, do đó tam giác BCD vuông tại D.
b) Áp dụng tính chất hai tiếp tuyến $AD$ và $AB$ cắt nhau tại $A$, ta có $AB=AD$.
Mặt khác $OB=OD$, do đó $OA$ là đường trung trực của $BD$, từ đây suy ra $OA$ vuông góc với $BD$.
Áp dụng hệ thức lượng trong tam giác vuông $ODA $ vuông tại $D$:
$R^2 = OD^2 = OH . OA$
c) $CD$ cắt $AB$ tại $E$.
Tam giác $ABD$ cân tại $A$(chứng minh trên), suy ra $\widehat{ADB}$ $=$ $\widehat{ABD}$.
Mặt khác, ta có
$\widehat{DEA} + \widehat{DBA}=90^{o}$, do đó $\widehat{DEA} + \widehat{ADB}=90^{o}$.
mà $\widehat{EDA} + \widehat{ADB}=90^{o}$.
Suy ra $\widehat{DEA}=\widehat{EDA}$, suy ra tam giác DEA cân tại A, suy ta $AD=AE=AB$. (*)
Áp dụng định lí Ta-let cho tam giác $CAE$ và tam giác $CBA$.
\(\dfrac{OI}{AB}=\dfrac{IN}{EA}\left(=\dfrac{CI}{CA}\right)\)
Từ đây, do (*), nên ta có $OI=IN$, ta suy ra điều cần chứng minh.