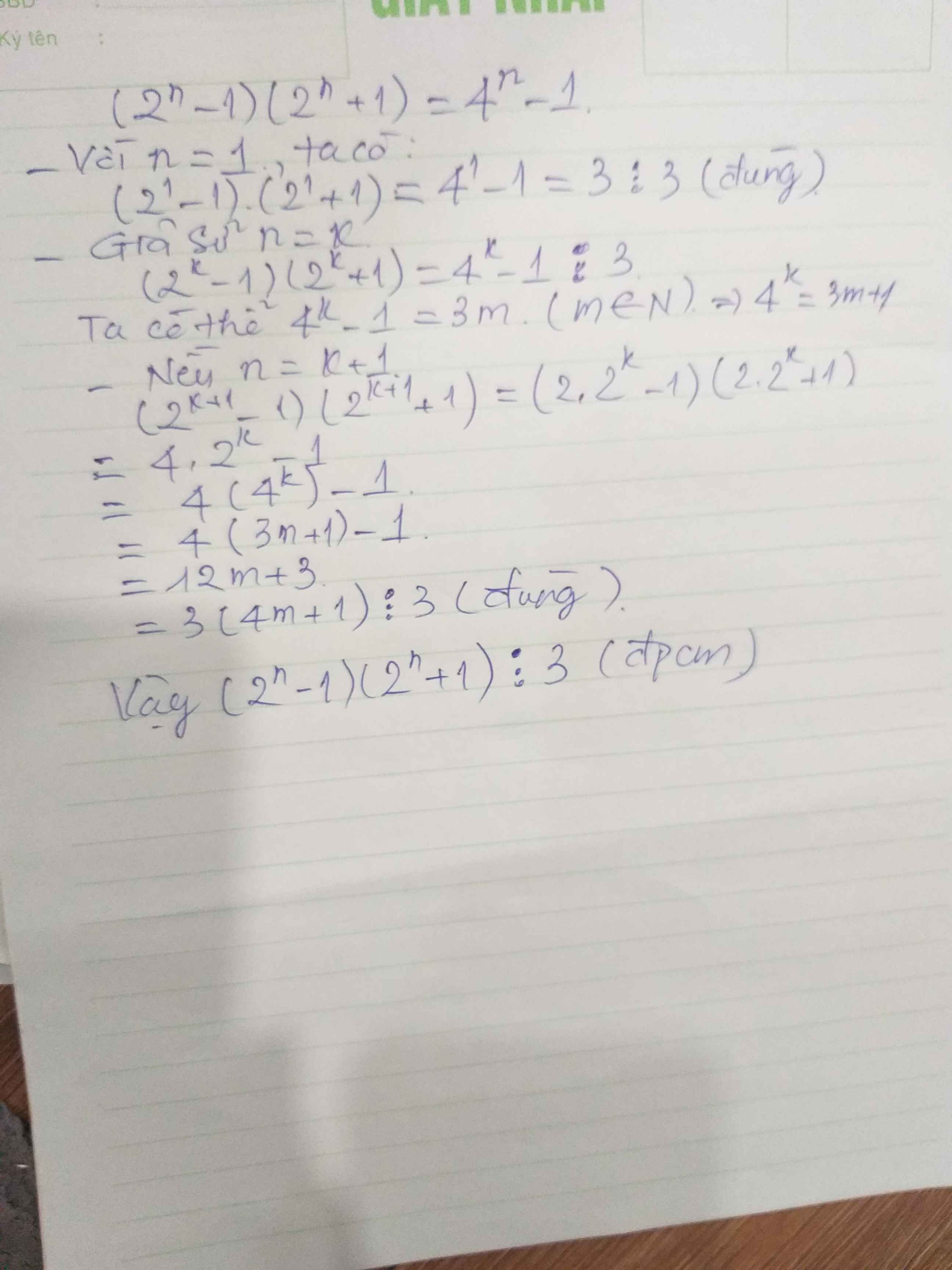Chứng minh ( 2^n - 1) x ( 2^n +1) chia hết cho 3
Bài 8. Quan hệ chia hết và tính chất
Ta có: Với `n` là số tự nhiên thì:
`2^n` có dạng `3k+1` hoặc `3k + 2` vì `2^n` không chia hết `3 (k in N)`
Xét `2^n = 3k + 1 `
`=> 2^n - 1 = 3k` chia hết cho 3
`=> 3k . (2^n + 1)` chia hết cho 3
Hay `(2^n -1)(2^n+1)` chia hết cho 3
Xét `2^n = 3k + 2 `
`=> 2^n +1 = 3k + 3` chia hết cho 3
`=> (3k + 3) . (2^n + 1) ` chia hết cho 3
Hay `(2^n -1)(2^n+1)` chia hết cho 3
Vậy ...
Đúng 1
Bình luận (0)
99^20 + 9, hãy chứng tỏ nó chia hết cho 5 và 9
\(99^{20}+9=9^{20}\cdot11^{20}+9=9\left(9^{19}\cdot11^{20}+1\right)⋮9\)
\(99^{20}\) có chữ số tận cùng trùng với chữ số tận cùng của 920
mà 920 có chữ số tận cùng là 1
nên 9920 có chữ số tận cùng là 1
=>\(99^{20}+9\) có chữ số tận cùng là chữ số tận cùng của 1+9=10
=>9920+9 có chữ số tận cùng là 0
=>\(99^{20}+9⋮5\)
Đúng 2
Bình luận (0)