Bài 10. Số nguyên tố

1. SỐ NGUYÊN TỐ VÀ HỢP SỐ

• Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
• Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.

Chú ý: Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.

Ví dụ. Trong các số sau, số nào là số nguyên tố, số nào là hợp số? Vì sao?

a) 225;

b) 37;

c) 2 430.

Giải:

a) Số 225 có tận cùng là 5 nên nó chia hết cho 5. Do đó, ngoài hai ước là 1 và 225 nó còn có thêm ước là 5. Vậy, 225 là hợp số.

b) Số 37 chỉ có hai ước là 1 và 37 nên nó là số nguyên tố.

c) Số 2 430 có 2 + 4 + 3 + 0 = 9 chia hết cho 9, suy ra 2 430 chia hết cho 9. Do đó, ngoài hai ước là 1 và 2 430 nó còn có thêm ước là 9. Vậy, 2 430 là hợp số.

Chú ý: Để khẳng định một số là hợp số, ta thường sử dụng các dấu hiệu chia hết để tìm ra một ước khác 1 và chính nó.

Chú ý: Để biết một số tự nhiên nhỏ hơn 1000 có là số nguyên tố hay không, ta có thể tra bảng số nguyên tố dưới đây:

2. PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ

Với 18 = 2.9. Ta nói 2 là một ước nguyên tố của 2 hay 2 là một thừa số nguyên tố của tích 2.9.

a) Phân tích một số tự nhiên ra thừa số nguyên tố

• Mọi hợp số đều có thể phân tích được thành tích của các thừa số nguyên tố. 

Chẳng hạn, ta phân tích số 36 như sau:

Ta nói rằng ta đã phân tích số 36 ra thừa số nguyên tố, được kết quả

36 = 2.2.3.3 và được viết gọn là 36 = 2².3².

• Người ta quy ước dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính nó.
• Khi phân tích một số ra thừa số nguyên tố, trong kết quả ta thường viết các thừa số theo thứ tự từ bé đến lớn và viết tích các thừa số giống nhau dưới dạng lũy thừa.

Ví dụ 1. Phân tích các số 45 và 72 ra thừa số nguyên tố.

Giải:

• 45 = 5.9 = 5.3.3 = 3².5.

Vậy, phân tích số 45 ra thừa số nguyên tố, ta được 45 = 3².5.

• 72 = 8.9 = 2.2.2.3.3 = 2³.3².

Vậy, phân tích số 72 ra thừa số nguyên tố, ta được 72 = 2³.3².

b) Phương pháp phân tích theo sơ đồ cây

Quá trình phân tích số 36 ra thừa số nguyên tố như trên có thể được trình bày dưới dạng một sơ đồ gọi là sơ đồ cây.

Ta cũng có thể phân tích số 36 ra thừa số nguyên tố theo một sơ đồ cây khác như sau:

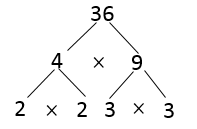
Vậy, 36 = 2.2.3.3 = 2².3².

Ví dụ 2. Phân tích 60 ra thừa số nguyên tố theo sơ đồ cây.

Vậy, 60 = 2.2.3.5 = 2².3.5.

c) Phương pháp phân tích theo sơ đồ cột

Ta có thể phân tích một số ra thừa số nguyên tố theo sơ đồ cột. 

Chẳng hạn, ta phân tích số 36 thành tích các thừa số nguyên tố theo cách làm như sau:

Vậy, 36 = 2².3².

Sơ đồ phân tích số 36 thành tích các thừa số nguyên tố như trên gọi là sơ đồ cột.

Ví dụ 3. Phân tích số 75 ra thừa số nguyên tố theo sơ đồ cột.

Giải:

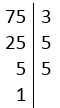
Vậy 75 = 3.5.5 = 3.5².