Bài 8: Các trường hợp đồng dạng của tam giác vuông

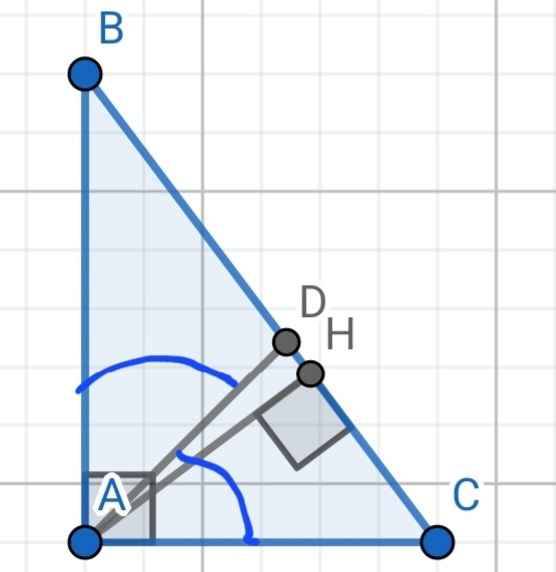
a) Do AD là phân giác của ∠A

⇒ DB/DC = 8/6 = 4/3

b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:

∠HAB = ∠HCA (cùng phụ ∠B)

⇒ ∆AHB ∽ ∆CHA (g-g)

⇒ AH/CH = AB/CA

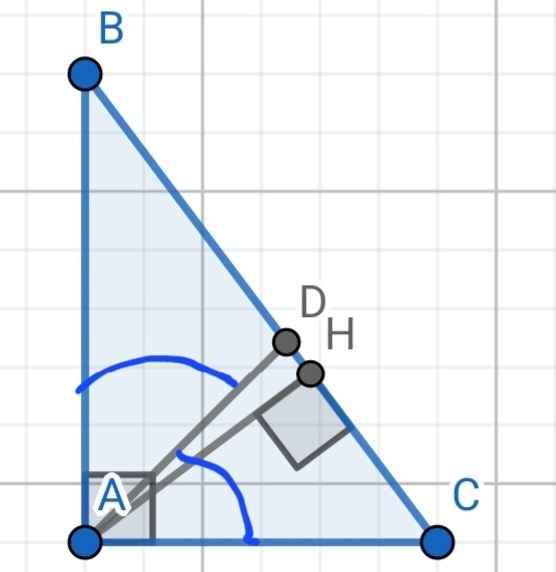
a) Do AD là phân giác của ∠A

⇒ DB/DC = 8/6 = 4/3

b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:

∠HAB = ∠HCA (cùng phụ ∠B)

⇒ ∆AHB ∽ ∆CHA (g-g)

⇒ AH/CH = AB/CA

a: DB/DC=AB/AC=4/3

b: Sửa đề: AH/CA=AB/BC

\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)

=>AH*BC=AB*AC

=>AH/AC=AB/CB

Diện tích đáy:

\(S=\dfrac{8.6}{2}=24\left(cm^2\right)\)

Thể tích hình lăng trụ:

\(V=S.h=24.10=240\left(cm^3\right)\)

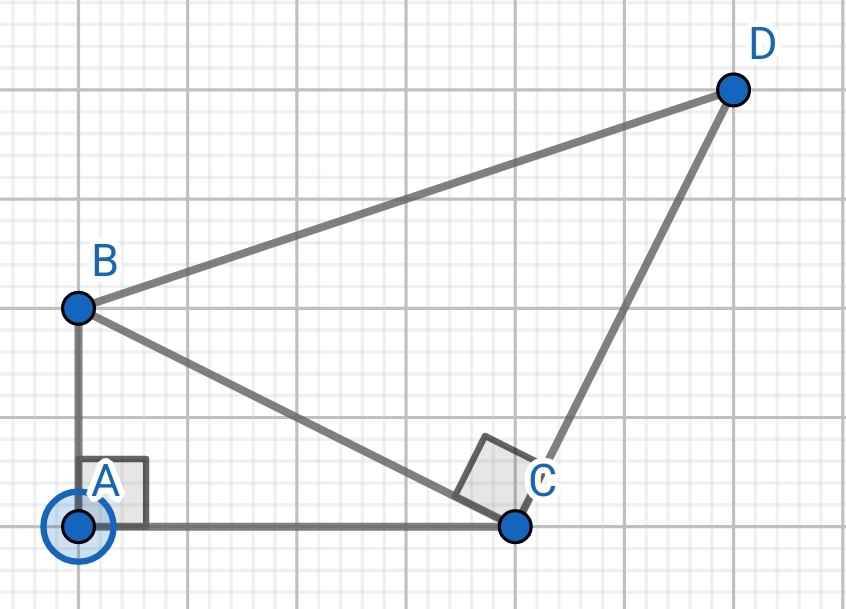
∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

⇒ AB² = BC² - AC²

= 12² - 8²

= 80

⇒ AB = \(4\sqrt{5}\) (cm)

∆CDB vuông tại C

⇒ BD² = CD² + BC² (Pytago)

⇒ CD² = BD² - BC²

= 18² - 12²

= 180

⇒ CD = \(6\sqrt{5}\) (cm)

Xét ∆ABC và ∆CDB có:

\(\dfrac{BC}{BD}=\dfrac{12}{18}=\dfrac{2}{3}\)

\(\dfrac{AB}{CD}=\dfrac{4\sqrt{5}}{6\sqrt{5}}=\dfrac{2}{3}\) 

\(\dfrac{AC}{BC}=\dfrac{8}{12}=\dfrac{2}{3}\)

⇒ \(\dfrac{BC}{BD}=\dfrac{AB}{CD}=\dfrac{AC}{BC}=\dfrac{2}{3}\) 

Vậy ∆ABC ∽ ∆CDB (c-c-c)

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

góc B chung

=>ΔABH đồng dạng với ΔCBA

b: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

AH=9*12/15=7,2cm

c: AD là phân giác

=>AD/DC=BA/BC=AH/AC

=>AD*AC=AH*DC

điểm Z đâu vậy bạn

ΔAEB vuông tại E có góc A=45 độ

nên ΔEAB vuông cân tại E

=>\(\dfrac{AE}{AB}=\dfrac{1}{\sqrt{2}}\)

góc BFC=góc BEC=90 độ

=>BFEC nội tiếp

=>góc AFE=góc ACB

=>ΔAFE đồng dạng với ΔACB

=>\(\dfrac{S_{AFE}}{S_{ACB}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)

=>\(S_{AFE}=50\)

=>\(S_{BFEC}=50\)

a: Xet ΔABC vuông tại A và ΔHBA vuôngtại H có

góc B chung

=>ΔABC đồng dạngvới ΔHBA

b: Xet ΔCHM vuông tại H và ΔCKB vuông tại K có

góc HCM chung

=>ΔCHM đồng dạngvới ΔCKB

=>CH/CK=CM/CB

=>CH*CB=CK*CM

c: Xét ΔBHD vuông tại H và ΔBKC vuông tại K có

goc HBD chung

=>ΔBHD đồng dạng với ΔBKC

=>BH/BK=BD/BC

=>BH/BD=BK/BC

=>ΔBHK đồng dạng vơi ΔBDC
=>góc BKH=góc BCD

xét ΔABC vuông tại A, áp dụng tính chất pytago ta có 

\(BC^2=AC^2+AB^2\) 

         \(=6^2+5^2\) 

          \(=25+36\)

          \(=56\)

=>\(BC=\sqrt{61}\approx7,8\left(cm\right)\)

a: Xét ΔAHB vuông tạiH và ΔCAB vuông tại A có

góc B chung

=>ΔAHB đồng dạng với ΔCAB

b: góc ADH=góc AEH=góc DAE=90 độ

=>ADHE là hình chữ nhật

c:

\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

 \(AH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\)

=>DE=7,2cm