Tiếp tuyến của đồ thì hàm số y=\(\dfrac{x-3}{x+1}\) (c) cùng với hai đường tiệm cận tạo thành một tam giác có diện tích bằng?
Bài 5b: Tiếp tuyến của đồ thị hàm số
Lời giải:
Ta có: \(\lim_{x\to \infty} \frac{x-3}{x+1}=\lim_{x\to \infty}\frac{1-\frac{3}{x}}{1+\frac{1}{x}}=\frac{1}{1}\)
Do đó tiệm cận ngang : \(y=1\)
\(\lim _{x\to -1}\frac{x-3}{x+1}=\lim_{x\to -1}(1-\frac{4}{x+1})=1-\lim _{x\to -1}\frac{4}{x+1}=\infty\)
Do đó tiệm cận đứng \(x=-1\)
Gọi $I$ là giao điểm của hai tiệm cận thì \(I(-1;1)\)
Ta có: \(y'=\frac{4}{(x+1)^2}\) nên pt tiếp tuyến tại điểm $x_0$ là:
\(d:y=\frac{4}{(x_0+1)^2}(x-x_0)+\frac{x_0-3}{x_0+1}\)
Giao điểm \(d\cap \text{TCĐ}\) là: \(A=\left(-1; \frac{x_0-7}{x_0+1}\right)\)
Giao điểm \(d\cap \text{TCN}\) là: \(B=(2x_0+1,1)\)
Do đó: \(IA=|\frac{x_0-7}{x_0+1}-1|=|\frac{-8}{x_0+1}|\)
\(IB=|2x_0+1-(-1)|=2|x_0+1|\)
Do đó diện tích tam giác hợp bởi ba đường là:
\(S_{IAB}=\frac{IA.IB}{2}=\frac{|\frac{-8}{x_0+1}|.2|x_0+1|}{2}=8\) (đơn vị diện tích)
Đúng 0
Bình luận (1)
Tiếp tuyến của parabol y= 4-x2 tại điểm (1;3) tạo với hai trục toạ độ một tam giác vuông. Diện tích tam giác vuông đó là ?
mọi người giúp mình với,mình cảm ơn ạ
Lời giải:
Ta có: \(y'=-2x\) nên phương trình tiếp tuyến tại điểm \((1;3)\) là:
\(y=-2(x-1)+3\Leftrightarrow y=-2x+5\) \((d)\)
Khi đó, \(\left\{\begin{matrix} (d)\cap Ox=\left(\frac{5}{2},0\right)\\ (d)\cap Oy=(0,5)\end{matrix}\right.\)
Suy ra độ dài hai cạnh góc vuông là: \(\frac{5}{2}\) và $5$
Do đó, diện tích tam giác vuông là:
\(S=\frac{1}{2}.\frac{5}{2}.5=\frac{25}{4}\) (đơn vị diện tích)
Đúng 0
Bình luận (0)
Cho hàm số : yfrac{4}{3}x^3-left(2m+1right)x^2+left(m+2right)x+frac{1}{3}, có đồ thị left(C_mright), m là tham số. Gọi A là giao điểm của left(C_mright) với trục tung. Tìm m sao cho tiếp tuyến của left(C_mright) tại A tạo với 2 trục tọa độ một tam giác có diện tích bằng frac{1}{3}
Đọc tiếp
Cho hàm số : \(y=\frac{4}{3}x^3-\left(2m+1\right)x^2+\left(m+2\right)x+\frac{1}{3}\), có đồ thị \(\left(C_m\right)\), m là tham số. Gọi A là giao điểm của \(\left(C_m\right)\) với trục tung. Tìm m sao cho tiếp tuyến của \(\left(C_m\right)\) tại A tạo với 2 trục tọa độ một tam giác có diện tích bằng \(\frac{1}{3}\)
Ta có : \(A\left(0;\frac{1}{3}\right)\) và \(y'=4x^2-2\left(2m+1\right)x+m+2\)
Suy ra \(y'\left(0\right)=m+2\)
Tiếp tuyến của d cắt Ox tại \(B\left(-\frac{1}{3m+6};0\right)\) (m=-2 không thỏa mãn yêu cầu bài toán)
Khi đó diện tích của tam giác tạo bởi d với 2 trục tọa độ là :
\(S=\frac{1}{2}OA.OB=\frac{1}{2}.\frac{1}{3}.\left|\frac{-1}{3m+6}\right|=\frac{1}{18\left|m+2\right|}\)
Theo giả thiết ta có : \(\frac{1}{18\left|m+2\right|}=\frac{1}{3}\Leftrightarrow\left|m+2\right|=\frac{1}{6}\)
\(\Leftrightarrow m=-\frac{13}{6}\) hoặc \(m=-\frac{11}{6}\)
Đúng 0
Bình luận (0)
Tìm các tiệm cận đứng và ngang của đồ thị hàm số \(y=\dfrac{3x-2}{2x-3}\)
Có\(x\rightarrow\mp\infty\) lim \(\dfrac{3x-2}{2x-3}=\dfrac{3}{2}\Rightarrow y=\dfrac{3}{2}\) là đường tiệm cận ngang của đồ thị hàm số
\(x\rightarrow\dfrac{3^-}{2}\)lim \(\dfrac{3x-2}{2x-3}=+\infty\Rightarrow x=\dfrac{3}{2}\) là tiệm cận đứng của đồ thị hàm số
Đúng 0
Bình luận (2)
Lời giải:
Ta có: \(\lim_{x\mapsto +\infty}\frac{3x-2}{2x-3}=\frac{3}{2}=\lim_{x\mapsto +\infty}\frac{3-\frac{2}{x}}{2-\frac{3}{x}}=\frac{3}{2}\)
\(\Rightarrow y=\frac{3}{2}\)là tiệm cận ngang
Có: \(\lim _{x\mapsto \frac{3}{2}^+}y=\lim_{x\mapsto \frac{3}{2}^+}\frac{3x-2}{2x-3}=+\infty\) nên \(x=\frac{3}{2}\) là tiệm cận đứng
Đúng 0
Bình luận (1)
\(y=\dfrac{3x-2}{2x-3}=\dfrac{3}{2}+\dfrac{5}{4x-6}\)
tịm cận đứng x =3/2
tiệm cận ngang x =6/4=2/3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng họ đường thẳng sau luôn tiếp xúc với một đường cong cố định \(\left(C_m\right):y=2mx^3-x^2+\left(2m+1\right)x-m^2+2\)
Giả sử \(M\left(x_0;y_0\right)\) là điểm mà họ \(\Delta_{\alpha}\) không đi qua. Khi đó phương trình sau vô nghiệm với mọi m : \(m^2-2\left(x^3_0+x_0\right)m+y_0+x^2_0-x_0-2=0\)
\(\Leftrightarrow\Delta'=\left(x^3_0+x_0\right)^2-\left(y_0+x^2_0-x_0-2\right)< 0\)
\(\Leftrightarrow y_0>x^6_0+2x^4_0+x_0+2\)
Xét phương trình : \(2mx^3-x^2+\left(2m+1\right)x-m^2+2=x^6+2x^4+x+2\)
\(\Leftrightarrow m^2-2\left(x^3+x\right)m+\left(x^3+x\right)^2=0\)
\(\Leftrightarrow\left(x^3+x-m\right)^2=0\) (*)
Vì phương trình \(x^3+x-m=0\) luôn có nghiệm nên (*) luôn có nghiệm bội.
Vậy \(\left(C_m\right)\) luôn tiếp xúc với đường cong \(y=x^6+2x^4+x+2\)
Đúng 0
Bình luận (0)
CÁch 1: G/s họ đường thằng trên luôn tiếp xúc với parabol cố định: )
Khi đó: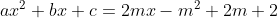 có nghiệm kép với mọi m
có nghiệm kép với mọi m
hay+c+m^2-2m-2=0) có nghiệm kép với mọi m
có nghiệm kép với mọi m
Cách 2: Gọi) là các điểm mà họ đường thẳng trên không đi qua.
là các điểm mà họ đường thẳng trên không đi qua.
Hay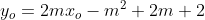 vô nghiệm ẩn m
vô nghiệm ẩn m
+y_o-2=0) vô nghiệm ẩn m
vô nghiệm ẩn m
^2-(y_o-2)%3C0&space;\\\Leftrightarrow&space;x_o^2+2x_o+3%3Cy_o)
Xét đường biên:y=x^2+2x+3)
Lập phương trình hoành độ giao điểm ta được:^2=0)
Phương trình này luôn có 1 nghiệm kép nên (dm) luôn tiếp xúc (P)
Khi đó:
hay
Cách 2: Gọi
Hay
Xét đường biên:
Lập phương trình hoành độ giao điểm ta được:
Phương trình này luôn có 1 nghiệm kép nên (dm) luôn tiếp xúc (P)
Đúng 0
Bình luận (0)
Tìm điểm trên đồ thị hàm số y=\(-2x^3\)+\(6x^{^2}\)+x-2 sao cho hệ số góc của tiếp tuyến tại điểm đó đạt GTLN
A.(-1;3)
B.(1;-3)
C.(-1;-3)
D.(1;3)
viết phương trinh tiếp tuyến của đồ thị y=\(\dfrac{3x-2}{x-2}\) tạo với 2 trục tọa độ một tam giác cân là
Lời giải:
Ta có \(y=\frac{3x-2}{x-2}\Rightarrow y'=\frac{-4}{(x-2)^2}\)
Gọi \(a\) là hoành độ tiếp điểm của đường thẳng tiếp tuyến cần tìm.
PTTT: \(y=\frac{-4}{(a-2)^2}(x-a)+\frac{3a-2}{a-2}\)
\(\Leftrightarrow y=\frac{-4x}{(a-2)^2}+\frac{3a^2-4a+4}{(a-2)^2}\) \((d)\)
Ta có:
\(d\cap Ox =\left (\frac{3a^2-4a+4}{4},0\right)\)
\(d\cap Oy=\left(0,\frac{3a^2-4a+4}{(a-2)^2}\right)\)
Để PTTT tạo với hai trục tọa độ một tam giác cân thì :
\(\left |\frac{3a^2-4a+4}{4}\right|=\left |\frac{3a^2-4a+4}{(a-2)^2}\right|\)
\(\leftrightarrow\left[{}\begin{matrix}3a^2-4a+4=0\\\left(a-2\right)^2=4\end{matrix}\right.\)
Từ đây ta thu được $a=4$ hoặc $a=0$
Do đó PTTT là: \(\left[{}\begin{matrix}y=-x+9\\y=-x+1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1. Tìm điểm M thuộc (C) : y dfrac{x+1}{x-1}sao cho tiếp tuyến của (C) tại M vuông góc với IM, I là tâm đối xứng
2. Tìm những điểm trên đt y -2 mà từ đó có thể kẻ đc 3 tiếp tuyến tới (C): y -x^3+3x^2-2
3. Tìm những điểm trên đt y 2 mà từ đó có thể kẻ đc tới (C): y x^3-3x^{^{ }2}+2
a, đúng 2 tiếp tuyến
b, 3 tiếp tuyễn đến (C) trong đó có 2 tiếp tuyên vuông góc
4. Tìm M thuộc đồ thị y dfrac{2x-3}{x-2}sao cho tiếp tuyến của M tại (C) cắt 2 tiệm cận tại A,B sao cho AB nhỏ nhất.
Đọc tiếp
1. Tìm điểm M thuộc (C) : y =\(\dfrac{x+1}{x-1}\)sao cho tiếp tuyến của (C) tại M vuông góc với IM, I là tâm đối xứng
2. Tìm những điểm trên đt y = -2 mà từ đó có thể kẻ đc 3 tiếp tuyến tới (C): y = \(-x^3+3x^2-2\)
3. Tìm những điểm trên đt y = 2 mà từ đó có thể kẻ đc tới (C): y = \(x^3-3x^{^{ }2}+2\)
a, đúng 2 tiếp tuyến
b, 3 tiếp tuyễn đến (C) trong đó có 2 tiếp tuyên vuông góc
4. Tìm M thuộc đồ thị y = \(\dfrac{2x-3}{x-2}\)sao cho tiếp tuyến của M tại (C) cắt 2 tiệm cận tại A,B sao cho AB nhỏ nhất.
Đợi khi nào mk học đã nha!!Mk hứa mk sẽ giải bài này!!![]()
Đúng 0
Bình luận (0)
Cho hàm số y=(3x+6)/(x-1) (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến song song với đường thẳng d: 3x+4y-21
Lời giải:
Ta có \(y=\frac{3x+6}{x-1}\Rightarrow y'=\frac{-9}{(x-1)^2}\)
Gọi tiếp điểm của tiếp tuyến với đồ thị C là \(M\left(x_0,\frac{3x_0+6}{x_0-1}\right)\)
PTTT: \(y=f'(x_0)(x-x_0)+f(x_0)\)
\(\Leftrightarrow y=\frac{-9}{(x_0-1)^2}(x-x_0)+\frac{3x_0+6}{x_0-1}=\frac{-9x}{(x_0-1)^2}+\frac{3x_0^2+12x_0-6}{(x_0-1)^2}\)
Để ĐT trên song song với \(d:3x+4y-21=0\) thì:
\(\frac{-9}{(x_0-1)^2}=\frac{-3}{4}\Leftrightarrow x_0=1\pm 2\sqrt{3}\)
Do đó PTTT là: \(y=\frac{-3x}{4}+\frac{15\pm 12\sqrt{3}}{4}\Leftrightarrow 3x+4y-(15\pm 12\sqrt{3})=0\)
Đúng 0
Bình luận (0)
y = \(\dfrac{x+2}{2x+3}\)
Viết phương trình tiếp tuyến biết tiếp tuyến cắt Ox, Oy = A, B mà ∆AOB vuông cân ở O ?Lời giải:
Gọi hoành độ tiếp điểm là \(m\). PT tiếp tuyến là:
\(y=y'(m)(x-m)+y(m)=\frac{-1}{(2m+3)^2}(x-m)+\frac{m+2}{2m+3}\)
\(\Leftrightarrow y=\frac{2m^2+8m+6-x}{(2m+3)^2}(d)\)
$A,B$ lần lượt thuộc $Ox,Oy$ nên có tọa độ là \((a,0);(0,b)\)
Mặt khác \(A,B\in (d)\Rightarrow \)\(\left\{\begin{matrix} 0=\frac{2m^2+8m+6-a}{(2m+3)^2}\rightarrow a=2m^2+8m+6\\ b=\frac{2m^2+8m+6}{(2m+3)^2}\end{matrix}\right.\)
Tam giác $AOB$ vuông cân tại $O$. Vì hiển nhiên tam giác trên vuông nên chỉ xét tính chất cân. Từ đây ta có \(OA^2=OB^2\Leftrightarrow a^2=b^2\)
\(\Leftrightarrow \frac{(2m^2+8m+6)^2}{(2m+3)^4}=(2m^2+8m+6)^2\)\(\Rightarrow\left[{}\begin{matrix}m=-3\\m=-2\\m=-1\end{matrix}\right.\)
Suy ra PTTT có thể là: \(\left[{}\begin{matrix}y=\dfrac{-x}{9}\\y=-\left(x+2\right)\\y=-x\end{matrix}\right.\)
Vì $A,B$ không thể trùng $O$ nên PTTT là \(y=-(x+2)\)
Đúng 0
Bình luận (0)

