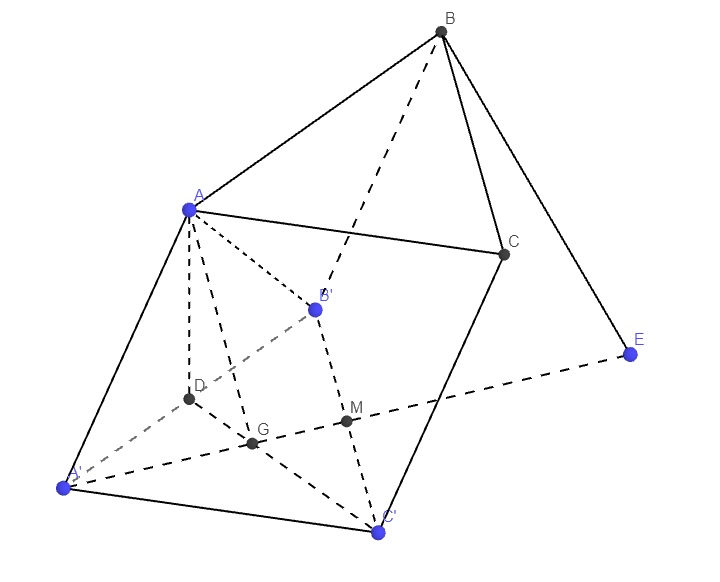
G là trọng tâm \(A'B'C'\Rightarrow\overrightarrow{A'G}=\dfrac{1}{3}\left(\overrightarrow{A'B'}+\overrightarrow{A'C'}\right)\)
\(\Rightarrow\overrightarrow{A'E}=3\overrightarrow{A'G}=\overrightarrow{A'B'}+\overrightarrow{A'C'}\)
\(\Rightarrow A'B'EC'\) là hình bình hành
\(\Rightarrow EC'\) song song và bằng A'B' nên EC' cũng song song và bằng AB
\(\Rightarrow ABEC'\) là hình bình hành
\(\Rightarrow BE||AC'\Rightarrow BE||\left(AGC'\right)\)
\(\Rightarrow d\left(AG;BE\right)=d\left(BE;\left(AGC'\right)\right)=d\left(B;\left(AGC'\right)\right)\)
Gọi D là trung điểm A'B' \(\Rightarrow C'D\perp A'B'\) (do tam giác ABC cân tại C nên A'B'C' cũng cân tại C') (1)
\(AA'=AB'\Rightarrow\Delta AA'B'\) cân tại A \(\Rightarrow AD\perp A'B'\) (2)
(1);(2)\(\Rightarrow A'B'\perp\left(AGC'\right)\)
Hay \(AB\perp\left(AGC'\right)\)
\(\Rightarrow\)\(d\left(B;\left(AGC'\right)\right)=AB=2a\)