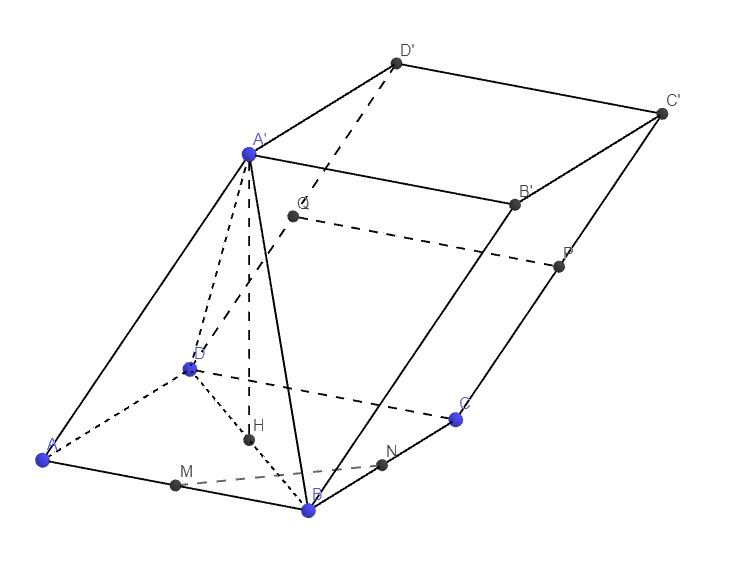
\(\left\{{}\begin{matrix}PQ||\left(ABCD\right)\\MN\in\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow d\left(PQ;MN\right)=d\left(PQ;\left(ABCD\right)\right)=d\left(Q;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(\left(ABCD\right);\left(A'B'C'D'\right)\right)\)
Ta có: \(A'D=A'B=A'A=a\) (các tam giác DAA' và A'AB đều) (1)
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
\(\Rightarrow AH=BH=DH\) (theo (1))
\(\Rightarrow H\) là tâm đường tròn ngoại tiếp ABD
\(\Rightarrow H\) là trung điểm BD (do tam giác ABD vuông tại A theo giả thiết)
\(\Rightarrow DH=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow A'H=\sqrt{A'D^2-DH^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow d\left(MN;PQ\right)=\dfrac{1}{2}A'H=\dfrac{a\sqrt{2}}{4}\)