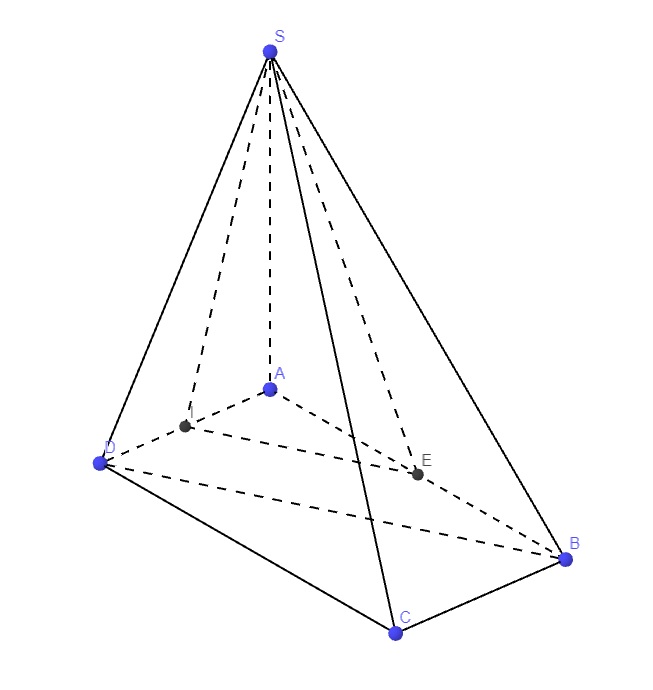
Cho hình chóp tam giác đều SABC có cạnh đáy bằng 2a và chiều cao bằng a√3. Gọi P là trung điểm của SA. Khoảng cách từ điểm P đến mặt phẳng (SBC) bằng Mọi người giúp mk với ạ. Mk cảm ơn
Bài 5: Khoảng cách
Cho hình chóp SABCD đáy là hình vuông cạnh A, SA vuông góc với (ABCD), SA=a căn 3 a, Cm BC vuông góc với (SAB) b, Tính (SB, (ABCD)) Giúp em vơia ạ em cầm gấp
a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: (SB;(ABCD))=(BS;BA)=góc SBA
\(\sin SBA=\dfrac{SA}{SB}=\dfrac{a\sqrt{3}}{2a}=\dfrac{\sqrt{3}}{2}\)
=>góc SBA=60 độ
Đúng 1
Bình luận (0)
Cho hình chóp sabcd có đáy là hình vuông cạnh a, mặt bên (SAB) đều và vuông góc với mặt phẳng đáy. gọi M là điểm trên sd sao cho SD=4SM
a. Tính khoảng cách từ trung điểm AB đến (SBC)
b. Tính khoảng cách từ điểm M đến (SBC)
Cho hình chóp S.ABCD, ABCD là hình thoi cạnh \(a\sqrt{3}\), SA= a, SB=SC=SA = \(a\sqrt{3}\). M là trung điểm của CD. Tính \(d\left(DM,BC\right)\)
Cho hình hộp ABCD.A'B'C'D' có đáy là hình vuông cạnh a. A' cách đều A,B,D của đáy và AA'=2a. Tính d(B, D'AC)
Mn giúp mình với ạ. Mình đang cần gấp 😥
Hướng dẫn: gọi O là tâm đáy thì \(A'O\perp\left(ABCD\right)\) \(\Rightarrow\) chóp \(A'.ABCD\) là chóp tứ giác đều
\(d\left(B;\left(D'AC\right)\right)=d\left(D;\left(D'AC\right)\right)\)
Gọi E là giao điểm A'D và AD' \(\Rightarrow E\) là trung điểm A'D
\(AC\perp\left(A'DB\right)\Rightarrow\left(A'DB\right)\perp\left(D'AC\right)\)
Mà \(OE=\left(A'DB\right)\cap\left(D'AC\right)\) nên từ D kẻ \(DF\perp OE\) thì \(DF\perp\left(D'AC\right)\)
Hay DF là đoạn cần tìm
Đúng 1
Bình luận (4)
giúp mik câu 1,2 với ạ mình dag cần gấp

1.
a. Do \(AD||BC\Rightarrow\left(SD;BC\right)=\left(SD;AD\right)=\widehat{SDA}\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là trung điểm AB \(\Rightarrow IE\) là đường trung bình tam giác ABD
\(\Rightarrow IE||BD\Rightarrow\left(SI;BD\right)=\left(SI;IE\right)=\widehat{SIE}\)
\(IE=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(SI=\sqrt{SA^2+IA^2}=\sqrt{SA^2+\left(\dfrac{AD}{2}\right)^2}=\dfrac{a\sqrt{13}}{2}\)
\(SE=\sqrt{SA^2+AE^2}=\sqrt{SA^2+\left(\dfrac{AB}{2}\right)^2}=2a\)
Áp dụng định lý hàm cos trong tam giác SIE:
\(cos\widehat{SIE}=\dfrac{SI^2+IE^2-SE^2}{2SI.IE}=\dfrac{\sqrt{65}}{65}\)
\(\Rightarrow\widehat{SIE}\approx82^052'\)
Đúng 1
Bình luận (0)
2.
a.
\(BB'||AA'\Rightarrow\left(A'D;BB'\right)=\left(A'D;AA'\right)=\widehat{DA'A}\)
\(tan\widehat{DA'A}=\dfrac{DA}{AA'}=\dfrac{2}{\sqrt{5}}\Rightarrow\widehat{DA'A}\approx41^048'\)
b.
\(CD||AB\Rightarrow\left(AC';CD\right)=\left(AC';AB\right)=\widehat{BAC'}\)
\(AC'=\sqrt{AB^2+AD^2+A'A^2}=a\sqrt{10}\)
\(BC'=\sqrt{AD^2+A'A^2}=3a\)
Áp dụng định lý hàm cos cho tam giác BAC':
\(cos\widehat{BAC'}=\dfrac{AC'^2+AB^2-BC'^2}{2AC'.AB}=\dfrac{\sqrt{10}}{10}\)
\(\Rightarrow\widehat{BAC'}\approx71^034'\)
Đúng 1
Bình luận (0)
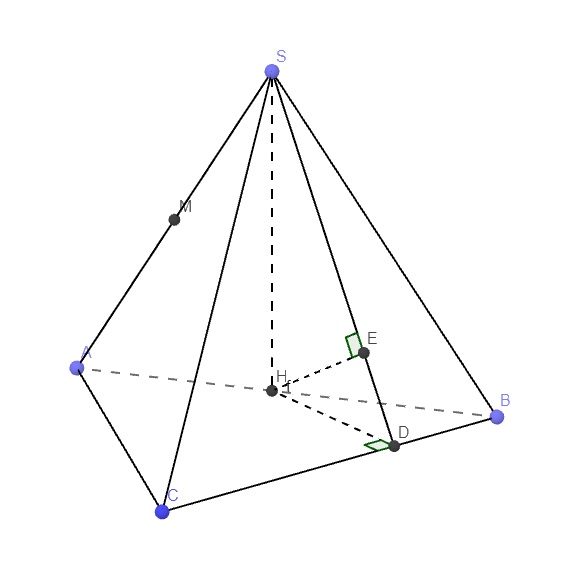
Cho hình chóp S.ABC, đáy ABC là tam giác đều cạnh a. H là trung diểm của AB, SH ⊥ (ABC), SH = a\(\sqrt{3}\) , M là trung điểm SA.
Tính khoảng cách từ M đến mặt phẳng (SBC)
Mọi người giúp em với !!
Do M là trung điểm SA, H là trung điểm AB \(\Rightarrow HM\) là đường trung bình tam giác SAB
\(\Rightarrow HM||SB\Rightarrow HM||\left(SBC\right)\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)\)
Trong mp (ABC) từ H kẻ \(HD\perp BC\), trong mp (SHD) từ H kẻ \(HE\perp SD\)
\(\Rightarrow HE\perp\left(SBC\right)\Rightarrow HE=d\left(H;\left(SBC\right)\right)\)
\(HD=HB.sinB=\dfrac{a}{2}.sin60^0=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng trong tam giác vuông SHD:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HD^2}\Rightarrow HE=\dfrac{SH.HD}{\sqrt{SH^2+HD^2}}=\dfrac{a\sqrt{51}}{17}\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=HE=\dfrac{a\sqrt{51}}{17}\)
Đúng 1
Bình luận (0)
M.n cho em hỏi bài này với ạ,em suy nghĩ mãi mà làm vẫn chưa ra ạ.Mong đc m.n giúp đỡ.Em xin cảm ơn.
cho hình lập phương abcd.a’b’c’d’ có độ dài các cạnh là a. tính khoảng cách giữa 2 đường thẳng bc và c’d
Gọi $O$ là giao điểm của $DC'$ và $D'C$, khi đó $CO=D'O$
Ta có $BC//B'C'$, suy ra $BC//(DB'C')$
Khi đó $d(DC',BC)=d(BC,(DB'C'))=d(C,(DB'C'))$
Lại có $CD\cap (DB'C')=O\Rightarrow \frac{d(C,(DB'C'))}{d(D',(DB'C'))}=\frac{CO}{D'O}=1\Leftrightarrow d(C,(DB'C'))=d(D',(DB'C'))$
Ta có $\left\{\begin{matrix} D'C' \perp B'C' & \\ DD' \perp B'C'& \end{matrix}\right.\Rightarrow B'C' \perp(DD'C')$
Vì $DD'C'C$ là hình vuông nên $D'O \perp DC'$
Ta có: $\left\{\begin{matrix} D'O \perp DC & \\ B'C' \perp(DD'C')\Rightarrow B'C'\perp D'O& \end{matrix}\right.\Rightarrow D'O\perp(DB'C')$
Vậy $D'O=d(D'(DB'C'))$
Áp dụng định lý $Pythagoras$ trong $\Delta D'OD$ ta được:
$DD'^2=DO^2+D'O^2\Leftrightarrow a^2=2D'O^2\Leftrightarrow D'O=\frac{a}{\sqrt{2}}$
Vậy $d(D',(DB'C'))=d(C'(DB'C'))=d(BC,DC')=\frac{a}{\sqrt{2}}$
Đúng 0
Bình luận (0)
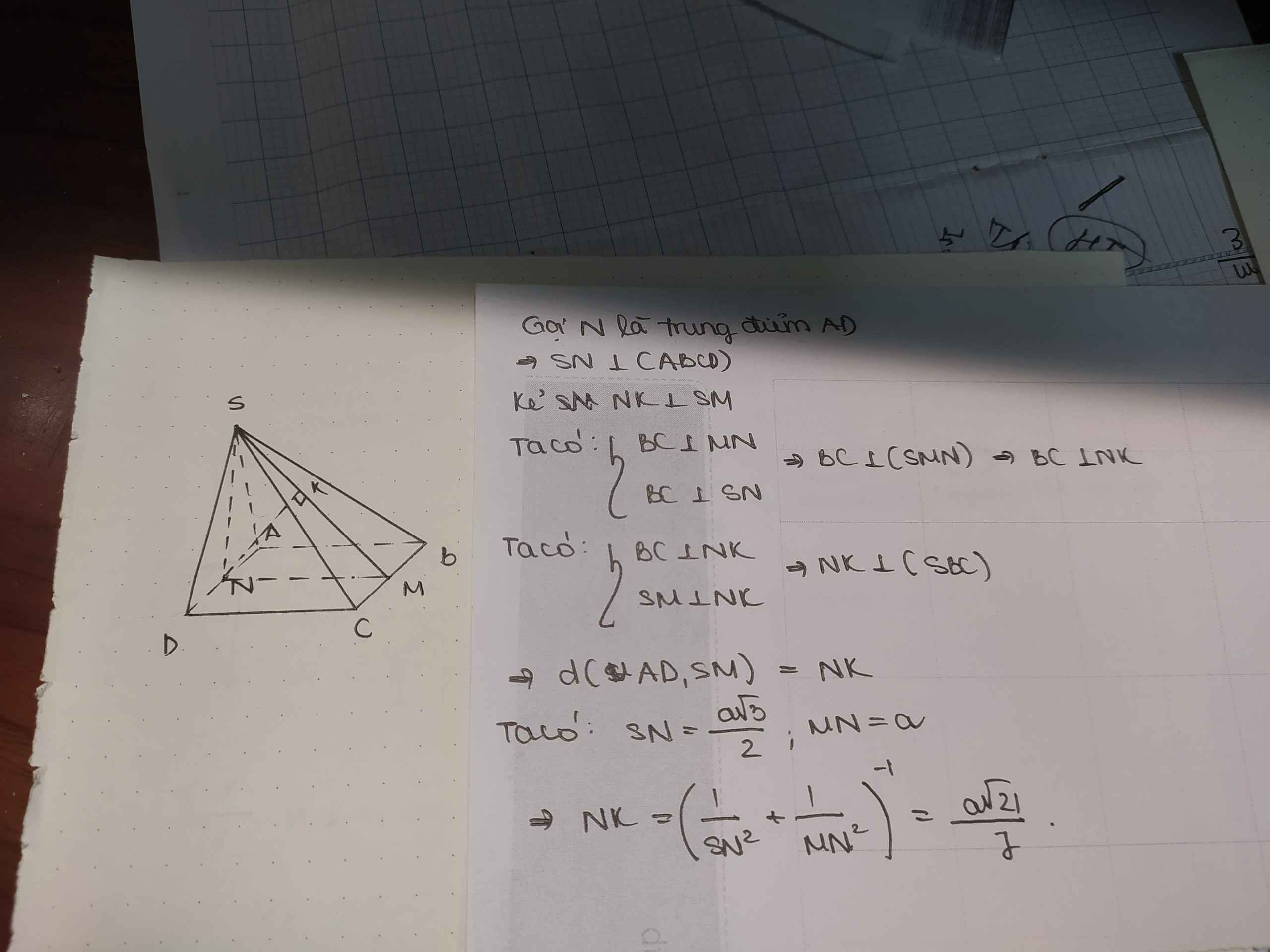
cho hình chóp s.abcd có đáy là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của BC. Tính khoảng cách giữa AD và SM