Bài 5: Công thức nghiệm thu gọn
a)
b) Ta có phương trình hoành độ giao điểm là:
\(-x^2=-3x+2\)
\(\Leftrightarrow x^2-3x+2=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot2=1>0\)
Ta có 2 nghiệm phân biết
Tọa độ giao điểm 1 là:
\(x_1=\dfrac{3+\sqrt{1}}{2}=2\Rightarrow y_1=-2^2=-4\)
Tọa độ giao điểm 2 là:
\(x_2=\dfrac{3-\sqrt{1}}{2}=1\Rightarrow y_2=-1^2=-1\)
Đúng 1
Bình luận (0)
a: Xét tứ giác BKIC có \(\widehat{BKC}=\widehat{BIC}=90^0\)
nên BKIC là tứ giác nội tiếp đường tròn đường kính BC
Tâm O là trung điểm của BC
b: Ta có: BKIC là hình bình hành
=>\(\widehat{CIK}+\widehat{CBK}=180^0\)
mà \(\widehat{CIK}+\widehat{MIC}=180^0\)(hai góc kề bù)
nên \(\widehat{MIC}=\widehat{MBK}\)
Xét ΔMIC và ΔMBK có
\(\widehat{MIC}=\widehat{MBK}\)
\(\widehat{M}\) chung
Do đó: ΔMIC~ΔMBK
=>\(\dfrac{MI}{MB}=\dfrac{MC}{MK}\)
=>\(MB\cdot MC=MI\cdot MK\)
Đúng 0
Bình luận (0)
a) Ta thay lần lượt \(x=60;y=27\) vào \(y=ax+b\)
\(\Rightarrow60a+b=27\)(1)
Ta thay lần lượt \(x=180;y=21\) vào \(y=ax+b\)
\(\Rightarrow180a+b=21\)(2)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}60a+b=27\\180a+b=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{20}\\b=30\end{matrix}\right.\)
\(\Rightarrow y=-\dfrac{1}{20}x+30\)
b) Khi ô tô chạy trên quãng đường dài 700km thì số lít xăng cần đổ thêm là:
\(y=-\dfrac{1}{20}\cdot700+30=-5\)
⇒ Cần đổ thêm 5 lít xăng để xe đi hết quãng đường đó
Đúng 2
Bình luận (0)
Bài 3:
Thay x=1 và y=2 vào (d), ta được:
\(1\left(a-2b\right)+b=2\)
=>a-b=2(1)
Thay x=-4 và y=-3 vào (d), ta được:
-4(a-2b)+b=-3
=>-4a+8b+b=-3
=>-4a+9b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=2\\-4a+9b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a-4b=8\\-4a+9b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5b=5\\a-b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) 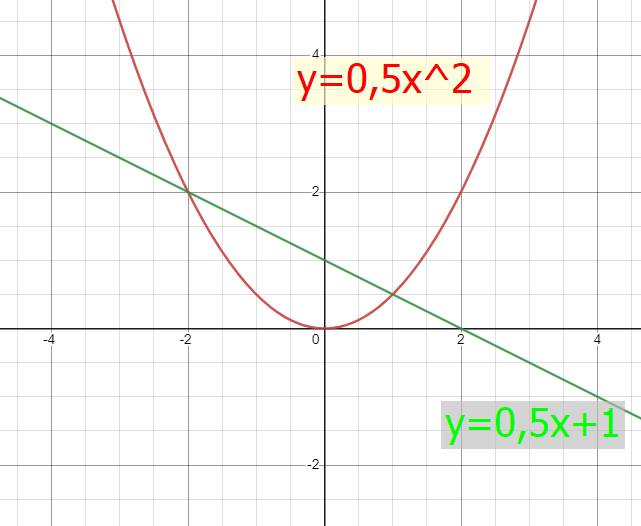
b) Ta có phương trình hoành độ giao điểm của (P) và (d) là:
\(0,5x^2=-0,5x+1\)
\(\Leftrightarrow0,5x^2+0,5x-1=0\)
\(\Leftrightarrow x^2+x-2=0\)
\(\Delta=1^2-4\cdot1\cdot-2=9>0\)
Tọa độ giao điểm 1:
\(x_1=\dfrac{-1+\sqrt{9}}{2}=1\Rightarrow y_1=-0,5\cdot1+1=\dfrac{1}{2}\)
Tọa độ giao điểm 2:
\(x_2=\dfrac{-1-\sqrt{9}}{2}=-2\Rightarrow y_2=-0,5\cdot-2+1=2\)
Đúng 1
Bình luận (0)
Số vòng của cuộn sơ cấp là: \(N_1\) (vòng)
Số vòng của cuộn sơ cấp là: \(N_2=100000-N_1\)(vòng)
Ta có: \(\dfrac{U_2}{U_1}=\dfrac{N_2}{N_1}\)
\(\Rightarrow\dfrac{500000}{1000}=\dfrac{100000-N_1}{N_1}\)
\(\Leftrightarrow500000N_1=1000\left(100000-N_1\right)\)
\(\Leftrightarrow500000N_1=100000000-1000N_1\)
\(\Leftrightarrow501000N_1=100000000\)
\(\Leftrightarrow N_1\approx200\) (vòng)
\(\Rightarrow N_2=100000-200=99800\) (vòng)
Đúng 1
Bình luận (0)