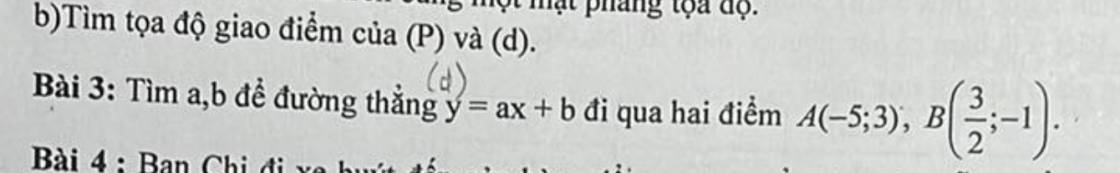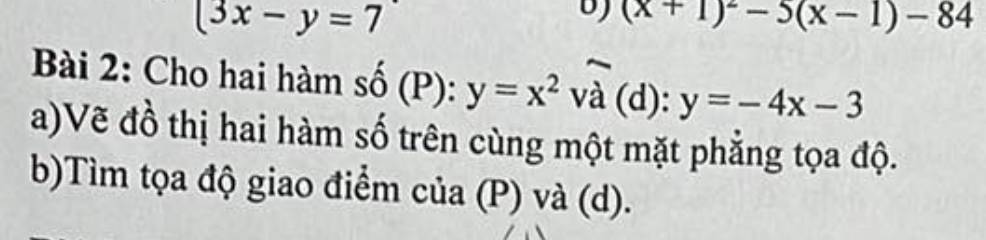Bài 5: Công thức nghiệm thu gọn

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC

\(\widehat{ADC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{MAC}=\widehat{ADC}=\widehat{MDA}\)

Xét ΔMAC và ΔMDA có

\(\widehat{MAC}=\widehat{MDA}\)

\(\widehat{AMC}\) chung

Do đó: ΔMAC~ΔMDA
=>\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\)

=>\(MA^2=MD\cdot MC\)

Lời giải:
Gọi giá nhập vào chiếc ti vi là $a$ (triệu đồng)

Giá niêm yết ban đầu: $a(1+0,4)=1,4a$ ( triệu đồng)

Giá bán khuyến mãi: $1,4a(1-0,15)=1,19a$ (triệu đồng)

Số tiền lời: $1,19a-a=1,9$

$\Leftrightarrow 0,19a=1,9$

$\Leftrightarrow a=10$ (triệu đồng)

Vậy giá nhập là 10 triệu đồng.

Gọi số tiền điện gia đình Bình đã trả trong tháng 3 là x(đồng)

(ĐK: x>0)

Số tiền nước gia đình Bình đã trả trong tháng 3 là:

1075000-x(đồng)

Số tiền điện gia đình Bình đã trả trong tháng 4 là:

\(x\left(1+10\%\right)=1,1x\left(đồng\right)\)

Số tiền nước gia đình Bình đã trả trong tháng 4 là:

\(\left(1+12\%\right)\left(1075000-x\right)=1,12\left(1075000-x\right)\left(đồng\right)\)

Theo đề, ta có phương trình:

1,1x+1,12(1075000-x)=1075000+112500

=>-0,02x+1204000=1187500

=>-0,02x=-16500

=>x=825000(nhận)

Vậy: số tiền điện gia đình Bình đã trả trong tháng 3 là 825000 đồng

số tiền nước gia đình Bình đã trả trong tháng 3 là 1075000-825000=250000 đồng

Bài 4:

a: Đặt y=ax+b

Theo hình, ta sẽ thấy đồ thị hàm số y=ax+b đi qua A(0;12) và B(6;36)

Thay x=0 và y=12 vào y=ax+b, ta được:

\(a\cdot0+b=12\)

=>b=12

=>y=ax+12

Thay x=6 và y=36 vào y=ax+12, ta được:

\(a\cdot6+12=36\)

=>6a=24

=>a=24/6=4

Vậy: a=4; b=12

b: a=4; b=12

=>y=4x+12

Đặt y=84

=>4x+12=84

=>4x=72

=>x=72:4=18

=>Bạn chi mua được 18 quyển tập

Bài 3:

Thay x=-5 và y=3 vào (d), ta được:

\(a\cdot\left(-5\right)+b=3\)

=>-5a+b=3(1)

Thay x=3/2 và y=-1 vào (d), ta được:

\(a\cdot\dfrac{3}{2}+b=-1\)

=>1,5a+b=-1(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}-5a+b=3\\1,5a+b=-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-5a+b-1,5a-b=3-\left(-1\right)\\5a-b=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-6,5a=4\\b=5a+3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=5\cdot\dfrac{-8}{13}+3=\dfrac{-40+39}{13}=-\dfrac{1}{13}\end{matrix}\right.\)

a: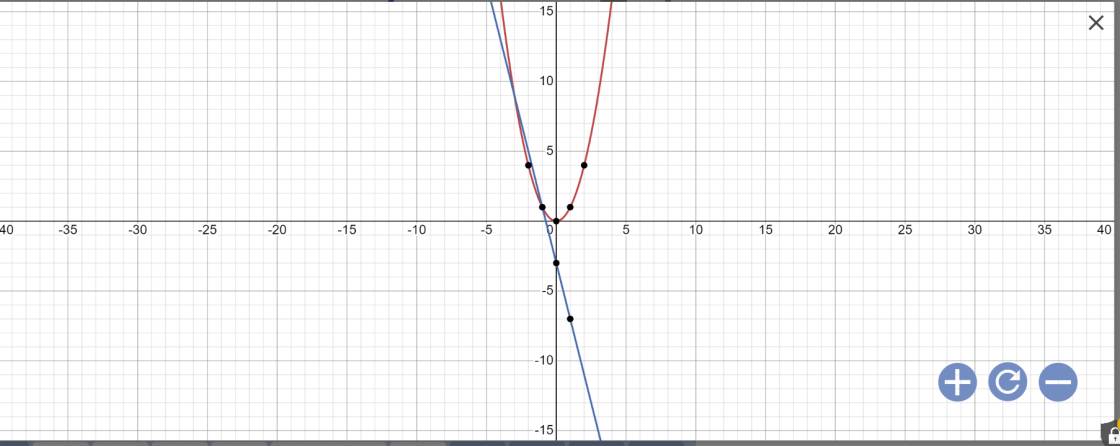 

b: Phương trình hoành độ giao điểm là:

\(x^2=-4x-3\)

=>\(x^2+4x+3=0\)

=>(x+1)(x+3)=0

=>\(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)

Thay x=-1 vào (P), ta được:

\(y=\left(-1\right)^2=1\)

Thay x=-3 vào (P), ta được:

\(y=\left(-3\right)^2=9\)

Vậy: (P) giao (d) tại A(-1;1) và B(-3;9)

a:Δ=(2m-2)^2-4(-m-3)

=4m^2-8m+4+4m+12

=4m^2-4m+16

=(2m-1)^2+15>=15>0

=>Phương trình luôn có hai nghiệm phân biệt

b: Để phương trình có hai nghiệm trái dấu thì -m-3<0

=>m+3>0

=>m>-3

c: Để phương trình có hai nghiệm âm thì:

2m-2<0 và -m-3>0

=>m<1 và m<-3

=>m<-3

d: x1^2+x2^2=(x1+x2)^2-2x1x2

=(2m-2)^2-2(-m-3)

=4m^2-8m+4+2m+6

=4m^2-6m+10

=4(m^2-3/2m+5/2)

=4(m^2-2*m*3/4+9/16+31/16)

=4(m-3/4)^2+31/4>0 với mọi m

a Khi m=1 thì (1) sẽ là x^2+1=0

=>x thuộc rỗng

b: Thay x=1 vào (1),ta được:

1^2-2(m-1)+m^2=0

=>m^2+1-2m+2=0

=>m^2-2m+3=0

=>PTVN

c: Thay x=-3 vào pt, ta được:

(-3)^2-2*(m-1)*(-3)+m^2=0

=>m^2+9+6(m-1)=0

=>m^2+6m+3=0

=>\(m=-3\pm\sqrt{6}\)

a: 3x^2-4x+1=0

a=3; b=-4; c=1

Vì a+b+c=0 nên phương trình có hai nghiệm là:

x1=1 và x2=c/a=1/3

b: -x^2+6x-5=0

=>x^2-6x+5=0

a=1; b=-6; c=5

Vì a+b+c=0 nên phương trình có hai nghiệm là;
x1=1; x2=5/1=5