cho tam giác mnp có 3 góc nhọn (mn
Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
b: Xét tứ giác MNDP có
A là trung điểm của NP
A là trung điểm của MD
Do đó: MNDP là hình bình hành
Suy ra: MN//PD
Đúng 0
Bình luận (2)
cho tam giác MNP có 3 góc nhọn (MN<MP), A là trung điểm của cạnh NP. trên tia MA lấy D sao cho MA=AD.
a) chứng minh rằng tam giác mna= tam giác DPA.
b) chứng minh MN//PD.
c) chứng minh MP=ND.
Đúng 0
Bình luận (0)
Cho góc xoy, lấy góc A thuộc ox , B thuộc oy . Sao cho OA=OB, lấy c thuộc tia phân giác Om
a/Chứng minh △AOM=△OBM
b/ Chững minh AC=BC
C/ Chứng minh Om là đường trung trực của AB
a: Xét ΔAOM và ΔBOM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔAOM=ΔBOM
Đúng 0
Bình luận (0)
Nêu cách nhận biết góc xen giữa.
Giuspe em bài 5 ạa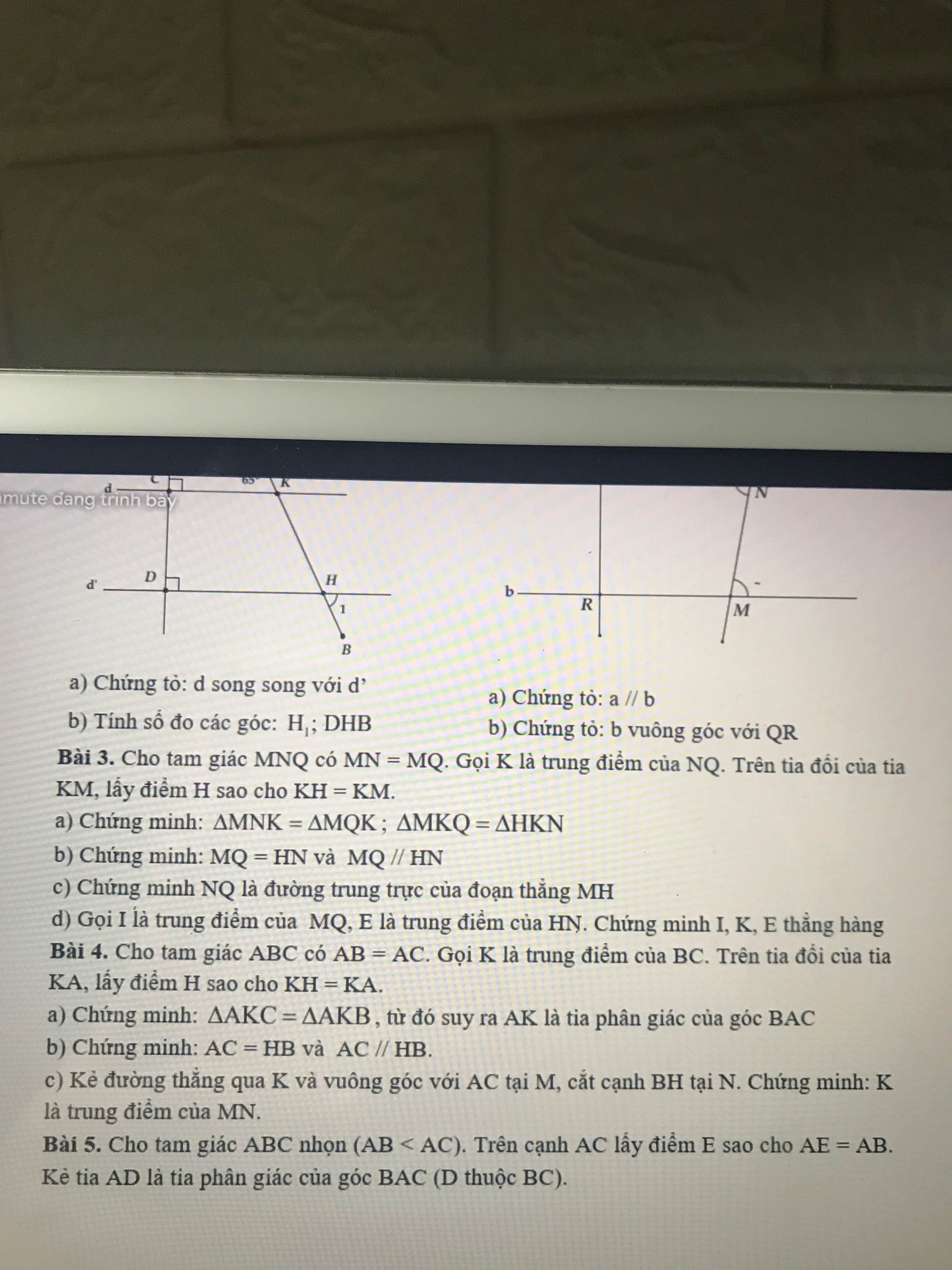
Cho tam giác ABC. Trên tia đối tia AB lấy điểm e sao cho AB=AE. Trên tia đối tia AC lấy điểm D sao cho AC=AD.
a.) CM: BC=DE .
b.) CM: BC//DE.
Mình xin mọi người giúp mình ạ, mình cần gấp.
a: Xét tứ giác BDEC có
A là trung điểm của BE
A là trung điểm của CD
Do đó: BDEC là hình bình hành
Suy ra: BC=DE
Đúng 0
Bình luận (0)
1, Cho DeltaABC(ABBC). AD là tia phân giác của widehat{A}:a, Chứng minh Delta ABDDelta ACDb, Chứng minh BDCD2, Cho Delta ABCperptại A trên cạnh BC là điểm E sao cho BEAB. Kẻ tia phân giác BD của widehat{B}a, Chứng minh Delta ABDDelta EBDb, Tính widehat{DEB}c, Gọi I là giao điểm BD và AE. Chứng minh BDperpAEChú ý: Vẽ hình 2 bài
Đọc tiếp
1, Cho \(\Delta\)ABC(AB=BC). AD là tia phân giác của \(\widehat{A}\):
a, Chứng minh \(\Delta ABD=\Delta ACD\)
b, Chứng minh BD=CD
2, Cho \(\Delta ABC\)\(\perp\)tại A trên cạnh BC là điểm E sao cho BE=AB. Kẻ tia phân giác BD của \(\widehat{B}\)
a, Chứng minh \(\Delta ABD=\Delta EBD\)
b, Tính \(\widehat{DEB}\)
c, Gọi I là giao điểm BD và AE. Chứng minh BD\(\perp\)AE
Chú ý: Vẽ hình 2 bài
a) Nối A và D lại, ta đc: ΔABD & ΔADC
Ta có: D là trung điểm BC => BD=DC
Xét ΔABD & ΔADC có:
AB=AC(gt) ; BD=DC ; AD=AD
=> ΔADB = ΔADC
Đúng 0
Bình luận (0)
1a. Xét △ABD và △ACD có:
\(AB=BC\left(gt\right)\)
\(\hat{BAD}=\hat{CAD}\left(gt\right)\)
\(AD\) chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\)
b/ Từ a suy ra \(BD=CD\) (hai cạnh tương ứng).
2a. Xét △ABD và △EBD có:
\(AB=BE\left(gt\right)\)
\(\hat{ABD}=\hat{EBD}\left(gt\right)\)
\(BD\) chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.g.c\right)\)
b/ Từ a suy ra \(\hat{DEB}=90^o\) (góc tương ứng với góc A).
c/ Xét △ABI và △EBI có:
\(AB=BE\left(gt\right)\)
\(\hat{ABI}=\hat{EBI}\left(do\text{ }\hat{ABD}=\hat{EBD}\right)\)
\(BI\) chung
\(\Rightarrow\Delta ABI=\Delta EBI\left(c.g.c\right)\)
\(\Rightarrow\hat{AIB}=\hat{EIB}=\dfrac{180^o}{2}=90^o\)
Vậy: \(BD\perp AE\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A90. Kẻ tia phân giác của góc B cắt AC tại D.Trên cạnh BC lấy điểm M sao cho BM BA.a) Chứng minh tam giác ABD tam giác MBD.b) Chứng minh rằng AM vuông góc với BD.c) Nếu biết góc AMD36 độ.Tính số đo góc B; của tam giác ABC.
Đọc tiếp
Cho tam giác ABC có góc A=90. Kẻ tia phân giác của góc B cắt AC tại D.
Trên cạnh BC lấy điểm M sao cho BM = BA.
a) Chứng minh tam giác ABD = tam giác MBD.
b) Chứng minh rằng AM vuông góc với BD.
c) Nếu biết góc AMD=36 độ.Tính số đo góc B; của tam giác ABC.
Giúp mình nha,mình xin cảm ơn 🤧
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
IB=IC
Do đó: ΔAIB=ΔAIC
Đúng 0
Bình luận (0)
cho tam giác ABC . gọi M là trung điểm cũa AC trên tia đối của tia MB , lấy điểm d sao cho MB = MD : chứng minh
AD = BC ; AD // BC
vẽ hình nx
Cho 4ABC vuông tại A, trên tia đối của tia CA lấy điểm D sao cho C là trung
điểm AD; trên tia đối của tia CB lấy điểm E sao cho C là trung điểm BE. Chứng minh
a 4ABC = 4DEC và CD ⊥ DE.
b 4BCD = 4ECA.
c BD k AE.




