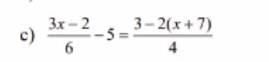Bài 4: Phương trình tích

\(a,x^2+3x-10=0\\ =>x^2+5x-2x-10=0\\ =>x\left(x+5\right)-2\left(x+5\right)=0\\ =>\left(x-2\right)\left(x+5\right)=0\\ =>\left[{}\begin{matrix}x-2=0\\x+5=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ b,2x^2-3x-2=0\\ =>2x^2-x+4x-2=0\\ =>x\left(2x-1\right)+2\left(2x-1\right)=0\\ =>\left(x+2\right)\left(2x-1\right)=0\\ =>\left[{}\begin{matrix}x+2=0\\2x-1=0\end{matrix}\right.=>\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\end{matrix}\right.\)

1: =>(x+5)(x-2)=0

=>x=2 hoặc x=-5

2:=>2x^2-4x+x-2=0

=>(x-2)(2x+1)=0

=>x=2 hoặc x=-1/2

\(1,x^2+3x-10=0\)

\(\Leftrightarrow x^2-2x+5x-10=0\)

\(\Leftrightarrow x\left(x-2\right)+5\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)

\(2,2x^2-3x-2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\left(x+2\right)^3-16\left(x+2\right)=0\)

\(\Rightarrow\left(x+2\right)\left[\left(x+2\right)^2-16\right]=0\)

\(\Rightarrow\left(x+2\right)\left(x+2-4\right)\left(x+2+4\right)=0\)

\(\Rightarrow\left(x+2\right)\left(x-2\right)\left(x+6\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x-2=0\\x+6=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\\x=-6\end{matrix}\right.\)

Vậy \(S=\left\{-2;2;-6\right\}\)

\(2x^3-6x^2+12x-8=0\)

\(\Rightarrow2x^3-2x^23+3.2^2-2^3=0\)

\(\Rightarrow\left(x-2\right)^3=0\)

\(\Rightarrow x-2=0\)

\(\Rightarrow x=2\)

giải giúp mình với

Thay \(t=3\) vào pt trên :

\(\Rightarrow\dfrac{2}{5-3}-a-3=2a\left(a+2\right)\)

\(\Rightarrow1-a-3-2a^2-4a=0\)

\(\Rightarrow-2a^2-5a+1=0\)

\(\Rightarrow\left\{{}\begin{matrix}a_1=\dfrac{-5+\sqrt{33}}{4}\\a_2=\dfrac{-5-\sqrt{33}}{4}\end{matrix}\right.\)

Thay \(t=3\) vào pt trên :

\(\Rightarrow\dfrac{2}{5-3}-a-3=2a\left(a+2\right)\)

\(\Rightarrow21-a-3-2a^2-4a=0\)

\(\Rightarrow-2a^2-5a+18=0\)

\(\Rightarrow\left\{{}\begin{matrix}a_1=2\\a_2=-\dfrac{9}{2}\end{matrix}\right.\)

Vậy để pt có \(t=-3\) là nghiệm thì \(a=2\) và \(a=-\dfrac{9}{2}\)

\(9\left(x-3\right)^2=4\left(x+2\right)^2\\ =>9\left(x^2-6x+9\right)=4\left(x^2+4x+4\right)\\ =>9x^2-54x+81-4x^2-16x-16=0\\ =>5x^2-70x+65=0\\ =>5x^2-5x-65x+65=0\\ =>5x\left(x-1\right)-65\left(x-1\right)=0\\ =>\left(5x-65\right)\left(x-1\right)=0\\ =>\left[{}\begin{matrix}x-1=0\\5x-65=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=1\\x=13\end{matrix}\right.\)

=x^2+4x+4+(4x-3)(x+2)

=x^2+4x+4+4x^2+8x-3x-6

=5x^2+9x-2

\(\left(x+2\right)^2-\left(x+2\right)\left(3-4x\right)\)

\(=\left(x+2\right)\left(x+2-3+4x\right)\)

\(=\left(x+2\right)\left(5x-1\right)\)

đề bài?

=x^3+x^2+7x^2+7x+2x+2

=(x+1)(x^2+7x+2)

\(\left(x-3\right)^2=\left(3x-2\right)^2\)

\(\Rightarrow x-3=3x-2\)

\(\Rightarrow x-3x=-2+3\)

\(\Rightarrow-2x=1\)

\(\Rightarrow x=-\dfrac{1}{2}\)

\(\left(2x+7\right)^2=\left(x+3\right)^2\)

\(\Rightarrow2x+7=x+3\)

\(\Rightarrow2x-x=3-7\)

\(\Rightarrow x=-4\)

a: (3x-2)^2=(x-3)^2

=>3x-2=x-3 hoặc 3x-2=3-x

=>2x=-1 hoặc 4x=5

=>x=5/4 hoặc x=-1/2

b: (2x+7)^2=(x+3)^2

=>2x+7=x+3 hoặc 2x+7=-x-3

=>x=-4 hoặc x=-10/3

`B4:`

`a)` Thay `x=3` vào ptr:

  `3^3-3^2-9.3-9m=0<=>m=-1`

`b)` Thay `m=-1` vào ptr có: `x^3-x^2-9x+9=0`

        `<=>x^2(x-1)-9(x-1)=0`

        `<=>(x-1)(x-3)(x+3)=0<=>[(x=1),(x=+-3):}`

`B5:`

`a)` Thay `x=-2` vào có: `(-2)^3-(m^2-m+7).(-2)-3(m^2-m-2)=0`

    `<=>-8+2m^2-2m+14-3m^2+3m+6=0`

   `<=>-m^2+m+12=0<=>(m-4)(m+3)=0<=>[(m=4),(m=-3):}`

`b)`

`@` Với `m=4` có: `x^3-(4^2-4+7)x-3(4^2-4-2)=0`

      `<=>x^3-19x-30=0`

      `<=>x^3-5x^2+5x^2-25x+6x-30=0`

      `<=>(x-5)(x^2+5x+6)=0`

      `<=>(x-5)(x+2)(x+3)=0<=>[(x=5),(x=-2),(x=-3):}`

`@` Với `m=-3` có: `x^3-[(-3)^2-(-3)+7]x-3[(-3)^2-(-3)-2]=0`

   `<=>x^3-19x-30=0<=>[(x=5),(x=-2),(x=-3):}`

\(\dfrac{3x-2}{6}-5=\dfrac{3-2\left(x+7\right)}{4}\)

\(< =>\dfrac{6x-4}{12}-\dfrac{60}{12}=\dfrac{9-6\left(x+7\right)}{12}\)

\(< =>6x-4-60=9-6x-42\)

\(< =>6x+6x=9-42+4+60\)

\(< =>12x=31\\ < =>x=\dfrac{31}{12}\)

vậy \(S=\dfrac{31}{12}\)

=>(x-6)^4+(x-8)^4=16

Đặt a=x-7

=>(a-1)^4+(a+1)^4=16

=>a^4+4a^3+6a^2+4a+1+a^4-4a^3+6a^2-4a+1=16

=>2a^4+12a^2-14=0

=>a^4+6a^2-7=0

=>(a^2+7)(a^2-1)=0

=>a^2=1

=>a=1 hoặc a=-1

=>x-7=1 hoặc x-7=-1

=>x=6 hoặc x=8