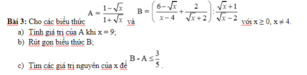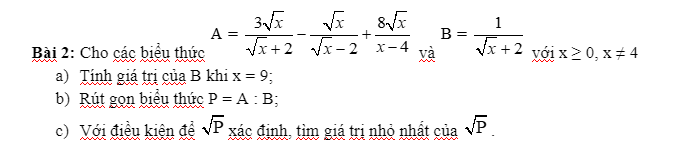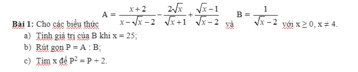Bài 4: Công thức nghiệm của phương trình bậc hai

a: 2k^2+kx-10=0

Khi x=2 thì ta sẽ có: 2k^2+2k-10=0

=>k^2+k-5=0

=>\(k=\dfrac{-1\pm\sqrt{21}}{2}\)

b: Khi x=-2 thì ta sẽ có:

\(\left(-2k-5\right)\cdot4-\left(k-2\right)\cdot\left(-2\right)+2k=0\)

=>-8k-20+2k-4+2k=0

=>-4k-24=0

=>k=-6

c: Theo đề, ta có:

9k-3k-72=0

=>6k=72

=>k=12

a: \(\Delta=2^2-4\cdot1\cdot\left(-30\right)=124\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-2-2\sqrt{31}}{2}=-1-\sqrt{31}\\x_2=-1+\sqrt{31}\end{matrix}\right.\)

b: \(2x^2-3x-5=0\)

\(\Leftrightarrow2x^2-5x+2x-5=0\)

=>(2x-5)(x+1)=0

=>x=5/2 hoặc x=-1

a.\(x^2+2x-30=0\)

\(\Delta=2^2-4.\left(-30\right)=4+120=124>0\)

=> pt có 2 nghiệm

\(\left\{{}\begin{matrix}x=\dfrac{-2+\sqrt{124}}{2}=\dfrac{-2+2\sqrt{31}}{2}=-1+\sqrt{31}\\x=\dfrac{-2-\sqrt{124}}{2}=-1-\sqrt{31}\end{matrix}\right.\)

b.\(2x^2-3x-5=0\)

Ta có: a-b+c=0

\(\Rightarrow\left\{{}\begin{matrix}x=-1\\x=\dfrac{5}{2}\end{matrix}\right.\)( vi-ét )

vô nghiệm

\(\text{Δ}=\left(-2\right)^2-4\cdot3\cdot3=4-4\cdot9< 0\)

Do đó: Phương trình vô nghiệm

vô nghiệm

x=1

\(2x^2-4x+2=0\)

\(\Leftrightarrow2\left(x^2-2x+1\right)=0\)

\(\Leftrightarrow\left(x-1\right)^2=0\)

\(\Leftrightarrow x-1=0\)

\(\Leftrightarrow x=1\)

Vậy....

\(\Delta'=4-2.2=0\)vậy pt có nghiệm kép 

\(x_1=x_2=\dfrac{4}{2}=2\)

a: Khi m=1 thì phương trình sẽ là \(x^2-3x-5=0\)

\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-5\right)=9+20=29\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{29}}{2}\\x_2=\dfrac{3+\sqrt{29}}{2}\end{matrix}\right.\)

b: \(\text{Δ}=\left(2m+1\right)^2-4\left(-m-4\right)\)

\(=4m^2+4m+1+4m+16\)

\(=4m^2+8m+17\)

\(=4m^2+4m+4+13\)

\(=\left(2m+2\right)^2+13>0\)

Do đó: Phương trình luôn có hai nghiệm phân biệt

a, Thay m =1 ta đc 

\(x^2-3x-5=0\)

\(\Delta=9-4\left(-5\right)=9+20=29>0\)

Vậy pt luôn có 2 nghiệm pb 

\(x=\dfrac{3\pm\sqrt{29}}{2}\)

b, Ta có \(\Delta=\left(2m+1\right)^2-4\left(-m-4\right)=4m^2+4m+1+4m+16\)

\(=4m^2+8m+16+1=4\left(m^2+2m+4\right)+1=4\left(m+1\right)^2+13>0\)

vậy pt luôn có 2 nghiệm pb 

a, Thay m=1 vào pt ta có:
\(x^2-\left(2.1+1\right)x-1-4=0\\ \Leftrightarrow x^2+3x-5=0\)

\(\Delta=3^2-4.1.\left(-5\right)=9+20=29\)

\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{29}}{2}\\x_2=\dfrac{-3+\sqrt{29}}{2}\end{matrix}\right.\)

b, Ta có: 

\(\Delta=\left[-\left(2m+1\right)\right]^2-4.1.\left(-m-4\right)\\=\left(2m+1\right)^2+4\left(m+4\right)\\ =4m^2+4m+1+4m+16\\ =4m^2+8m+17\\ =4\left(m^2+2m+1\right)+13\\ =4\left(m+1\right)^2+13>0 \)

Vậy pt luôn có 2 nghiệm phân biệt

2;3;6

Gọi a,b,c là ba số tự nhiên cần tìm. Điều kiện: a<b<c và 1≠a,b,c∈N*.

Từ điều kiện, ta có \(\dfrac{1}{a}>\dfrac{1}{b}>\dfrac{1}{c}\).

Ta có: \(\dfrac{3}{c}< \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1< \dfrac{3}{a}\), suy ra \(c>3>a\). Suy ra, chỉ có a=2 thỏa mãn.

Đặt c=2+k với k∈N và k>1.

Ta có: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2}+\dfrac{1}{b}+\dfrac{1}{2+k}=1\) \(\Leftrightarrow\) \(\dfrac{1}{2}-\dfrac{1}{2+k}=\dfrac{1}{b}\) \(\Leftrightarrow\) \(b=\dfrac{2k+4}{k}=2+\dfrac{4}{k}\).

Do 1≠b∈N* nên k=Ư(4)={-4,-2,-1,1,2,4}.

+) Với k={-4,-2,-1,1} (loại, k>1).

+) Với k=2, c=4 và b=4 (loại, a<b<c).

+) Với k=4, c=6 và b=3 (nhận).

Vậy ba số tự nhiện cần tìm là 2, 3 và 6.

a: Thay x=9 vào A, ta được:

\(A=\dfrac{1-3}{1+3}=\dfrac{-2}{4}=-\dfrac{1}{2}\)

b: \(B=\dfrac{6-\sqrt{x}+2\sqrt{x}-4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+1}\)

a, Thay x = 9 vào B ta có:

\(B=\dfrac{1}{\sqrt{9}+2}=\dfrac{1}{3+2}=\dfrac{1}{5}\)

b, ta có : pt tương đương của P:

\(\left(\dfrac{3\sqrt{x}}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{8\sqrt{x}}{x-4}\right).\left(\dfrac{\sqrt{x}+2}{1}\right)\)

dkxd: x khác -2 ; x khác 4 

\(\Leftrightarrow\left(\dfrac{3\sqrt{x}}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{8\sqrt{x}}{x-4}\right).\sqrt{x}+2\)

\(P=............\)

a: Thay x=9 vào B, ta được

\(B=\dfrac{1}{3+2}=\dfrac{1}{5}\)

b: \(P=\dfrac{3x-6\sqrt{x}-x-2\sqrt{x}+8\sqrt{x}}{x-4}\cdot\dfrac{\sqrt{x}+2}{1}\)

\(=\dfrac{2x}{\sqrt{x}-2}\)

c: Để \(\sqrt{P}\) xác định thì P>=0

=>2x>=0

hay x>=0

Kết hợp ĐKXĐ, ta được: x>=0; x<>4

đầy đủ hơn nek:

Lời giải:

a. Khi $x=25$ thì $B=\frac{1}{\sqrt{25}-2}=\frac{1}{5-2}=\frac{1}{3}$

b. \(A=\frac{x+2}{(\sqrt{x}+1)(\sqrt{x}-2)}-\frac{2\sqrt{x}(\sqrt{x}-2)}{(\sqrt{x}+1)(\sqrt{x}-2)}+\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}-2)(\sqrt{x}+1)}\)

\(=\frac{x+2-2x+4\sqrt{x}+x-1}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{4\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}\)

\(\Rightarrow P=A:B=\frac{4\sqrt{x}+1}{\sqrt{x}+1}\)

Từ đây suy ra $P>0$

c.

\(P^2=P+2\Leftrightarrow P^2-P-2=0\Leftrightarrow (P+1)(P-2)=0\)

$\Leftrightarrow P=2$ (do $P>0$)

$\Leftrightarrow \frac{4\sqrt{x}+1}{\sqrt{x}+1}=2$

$\Leftrightarrow 4\sqrt{x}+1=2\sqrt{x}+2$

$\Leftrightarrow 2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}$ (tm)