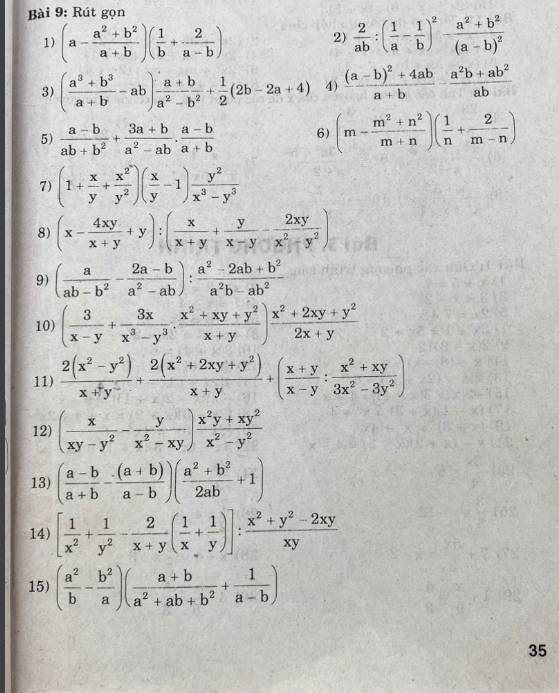Cho biểu thức: x^2+6x+9/x+3 a) Rút gọn biểu thức A b) Tính giá trị của a tại x=-2
Bài 3: Rút gọn phân thức
\(a,\dfrac{x^2+6x+9}{x+3}\\ đk:x\ne-3\\ =\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
b, Thay \(x=-2\left(t/mđk\right)\) vào
\(-2+3=1\)
Vậy tại \(x=-2\) thì biểu thức = 1
Đúng 2
Bình luận (1)
\(A=\dfrac{x^2+6x+9}{x+3}\)
\(A=\dfrac{x^2+2.x.3+3^2}{x+3}\)
\(A=\dfrac{\left(x+3\right)^2}{x+3}\)
\(A=x+3\)
b) Thay x = -2 vào A ta được A = -2 + 3 = 1
Vậy khi x = -2 thì A = 1
Đúng 1
Bình luận (2)
\(a)\dfrac{x^2+6x+9}{x+3}=\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
\(\text{b)Thay x=-2 vào biểu thức x+3,ta được:}\)
\(x+3=\left(-2\right)+3=1\)
\(\text{Vậy giá trị của biểu thức trên tại x=-2 là:1}\)
Đúng 0
Bình luận (0)
X²-4/x+2
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+2}=x-2\)
Đúng 0
Bình luận (0)
\(\dfrac{8x^2+16x^2+8x}{4x^2+4x}\)
giúp với mn ơi
\(\dfrac{8x^2+16x^2+8x}{4x^2+4x}\)
= \(\dfrac{24x^2+8x}{4x^2+4x}\)
= \(\dfrac{4x(6x+2)}{4x(x+1)}\)
= \(\dfrac{6x+2}{x+1}\)
Đúng 2
Bình luận (0)
\(\dfrac{8x^2+16x^2+8x}{4x^2+4x}\\ =\dfrac{8x\left(x+2x+1\right)}{4x\left(x+1\right)}\\ =\dfrac{2\left(x+2x+1\right)}{x+1}\)
Đúng 1
Bình luận (0)
Giúp mình giải bài này với ạ
rút gọn (2x-3)(4x^2+6x+9)-4x(2x^2-1)
\(\left(2x-3\right)\left(4x^2+6x+9\right)-4x\left(2x^2-1\right)\)
\(=8x^3-27-8x^3+4x\\ =8x^3-8x^3+4x-27\\ =4x-27\)
Đúng 3
Bình luận (1)
bài 9 cho phân thức M = \(\dfrac{11x^2+11x}{x^2-1}\)
a, rút gọn phân thức M
b, tìm giá trị nguyên của x để M có giá trị nguyên![]()
giúp em mới ạ
a. \(M=\dfrac{11x^2+11x}{x^2-1}\left(đk:x\ne\pm1\right)\)
\(=\dfrac{11x\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{11x}{x-1}\)
b. \(\dfrac{11x}{x-1}=x.\dfrac{11}{x-1}\)
\(M\in Z\Leftrightarrow x.\dfrac{11}{x-1}\in Z\Leftrightarrow\dfrac{11}{x-1}\in Z\) (vì x nguyên)
\(\Leftrightarrow x-1\inƯ_{\left(11\right)}=\left\{\pm1;\pm11\right\}\)
+) \(x-1=1\Leftrightarrow x=2\)
+) \(x-1=-1\Leftrightarrow x=0\)
+) \(x-1=11\Leftrightarrow x=12\)
+) \(x-1=-11\Leftrightarrow x=-10\)
Đúng 0
Bình luận (0)
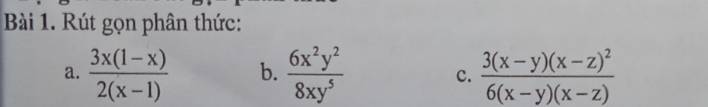
giai chi tiet nhe
a,=\(\dfrac{-3x\left(x-1\right)}{2\left(x-1\right)}=\dfrac{-3x}{2}\)
Đúng 0
Bình luận (0)
Giúp mình làm bài 1 2 3 đề 2 3 4 môn toán




Bài 3:
a: \(\Leftrightarrow2x^2-10x+x-5-2x^2=-10\)
=>-9x-5=-10
=>-9x=-5
=>x=5/9
b: \(\Leftrightarrow\left(x-5-7\right)\left(x-5+7\right)=0\)
=>(x-12)(x+2)=0
=>x=12 hoặc x=-2
Bài 2:
a: =5x*x-5x*3
=5x(x-3)
b: =(x+3)^2-4y^2
=(x+3+2y)(x+3-2y)
Đúng 0
Bình luận (0)
Bài 2:
a: \(=\dfrac{-x-1+2x-2-x+5}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{1-2x}\)
\(=\dfrac{2}{1-2x}=\dfrac{-2}{2x-1}\)
b: Để C là số nguyên thì \(2x-1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)
Bài 3:
a: \(A=\left(\dfrac{-\left(x-2\right)}{x+3}+\dfrac{x-3}{x+2}+\dfrac{2-x}{\left(x+2\right)\left(x+3\right)}\right):\dfrac{x-1-x}{x-1}\)
\(=\dfrac{-x^2+4+x^2-9+2-x}{\left(x+3\right)\left(x+2\right)}\cdot\dfrac{x-1}{-1}\)
\(=\dfrac{-x+3}{\left(x+3\right)\left(x+2\right)}\cdot\dfrac{1-x}{1}=\dfrac{x-1}{x+2}\)
b: Để A=0 thì x-1=0
=>x=1(loại)
c: Để A>0 thì x-1/x+2>0
=>x>1 hoặc x<-2
Đúng 0
Bình luận (0)
Rút gọn phân thức
\(\dfrac{\left(x-2\right)^2\left(2x+2x^2\right)}{\left(x+1\right)\left(4x-x^3\right)}\)
\(\dfrac{\left(x-2\right)^2\left(2x+2x^2\right)}{\left(x+1\right)\left(4x-x^3\right)}\\ =\dfrac{\left(x-2\right)^22x\left(1+x\right)}{\left(x+1\right)x\left(4-x^2\right)}\\ =\dfrac{2\left(x-2\right)^2}{\left(2-x\right)\left(2+x\right)}\\ =\dfrac{2\left(2-x\right)^2}{\left(2-x\right)\left(2+x\right)}\\ =\dfrac{2\left(2-x\right)}{2+x}\)
Đúng 2
Bình luận (0)