
Bài 3: Rút gọn phân thức
\(b,\dfrac{2xy^2\left(5y-3x\right)}{4x^2y\left(3x-5y\right)^2}=\dfrac{-2xy^2\left(3x-5y\right)}{4x^2y\left(3x-5y\right)^2}=\dfrac{-y}{2x\left(3x-5y\right)}\)
Đúng 0
Bình luận (0)
5) (a²ˣ - b²ˣ)/(aˣ + bˣ)
= (aˣ - bˣ)(aˣ + bˣ)/(aˣ + bˣ)
= aˣ - bˣ
Đúng 1
Bình luận (0)
Giúp ạ 
\(=\dfrac{2xy\cdot y\left(5y-3x\right)}{2xy\cdot x\cdot\left(5y-3x\right)^2}=\dfrac{y}{x\left(5y-3x\right)}\)
Đúng 1
Bình luận (0)
Bài10:
a: \(\dfrac{\left(x-2\right)\left(2x^2+2x\right)}{\left(x+1\right)\left(4x-x^3\right)}\)
\(=\dfrac{2x\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)\left(4-x^2\right)}\)
\(=\dfrac{2\left(x-2\right)}{\left(2-x\right)\left(2+x\right)}=\dfrac{-2}{x+2}\)
b: \(\dfrac{x^2+y^2+2xy-1}{x^2-y^2+1+2x}\)
\(=\dfrac{\left(x+y\right)^2-1}{\left(x+1\right)^2-y^2}=\dfrac{\left(x+y+1\right)\left(x+y-1\right)}{\left(x+1+y\right)\left(x+1-y\right)}\)
\(=\dfrac{x+y-1}{x-y+1}\)
c: \(\dfrac{\left(x^2+2\right)^2-4x^2}{y\left(x^2+2\right)-2xy-\left(x-1\right)^2-1}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{y\left(x^2+2-2x\right)-\left(x^2-2x+2\right)}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{\left(x^2-2x+2\right)\left(y-1\right)}=\dfrac{x^2+2x+2}{y-1}\)
d: \(\dfrac{3y-2-3xy+2x}{1-3x-x^3+3x^2}\)
\(=\dfrac{3y-2-x\left(3y-2\right)}{\left(1-x\right)\left(1+x+x^2\right)+3x\left(x-1\right)}\)
\(=\dfrac{\left(3y-2\right)\left(1-x\right)}{\left(1-x\right)\left(1+x+x^2-3x\right)}\)
\(=\dfrac{3y-2}{x^2-2x+1}=\dfrac{3y-2}{\left(x-1\right)^2}\)
Đúng 1
Bình luận (0)
(x^(3)-4x^(2)-x+4)/(x^(3)-7x^(2)+14x-8)=(x+1)/(x+2)
\(\dfrac{x^3-4x^2-x+4}{x^3-7x^2+14x-8}\)
\(=\dfrac{x^2\cdot\left(x-4\right)-\left(x-4\right)}{\left(x-2\right)\left(x^2+2x+4\right)-7x\left(x-2\right)}\)
\(=\dfrac{\left(x-4\right)\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x^2-5x+4\right)}\)
\(=\dfrac{x+1}{x-2}\)
Đúng 0
Bình luận (0)
Rút gọn phân số
x^3-4x^2-x+4/x^3-7x^2+14x-8
\(=\dfrac{x^2\left(x-4\right)-\left(x-4\right)}{\left(x-2\right)\left(x^2+2x+4\right)-7x\left(x-2\right)}\)
\(=\dfrac{\left(x-4\right)\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x-1\right)\left(x-4\right)}=\dfrac{x+1}{x-2}\)
Đúng 1
Bình luận (0)
27a^3+b^3/ 3ab+b^2
\(\dfrac{27a^3+b^3}{3ab+b^2}\\ =\dfrac{\left(3a+b\right)\left(9a^2-3ab+b^2\right)}{b\left(3a+b\right)}\\ =\dfrac{9a^2-3ab+b^2}{b}\)
Đúng 1
Bình luận (0)
\(=\dfrac{\left(3a+b\right)\left(9a^2-3ab+b^2\right)}{b\left(3a+b\right)}=\dfrac{9a^2-3ab+b^2}{b}\)
Đúng 1
Bình luận (0)
X^4-1/(x^2-1)(x+2)
\(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)}{\left(x^2-1\right)\left(x+2\right)}=\dfrac{x^2+1}{x+2}\)
Đúng 0
Bình luận (0)
\(\dfrac{x^4-1}{\left(x^2-1\right)\left(x+2\right)}\\ =\dfrac{\left(x^2-1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}\\ =\dfrac{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}\\ =\dfrac{x^2+1}{x+2}\)
Đúng 0
Bình luận (0)
X^3-x^2-x+1/x^4-2x^2+1
\(=\dfrac{x^2\left(x-1\right)-\left(x-1\right)}{\left(x^2-1\right)^2}=\dfrac{x-1}{x^2-1}=\dfrac{1}{x+1}\)
Đúng 1
Bình luận (0)
\(\dfrac{x^3-x^2-x+1}{x^4-2x^2+1}\\ =\dfrac{x^2\left(x-1\right)-\left(x-1\right)}{\left(x^2-1\right)^2}\\ =\dfrac{\left(x-1\right)\left(x^2-1\right)}{\left(x^2-1\right)^2}\\ =\dfrac{x-1}{x^2-1}\\ =\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{1}{x+1}\)
Đúng 1
Bình luận (0)
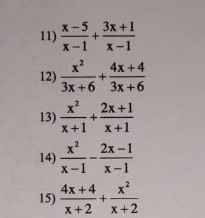
Tính và rút gọn
11: \(=\dfrac{x-5+3x+1}{x-1}=\dfrac{4x-4}{x-1}=4\)1
12: \(=\dfrac{x^2+4x+4}{3\left(x+2\right)}=\dfrac{x+2}{3}\)
13: \(=\dfrac{x^2+2x+1}{x+1}=x+1\)
14: \(=\dfrac{x^2-2x+1}{x-1}=x-1\)
15: \(=\dfrac{x^2+4x+4}{x+2}=x+2\)
Đúng 1
Bình luận (0)







