Các bạn ơi giúp mình với
Bài 3: Nhị thức Niu-tơn
giá trị của biểu thức \(C=C^0_n-\dfrac{1}{3}C^1_n+\dfrac{1}{3^2}C^2_n-...+\left(-1\right)^n.\left(\dfrac{1}{3^n}\right)C^{^n}_n\)
Mọi người giúp em chọn trắc nghiệm với câu 13 tự luận với ạa, em cảm ơn:(
Đọc tiếp


Mọi người giúp em chọn trắc nghiệm với câu 13 tự luận với ạa, em cảm ơn:(
c: Số hạng tổng quát là:
\(C^k_{10}\cdot\left(2x^2\right)^{10-k}\cdot\left(-\dfrac{1}{3}\right)^k\left(0< =k< =10\right)\)
\(=C^k_{10}\cdot2^{10-k}\cdot x^{20-2k}\cdot\left(-\dfrac{1}{3}\right)^k\)
Số hạng chứa x^10 là số hạng có 20-2k=10
=>k=5
=>Số hạng đó là \(C^5_{10}\cdot2^{10-5}\cdot\left(-\dfrac{1}{3}\right)^5\cdot x^{10}=-\dfrac{896}{27}x^{10}\)
Số hạng chứa x^16 là khi 20-2k=16
=>k=2
=>Số hạng đó là \(C^2_{10}\cdot2^8\cdot\left(-\dfrac{1}{3}\right)^2\cdot x^{16}=C^2_{10}\cdot\dfrac{256}{9}x^{16}\)
Số hạng chứa x^6 là khi 20-2k=6
=>k=7
=>Số hạng đó là \(C^7_{10}\cdot2^3\cdot\left(-\dfrac{1}{3}\right)^7\cdot x^6\)
d: \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
Số hạng tổng quát là \(C^k_{12}\cdot\left(\dfrac{x}{3}\right)^{12-k}\cdot\left(-\dfrac{3}{x}\right)^k\)
\(=C^k_{12}\cdot\dfrac{x^{12-k}}{3^{12-k}}\cdot\dfrac{\left(-3\right)^k}{x^k}=C^k_{12}\cdot\dfrac{\left(-3\right)^k}{3^{12-k}}\cdot x^{12-2k}\)
Số hạng chứa x^4 thì 12-2k=4
=>2k=8
=>k=4
=>Số hạng đó là \(C^4_{12}\cdot\dfrac{\left(-3\right)^4}{3^8}=C^4_{12}\cdot\dfrac{1}{3^4}\)
\(\left(x+\dfrac{2}{x^2}\right)^7\)
Số hạng tổng quát là: \(C^k_7\cdot x^{7-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_7\cdot x^{7-k}\cdot\dfrac{2^k}{x^{2k}}=C^k_7\cdot2^k\cdot x^{7-3k}\)
Số hạng chứa x^4 thì 7-3k=4
=>3k=3
=>k=1
=>Hệ số là \(C^1_7\cdot2^1=7\cdot2=14\)
Đúng 1
Bình luận (0)
cho đa thức p(x)=(1+x)^9+(1+x)^10+..+(1+x)^14 có dạng khai triển là P(x)=a0+a1x+a2x^2+...+a14x^14. Tìm hệ số a9
\(\left(1+x\right)^n=\sum\limits^n_{k=0}C_n^kx^k\) có hệ số số hạng chứa \(x^9\) dạng \(C_n^9\)
Do đó \(a_9=C_9^9+C_{10}^9+...+C_{14}^9=...\)
Đúng 2
Bình luận (0)
cho k, n ∈ Z+ , k≤n. CMR :
Cn0.Cnk +Cn1.Cnk+1+...+ Cnn-k.Cnn= C2nn+k
10, 11

10
Xét khai triển:
\(\left(x+2\right)^{2013}=C_{2013}^0.2^{2013}+C_{2013}^1x.2^{2012}+C_{2013}^2x^22^{2011}+...+C_{2013}^{2013}x^{2013}\)
Đạo hàm 2 vế:
\(2013\left(x+2\right)^{2012}=C_{2013}^12^{2012}+2C_{2013}^2x.2^{2011}+...+2013C_{2013}^{2013}x^{2012}\)
\(\Rightarrow2013x\left(x+2\right)^{2012}=xC_{2013}^12^{2012}+2C_{2013}^2x^2.2^{2011}+...+2013C_{2013}^{2013}x^{2013}\)
Tiếp tục đạo hàm 2 vế:
\(2013\left(x+2\right)^{2012}+2012.2013x\left(x+2\right)^{2011}=C_{2013}^12^{2012}+2^2C_{2013}^2x.2^{2011}+...+2013^2C_{2013}^{2013}x^{2012}\)
Thay \(x=1\)
\(\Rightarrow2013.3^{2012}+2012.2013.3^{2011}=1^2C_{2013}^12^{2012}+2^2C_{2013}^22^{2011}+...+2013^2C_{2013}^{2013}\)
\(\Rightarrow S=2013.3^{2012}+2012.2013.3^{2011}=2013.3^{2011}\left(3+2012\right)=2013.2015.3^{2011}\)
Đúng 0
Bình luận (0)
11.
Ta có:
\(\dfrac{1}{k+1}C_n^k=\dfrac{1}{k+1}.\dfrac{n!}{k!\left(n-k\right)!}=\dfrac{n!}{\left(k+1\right)!\left(n-k\right)!}=\dfrac{1}{n+1}.\dfrac{\left(n+1\right)!}{\left(k+1\right)!\left[\left(n+1\right)-\left(k+1\right)\right]!}\)
\(=\dfrac{1}{n+1}C_{n+1}^{k+1}\)
Do đó:
\(S=\dfrac{1}{2}.C_{2n}^1+\dfrac{2}{4}C_{2n}^3+...+\dfrac{1}{2n}C_{2n}^{2n-1}\)
\(=\dfrac{1}{2n+1}C_{2n+1}^2+\dfrac{1}{2n+1}C_{2n+1}^4+...+\dfrac{1}{2n+1}C_{2n+1}^{2n}\)
\(=\dfrac{1}{2n+1}\left(C_{2n+1}^2+C_{2n+1}^4+...+C_{2n+1}^{2n}\right)\)
Xét khai triển:
\(\left(1+x\right)^{2n+1}=C_{2n+1}^0+C_{2n+1}^1x+C_{2n+1}^2x^2+...+C_{2n+1}^{2n+1}x^{2n+1}\) (1)
Thay \(x=1\) vào (1):
\(\Rightarrow2^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+C_{2n+1}^2+...+C_{2n+1}^{2n+1}\) (2)
Thay \(x=-1\) vào (1):
\(0=C_{2n+1}^0-C_{2n+1}^1x+C_{2n+1}^2-....+C_{2n+1}^{2n}-C_{2n+1}^{2n+1}\) (3)
Cộng vế (2) và (3):
\(2^{2n+1}=2C_{2n+1}^0+2C_{2n+1}^2+...+2C_{2n+1}^{2n}\)
\(\Rightarrow C_{2n+1}^0+C_{2n+1}^2+C_{2n+1}^4+...+C_{2n+1}^{2n}=2^{2n}\)
\(\Rightarrow C_{2n+1}^2+C_{2n+1}^4+...+C_{2n+1}^{2n}=2^{2n}-C_{2n+1}^0=2^{2n}-1\)
\(\Rightarrow S=\dfrac{1}{2n+1}\left(2^{2n}-1\right)=\dfrac{2^{2n}-1}{2n+1}\)
Đúng 0
Bình luận (0)
Câu7,8,9 ạ
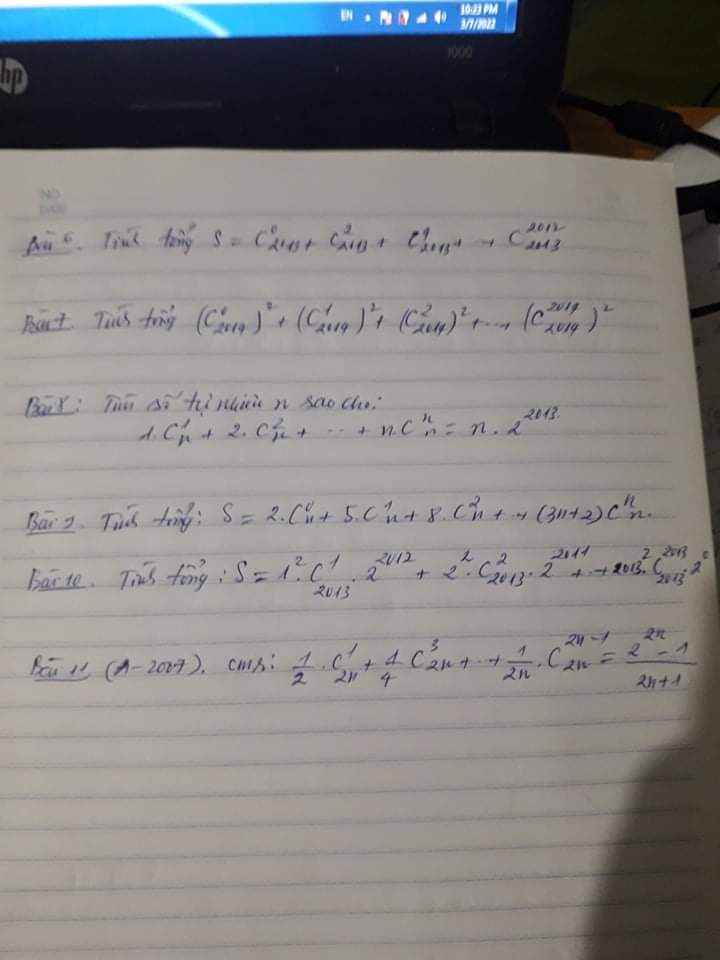
7.
Bài toán: từ 1 nhóm có 2n người, bao gồm đúng n nam và n nữa, hỏi có bao nhiêu cách chọn ra n người khác nhau.
- Cách chọn thứ nhất: chọn n người từ 2n người, có \(C_{2n}^n\) cách
- Cách chọn thứ 2: giả sử trong n người được chọn, có k nam và n-k nữ (với k từ 0 tới n)
Chọn k nam từ n nam: có \(C_n^k\) cách, chọn n-k nữ từ n nữ, có \(C_n^{n-k}=C_n^k\) cách
\(\Rightarrow\) có \(\sum\limits^n_{k=0}C_n^k.C_n^k=\sum\limits^n_{k=0}\left(C_n^k\right)^2\)
Do 2 cách chọn đều có kết quả giống nhau, suy ra:
\(C_{2n}^n=\sum\limits^n_{k=0}\left(C_n^k\right)^2=\left(C_n^0\right)^2+\left(C_n^1\right)^2+...+\left(C_n^n\right)^2\)
Thay \(n=2014\Rightarrow\left(C_{2014}^0\right)^2+\left(C_{2014}^1\right)^2+...+\left(C_{2014}^{2014}\right)^2=C_{4028}^{2014}\)
Đúng 0
Bình luận (0)
8.
Xét khai triển:
\(\left(1+x\right)^n=C_n^0+C_n^1x+C_n^2x^2+...+C_n^nx^n\)
Đạo hàm 2 vế:
\(n\left(1+x\right)^{n-1}=C_n^1+2C_n^2x+...+nC_n^nx^{n-1}\)
Thay \(x=1\) vào đẳng thức trên ta được:
\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^n\)
\(\Rightarrow n.2^{n-1}=n.2^{2013}\)
\(\Rightarrow n-1=2013\)
\(\Rightarrow n=2014\)
Đúng 0
Bình luận (0)
Câu 8 nếu ko sử dụng đạo hàm thì còn cách khác như sau:
Ta có:
\(kC_n^k=k.\dfrac{n!}{k!\left(n-k\right)!}=\dfrac{n!}{\left(k-1\right)!\left(n-k!\right)}=n.\dfrac{\left(n-1\right)!}{\left(k-1\right)!\left[\left(n-1\right)-\left(k-1\right)\right]!}=n.C_{n-1}^{k-1}\)
Từ đó ta có:
\(1.C_n^1+2C_n^2+3C_n^3+...+nC_n^n=nC_{n-1}^0+nC_{n-1}^1+...+nC_{n-1}^{n-1}\)
\(=n\left(C_{n-1}^0+C_{n-1}^1+...+C_{n-1}^{n-1}\right)\)
\(=n.2^{n-1}\)
\(\Rightarrow n.2^{n-1}=n.2^{2013}\Rightarrow n=2014\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Câu 5 ạ
Xét khai triển:
\(\left(1+x\right)^{2013}=C_{2013}^0+C_{2013}^1.x+C_{2013}^2x^2+...+C_{2013}^{2013}x^{2013}\)
Thay \(x=3\) ta được:
\(4^{2013}=C_{2013}^0+3C_{2013}^1+3^2C_{2013}^2+...+3^{2013}C_{2013}^{2013}\)
Vậy \(S=4^{2013}\)
Đúng 2
Bình luận (0)
Tìm hệ số của x13 trong khai triển \(f\left(x\right)=\left(\dfrac{1}{4}+x+x^2\right)^3\left(2x+1\right)^{15}\) thành đa thức
\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....
Đúng 1
Bình luận (0)




