Tìm số hạng chứa x6 trong khai triển (2x - 1/3)13
Giúp em giải câu nàu được không vậy ạ. Có thể cho em xin câu trả lời chi tiết được không vậy
Tìm số hạng chứa x6 trong khai triển (2x - 1/3)13
Giúp em giải câu nàu được không vậy ạ. Có thể cho em xin câu trả lời chi tiết được không vậy
Số hạng tổng quát là:
\(C^k_{13}\cdot\left(2x\right)^{13-k}\cdot\left(-\dfrac{1}{3}\right)^k\)
Số hạng chứa x^6 sẽ tươg ứng với 13-k=6
=>k=7
=>Số hạng cần tìm là \(C^7_{13}\cdot\left(2x\right)^6\cdot\left(-\dfrac{1}{3}\right)^7\)
Tìm số hạng thứ 15 trong khai triển (2x - 3y)17
Ai có thể giúp mình giải bài này được không ạ. Nếu được có thể giải chi tiết mình xin cảm ơn rất nhiều.
Số hạng tổng quát là \(C^k_{17}\cdot\left(2x\right)^{17-k}\cdot\left(-3y\right)^k\)
Số hạng thứ 15 sẽ tương ứng với k=14
=>Số hạng thứ 15 là \(C^{14}_{17}\cdot\left(2k\right)^3\cdot\left(-3y\right)^{14}\)
Tìm hệ số của số hạng chứa x8 trong khai triển \(\left[1+x^2\left(1-x\right)\right]^{8^{ }}\)
\(\left[1+x^2\left(1-x\right)\right]^8\)
\(=\left(1+x^2-x^3\right)^8\)
\(=\sum_{k=1}^8C_8^k\left(x^2-x^3\right)^k.1^{\left(8-k\right)}\) ($k \leq 8$)
\(=\sum_{k=1}^8C_8^k\sum_{i=1}^kC^i_kx^{2i}.x^{3k-3i}\left(-1\right)^{k-i}\) ($i \leq k$)
\(=\sum_{k=1}^8C_8^k\sum_{i=1}^kC^i_kx^{3k-i}.\left(-1\right)^{k-i}\)
\(=\sum_{k=1}^8\sum_{i=1}^kC_8^kC^i_k\left(-1\right)^{k-i}x^{3k-i}\)
Hệ số của $x^{3k-i}$ là \(C_8^kC^i_k\left(-1\right)^{k-i}\).
Tìm $k;i$ thoả mãn $i \leq k \leq 8$, và $3k-i=8$.
| $k$ | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| $i$ | 16 | 13 | 10 | 7 | 4 | 1 | -2 | -5 |
Vậy hệ số của $x^8$ $=$ \(C_8^4C^4_4\left(-1\right)^{4-4}+C_8^3C^1_3\left(-1\right)^{3-1}\) $=238$.
Tìm hệ số không chứa x trong khai triển \(\left(2x^2-\dfrac{1}{x}\right)^8\) với x khác 0
Lời giải:
Theo nhị thức Newton:
\((2x^2-\frac{1}{x})^8=\sum \limits_{k=0}^8C^k_8(2x^2)^k(x^{-1})^{8-k}=\sum \limits_{k=0}^8C^k_82^kx^{3k-8}\)
Hệ số không chứa $x$ là $C^k_8.2^k$ sao cho $3k-8=0\Leftrightarrow k=\frac{8}{3}$ (loại vì $k$ nguyên)
Vậy hệ số tự do (hệ số không chứa x trong khai triển) là $0$
Biết hệ số của x2 trong khai triển của \(\left(1+4x\right)^n\) là 3040. Tìm n
Tìm hệ số của x^7 trong khai triển nhị thức Newton của ( x^2-2/x)n biết rằng n là số nguyên dương thỏa mãn a3n -2c2n =4c3 n+1 (Toán học - Lớp 11)
\(A^3_n-2\cdot C^2_n=4C^3_{n+1}\)(ĐK: n>=3)
=>\(\dfrac{n!}{\left(n-3\right)!}-2\cdot\dfrac{n!}{\left(n-2\right)!\cdot1}=4\cdot\dfrac{\left(n+1\right)!}{\left(n-2\right)!\cdot3!}\)
=>\(n\left(n-1\right)\left(n-2\right)-n\left(n-1\right)=4\cdot\dfrac{\left(n-1\right)\cdot n\cdot\left(n+1\right)}{6}\)
=>n(n-1)(n-3)=2/3(n-1)*n*(n+1)
=>n(n-1)(n-3-2/3n-2/3)=0
=>1/3n-11/3=0
=>n=11
=>(x^2-2/x)^11
SHTQ là: \(C^k_{11}\cdot\left(x^2\right)^{11-k}\cdot\left(-\dfrac{2}{x}\right)^k=C^k_{11}\cdot\left(-2\right)^k\cdot x^{22-3k}\)
SHTƯ với x^7 sẽ tương ứng vơi 22-3k=7
=>k=5
=>Hệ số là \(C^5_{11}\cdot\left(-2\right)^5\)
Bài 1. Viết khai triển tổng quát theo công thức nhị thức Newton:
a) \(\left(a+2b\right)^5\)
b) \(\left(a-\sqrt{2}\right)^6\)
c) \(\left(x-\dfrac{1}{x}\right)^{13}\)
Khai triển nhị sau A) (3+2x^3)^6 B) (2x+3x^2)^7
a: (2x^3+3)^6
\(=C^0_6\cdot\left(2x^3\right)^6\cdot3^0+C^1_6\cdot\left(2x^3\right)^5\cdot3^1+...+C^6_6\cdot3^6\)
=
 b: (3x^2+2x)^7
b: (3x^2+2x)^7
\(=C^0_7\cdot\left(3x^2\right)^7+C^1_7\cdot\left(3x^2\right)^6\cdot2x+...+C^7_7\cdot\left(2x\right)^7\)
=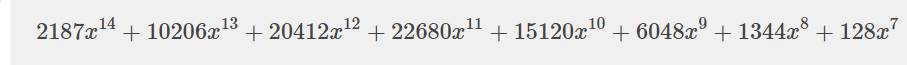
Khai triển nhị thức (1-x/2)^4
`(1-x/2)^4=C^0 _4.1^4-C^1 _4 .1^3 . x/2+C^2 _4 . 1^2 .(x/2)^2-C^3 _4 .1^1 .(x/2)^3+C^4 _4 (x/2)^4`
`=1-2x+3/2x^2-1/2x^3+1/16 x^4`
Khai triển các nhị thức sau A) (2x-+3y)^5 B)(1-2/x)^6
a: \(=C^0_5\cdot\left(2x\right)^5+C^1_5\cdot\left(2x\right)^4\cdot\left(3y\right)^1+C^2_5\cdot\left(2x\right)^3\cdot\left(3y\right)^2+C^3_5\cdot\left(2x\right)^2\cdot\left(3y\right)^3+C^4_5\cdot2x\cdot\left(3y\right)^4+C^5_5\cdot\left(3y\right)^5\)
\(=32x^5+240x^4y+720x^3y^2+1080x^2y^3+810xy^4+243y^5\)
b: \(=C^0_6\cdot1^6\cdot\left(-\dfrac{2}{x}\right)^0+C^1_6\cdot\left(-\dfrac{2}{x}\right)^1+C^2_6\cdot\left(-\dfrac{2}{x}\right)^2+C^3_6\cdot\left(-\dfrac{2}{x}\right)^3+C^4_6\cdot\left(-\dfrac{2}{x}\right)^4+C^5_6\cdot\left(-\dfrac{2}{x}\right)^5+C^6_6\cdot\left(-\dfrac{2}{x}\right)^6\)
\(=1-\dfrac{12}{x}+\dfrac{60}{x^2}-\dfrac{160}{x^3}+\dfrac{240}{x^4}-\dfrac{192}{x^5}+\dfrac{64}{x^6}\)