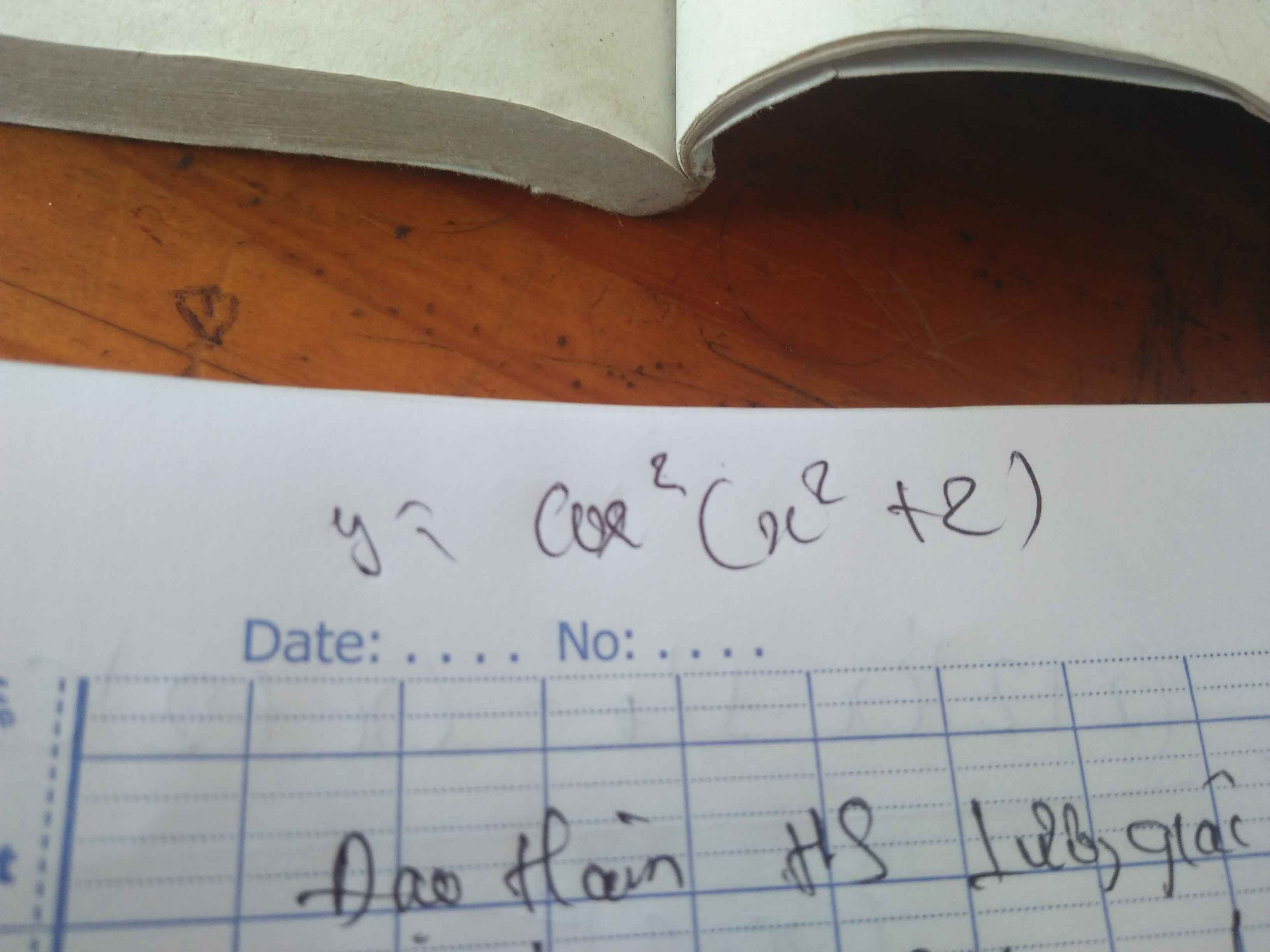Bài 3: Đạo hàm của hàm số lượng giác
Bài 8:
Ta có: \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{2x^2-x-6}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2+2x+4}{2x+3}=\dfrac{12}{7}\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(mx+10\right)=2m+10\)
\(f\left(2\right)=2m+10\)
Để f(x) liên tục tại x0 = 2 thì \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)\)
\(\Rightarrow2m+10=\dfrac{12}{7}\Rightarrow m=\dfrac{-29}{7}\)
Vậy...
Bài 9:
Ta có: \(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+x}-\sqrt{1-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{1+x-\left(1-x\right)}{x\left(\sqrt{1+x}+\sqrt{1-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{1+x}+\sqrt{1-x}}=1\)
\(f\left(0\right)=-5m+2\)
Để f(x) liên tục tại x0 = 0 thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow-5m+2=1\Rightarrow m=\dfrac{1}{5}\)
Vậy...
Câu 10:
Ta có:
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{2x-1}-1}{x^2+2x-3}=\lim\limits_{x\rightarrow1^+}\dfrac{2x-1-1}{\left(x-1\right)\left(x+3\right)\left(\sqrt{2x-1}+1\right)}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{2}{\left(x+3\right)\left(\sqrt{2x-1}+1\right)}=\dfrac{1}{4}\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(x+m\right)=m+1\)
\(f\left(1\right)=m+1\)
Để f(x) liên tục tại x0 = 1 thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow m+1=\dfrac{1}{4}\Rightarrow m=\dfrac{-3}{4}\)
Vậy...
Đúng 0
Bình luận (0)
Bài 11:
Ta có: \(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{6+x}-2}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{6+x-8}{\left(x-2\right)\left(\sqrt[3]{\left(6+x\right)^2}+2\sqrt[3]{6+x}+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt[3]{\left(6+x\right)^2}+2\sqrt[3]{6+x}+4}=\dfrac{1}{12}\)
\(f\left(2\right)=4-m\)
Để f(x) liên tục tại x0 = 2 thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
\(\Rightarrow4-m=\dfrac{1}{12}\Rightarrow m=\dfrac{47}{12}\)
Vậy...
Bài 12:
Ta có: \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{12x-4}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{12x-4-8}{\left(x-1\right)\left(\sqrt[3]{\left(12x-4\right)^2}+2\sqrt[3]{12x-4}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{12}{\sqrt[3]{\left(12x-4\right)^2}+2\sqrt[3]{12x-4}+4}=1\)
\(f\left(1\right)=\sqrt{m^2+8}+2m\)
Để f(x) liên tục thì \(\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow\sqrt{m^2+8}+2m=1\)
\(\Leftrightarrow\sqrt{m^2+8}=1-2m\)
\(\Rightarrow m^2+8=1-4m+4m^2\) (ĐK: \(1-2m\ge0\Rightarrow m\le\dfrac{1}{2}\))
\(\Leftrightarrow3m^2-4m-7=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{7}{3}\left(ktm\right)\\m=-1\left(tm\right)\end{matrix}\right.\)
Vậy...
Đúng 0
Bình luận (0)
\(y'=2cos\left(x^2+2\right).\left[cos\left(x^2+2\right)\right]'=-4xcos\left(x^2+2\right).sin\left(x^2+2\right)\)
\(=-4x.sin\left(2x^2+4\right)\)
Đúng 1
Bình luận (0)
Cho hàm số y = (x^2+3x+3)/(x^2+1). Gỉai phương trình y'=0
\(y=\dfrac{x^2+3x+3}{x^2+1}\Rightarrow y'=\dfrac{\left(x^2+3x+3\right)'\left(x^2+1\right)-\left(x^2+3x+3\right)\left(x^2+1\right)'}{\left(x^2+1\right)^2}\)
\(y'=\dfrac{\left(x^2+1\right)\left(2x+3\right)-\left(x^2+3x+3\right).2x}{\left(x^2+1\right)^2}\)
\(y'=0\Leftrightarrow\left(x^2+1\right)\left(2x+3\right)-2x\left(x^2+3x+3\right)=0\)
\(\Leftrightarrow2x^3+3x^2+2x+3-2x^3-6x^2-6x=0\)
\(\Leftrightarrow3x^2+4x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=..\\x=...\end{matrix}\right.\)
Check lai ho t nhe
Đúng 2
Bình luận (0)
cho I = Limx→0 2(√3x+1 -1)/x và J = limx→-1 x2-x-2 / x+ 1. tính I-J
X
\(\lim\limits_{x\rightarrow0}\dfrac{2\left(\sqrt{3x+1}-1\right)}{x}=\lim\limits_{x\rightarrow0}\dfrac{6x}{x\left(\sqrt{3x+1}+1\right)}=\lim\limits_{x\rightarrow0}\dfrac{6}{\sqrt{3x+1}+1}=3\)
\(\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x-2\right)}{x+1}=\lim\limits_{x\rightarrow-1}\left(x-2\right)=-3\)
\(\Rightarrow I-J=6\)
Đúng 0
Bình luận (0)
Tìm đạo hàm y' với y=\(\sqrt{X+\sqrt{1+x^2}}\). Mong mn giải chi tiết xíu để em có thể hiểu rõ hơn ạ
Lời giải:
Em không rõ ở phần tìm đạo hàm theo định nghĩa (lim) hay tìm đạo hàm dựa theo công thức
Thông thường lớp 11 thì thường áp dụng luôn công thức
Áp dụng công thức: \((u^{\alpha})'=\alpha.u'.u^{\alpha-1}\) thì:
\(y=(x+\sqrt{1+x^2})^{\frac{1}{2}}\)
\(\Rightarrow y'=\frac{1}{2}(x+\sqrt{x^2+1})'(x+\sqrt{x^2+1})^{\frac{1}{2}-1}\)
\(=\frac{(x+\sqrt{x^2+1})'}{2\sqrt{x+\sqrt{x^2+1}}}(*)\)
\((x+\sqrt{x^2+1})'=x'+(\sqrt{x^2+1})'=1+((x^2+1)^{\frac{1}{2}})'\)
\(=1+\frac{1}{2}(x^2+1)'(x^2+1)^{\frac{1}{2}-1}\)
\(=1+\frac{1}{2}.2x.\frac{1}{\sqrt{x^2+1}}=1+\frac{x}{\sqrt{x^2+1}}(**)\)
Từ \((*);(**)\Rightarrow y'=\frac{x+\sqrt{x^2+1}}{\sqrt{x^2+1}.2\sqrt{x+\sqrt{x^2+1}}}=\frac{1}{2}\sqrt{\frac{x+\sqrt{x^2+1}}{x^2+1}}\)
Đúng 0
Bình luận (0)
ta có : \(y'=\left(\sqrt{x+\sqrt{1+x^2}}\right)'=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(x+\sqrt{1+x^2}\right)'\)
\(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(1+\dfrac{1}{2\sqrt{1+x^2}}\left(1+x^2\right)'\right)\) \(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(1+\dfrac{2x}{2\sqrt{1+x^2}}\right)\) \(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}\right)=\dfrac{1}{2}\sqrt{\dfrac{x+\sqrt{1+x^2}}{1+x^2}}\)
Đúng 0
Bình luận (0)
Tìm đạo hàm
y = cot2x + cot2x
Lời giải:
\(y=\cot ^2x+\cot 2x\)
\(\Rightarrow y'=(\cot ^2x)'+(\cot 2x)'\)
\(=2(\cot x)'\cot x+\frac{-(2x)'}{\sin ^22x}\)
\(=2.\frac{-1}{\sin ^2x}\cot x-\frac{2}{\sin ^22x}\)
\(=-2(\frac{\cot x}{\sin ^2x}+\frac{1}{\sin ^22x})\)
Đúng 0
Bình luận (0)
đạo hàm của hàm số sau y=cos3x * sin2x
\(y'=\left(cos3x\times sin2x\right)'\)
\(\left(cos3x\right)'sin2x+cos3x\left(sin2x\right)'\)
\(-\left(3x\right)'sin3x\sin2x+\left(2x\right)'\cos2x\cos3x\)
\(-3\sin3x\sin2x+2\cos2x\cos3x\)
\(\dfrac{-3}{2}\left[\cos x-\cos5x\right]+\left[\cos x+\cos5x\right]\)
\(\dfrac{5}{2}\cos5x-\dfrac{1}{2}\cos x\)
Đúng 0
Bình luận (0)
Cho hàm số f(x)=\(sin^2\left(\dfrac{\pi}{6}-x\right)+sin^2\left(\dfrac{\pi}{6}+x\right)\) . Chứng minh rằng f '(x)=sin2x
Lời giải:
Ta có:
\(f(x)=\sin ^2\left(\frac{\pi}{6}-x\right)+\sin ^2\left(\frac{\pi}{6}+x\right)\)
\(\Rightarrow f'(x)=2\sin \left(\frac{\pi}{6}-x\right).-\cos \left(\frac{\pi}{6}-x\right)+2\sin \left(\frac{\pi}{6}+x\right)\cos \left(\frac{\pi}{6}+x\right)\)
\(f'(x)=-\sin 2\left(\frac{\pi}{6}-x\right)+\sin 2\left(\frac{\pi}{6}+x\right)\)
Áp dụng công thức: \(\sin a-\sin b=2\cos \frac{a+b}{2}\sin \frac{a-b}{2}\) suy ra:
\(f'(x)=-\sin \left(\frac{\pi}{3}-2x\right)+\sin \left(\frac{\pi}{3}+2x\right)\)
\(f'(x)=2\cos \left(\frac{\pi}{3}\right)\sin 2x=\sin 2x\) (đpcm)
Đúng 0
Bình luận (1)
Đạo hàm cấp 2017 của hàm số y=sin x là
A.sin x B.-sin x C.cos x D.-cos x