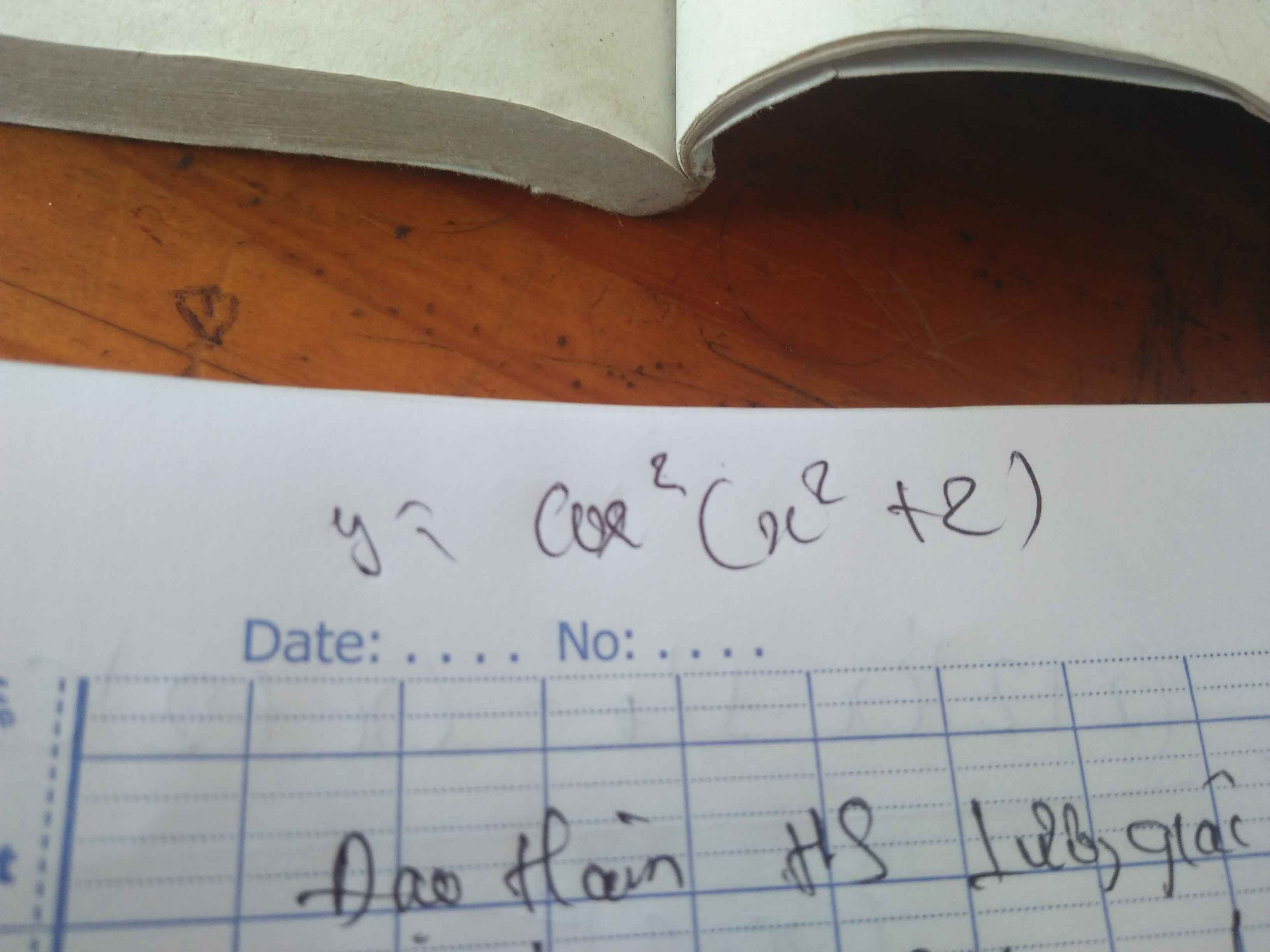Bài 8:
Ta có: \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{2x^2-x-6}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2+2x+4}{2x+3}=\dfrac{12}{7}\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(mx+10\right)=2m+10\)
\(f\left(2\right)=2m+10\)
Để f(x) liên tục tại x0 = 2 thì \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)\)
\(\Rightarrow2m+10=\dfrac{12}{7}\Rightarrow m=\dfrac{-29}{7}\)
Vậy...
Bài 9:
Ta có: \(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+x}-\sqrt{1-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{1+x-\left(1-x\right)}{x\left(\sqrt{1+x}+\sqrt{1-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{1+x}+\sqrt{1-x}}=1\)
\(f\left(0\right)=-5m+2\)
Để f(x) liên tục tại x0 = 0 thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow-5m+2=1\Rightarrow m=\dfrac{1}{5}\)
Vậy...
Câu 10:
Ta có:
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{2x-1}-1}{x^2+2x-3}=\lim\limits_{x\rightarrow1^+}\dfrac{2x-1-1}{\left(x-1\right)\left(x+3\right)\left(\sqrt{2x-1}+1\right)}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{2}{\left(x+3\right)\left(\sqrt{2x-1}+1\right)}=\dfrac{1}{4}\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(x+m\right)=m+1\)
\(f\left(1\right)=m+1\)
Để f(x) liên tục tại x0 = 1 thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow m+1=\dfrac{1}{4}\Rightarrow m=\dfrac{-3}{4}\)
Vậy...
Bài 11:
Ta có: \(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{6+x}-2}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{6+x-8}{\left(x-2\right)\left(\sqrt[3]{\left(6+x\right)^2}+2\sqrt[3]{6+x}+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt[3]{\left(6+x\right)^2}+2\sqrt[3]{6+x}+4}=\dfrac{1}{12}\)
\(f\left(2\right)=4-m\)
Để f(x) liên tục tại x0 = 2 thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
\(\Rightarrow4-m=\dfrac{1}{12}\Rightarrow m=\dfrac{47}{12}\)
Vậy...
Bài 12:
Ta có: \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{12x-4}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{12x-4-8}{\left(x-1\right)\left(\sqrt[3]{\left(12x-4\right)^2}+2\sqrt[3]{12x-4}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{12}{\sqrt[3]{\left(12x-4\right)^2}+2\sqrt[3]{12x-4}+4}=1\)
\(f\left(1\right)=\sqrt{m^2+8}+2m\)
Để f(x) liên tục thì \(\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\)
\(\Rightarrow\sqrt{m^2+8}+2m=1\)
\(\Leftrightarrow\sqrt{m^2+8}=1-2m\)
\(\Rightarrow m^2+8=1-4m+4m^2\) (ĐK: \(1-2m\ge0\Rightarrow m\le\dfrac{1}{2}\))
\(\Leftrightarrow3m^2-4m-7=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{7}{3}\left(ktm\right)\\m=-1\left(tm\right)\end{matrix}\right.\)
Vậy...