Bài 2: Hàm số bậc nhất.

Vì |a+b| \(\ge\)0, |a-b|\(\ge\)0, nên |a+b|>|a-b|

\(\Leftrightarrow\)a²+2ab+b² \(\ge\)a²-2ab+b²

\(\Leftrightarrow\)4ab>0

\(\Leftrightarrow\)ab>0

Vậy a và b là hai số cùng dấu.

a: Thay x=-1 và y=1 vào (d), ta được:

-(a-1)+a=1

=>-a+1+a=1

=>1=1(luôn đúng)

b: Thay x=0 và y=3 vào (d), ta được;

0(a-1)+a=3

=>a=3

=>y=2x+3

c: Thay x=-2 và y=0 vào (d), ta được;

-2(a-1)+a=0

=>-2a+2+a=0

=>2-a=0

=>a=2

a, Để hàm số là hàm bậc nhất thì \(\left(-m^2+m-2\right)\ne0\)

\(\Rightarrow-\left(m-\dfrac{1}{2}\right)^2-\dfrac{7}{4}\ne0\) (luôn đúng vì \(-\left(m-\dfrac{1}{2}\right)^2\le0\forall m\))

Vậy hàm số luôn là hàm bậc nhất.

b,Để hàm số là hàm bậc nhất thì \(\left\{{}\begin{matrix}2m^2-6m=0\\2m+3\ne0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}m=0\\m=3\\m\ne-\dfrac{3}{2}\end{matrix}\right.\left(tm\right)\)

Vậy hàm số là hàm bậc nhất khi m ∈ {0;3}.

a: y=m^2x-4mx+8m+4x+3

=x(m^2-4m+4)+8m+3

Để đây là hàm số bậc nhất thì m^2-4m+4<>0

=>(m-2)^2<>0

=>m-2<>0

=>m<>2

b: Để đây là hàm số bậc nhất thì \(\left\{{}\begin{matrix}2018-2m>=0\\\sqrt{2018-2m}< >0\end{matrix}\right.\Leftrightarrow2018-2m>0\)

=>2m<2018

=>m<1009

`a)` Hàm số xác định `<=>{(5x+3 >= 0),(2x+1 >= 0):}`

                                 `<=>{(x >= -3/5),(x >= -1/2):}<=>x >= -1/2`

`b)` Hàm số xác định `<=>{(x-7 >= 0),(14-x >= 0):}`

                    `<=>{(x >= 7),(x <= 14):}<=>7 <= x <= 14`

y=3/2x có a=3/2>0

=>y=3/2x đồng biến

y=-4x có a=-4<0

=>y=-4x nghịch biến

a: 

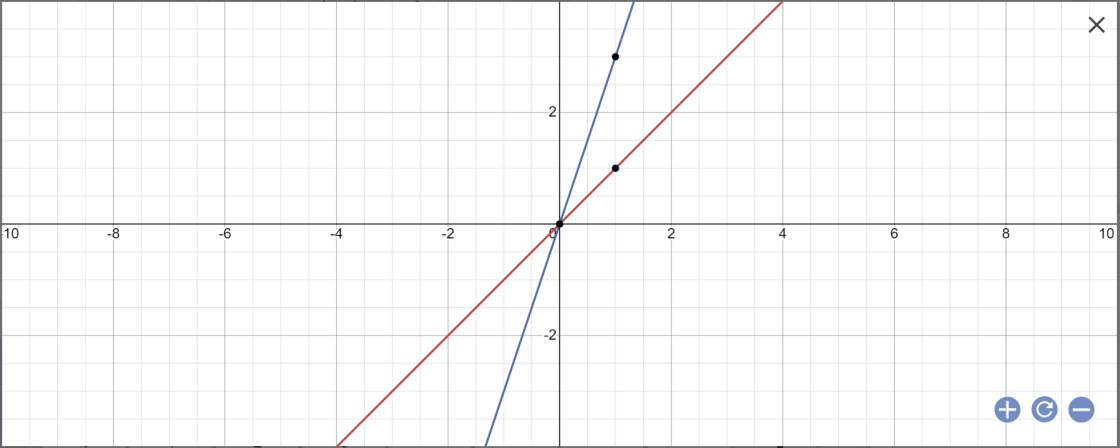
b: Tọa độ A là:

x=y và y=6

=>x=y=6

=>A(6;6)

Tọa độ B là;

y=3x và y=6

=>3x=6 và y=6

=>x=2 và y=6

=>B(2;6)

a: Để hàm số đồng biến thì -3/(4m-5)>0

=>4m-5<0

=>m<5/4

b: Để hàm số nghịch biến thì -3/(4m-5)<0

=>4m-5>0

=>m>5/4

 Cho mình hỏi : A = ( x thuộc N / 2x + 2 ; x bé hơn 100 mình cần gấp lắm rồi,

8:

a: Để đây là hsbn thì m-1<>0

=>m<>1

b: Để hàm số đồng biến thì m-1>0

=>m>1

Để hàm số nghịch biến thì m-1<0

=>m<1

c: Thay x=3 và y=4 vào (d) ta được:

3(m-1)+5=4

=>3m+2=4

=>3m=2

=>m=2/3

\(\Delta=\left(1\right)^2-4.1.2m=1-8m\) 

phương trình có nghiệm \(\Delta\ge0\\ \Leftrightarrow1-8m\ge0\\ \Leftrightarrow m\le\dfrac{1}{8}\)

Vậy với \(m\le\dfrac{1}{8}\) thì pt có nghiệm