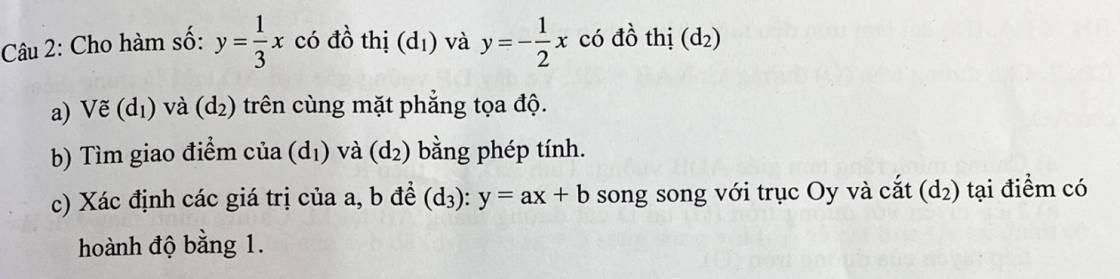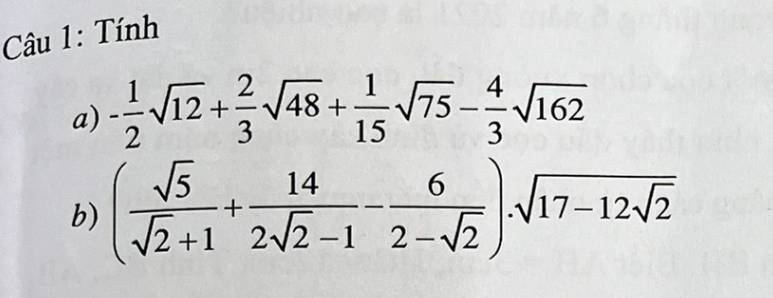Bài 2: Căn thức bậc hai và hằng đẳng thức căn bậc hai của bình phương
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó;ΔADB vuông tại D
Xét ΔDAO có
DI là đường cao
DI là đường trung tuyến
Do đó: ΔDAO cân tại D
Xét ΔDAO cân tại D có OA=OD(=R)
nên ΔDAO đều
=>DA=R và \(\widehat{DAO}=60^0\)
Ta có: ΔDAB vuông tại D
=>\(DA^2+DB^2=AB^2\)
=>\(DB^2=\left(2R\right)^2-R^2=3R^2\)
=>\(DB=R\sqrt{3}\)
b: Ta có: ΔOED cân tại O
mà OI là đường cao
nên I là trung điểm của ED và OI là phân giác của góc DOE
Xét ΔODM và ΔOEM có
OD=OE
\(\widehat{DOM}=\widehat{EOM}\)
OM chung
Do đó: ΔODM=ΔOEM
=>\(\widehat{ODM}=\widehat{OEM}=90^0\)
=>ME là tiếp tuyến của (O)
c: Xét (O) có
\(\widehat{MDA}\) là góc tạo bởi tiếp tuyến DM và dây cung DA
\(\widehat{ABD}\) là góc nội tiếp chắn cung DA
Do đó: \(\widehat{MDA}=\widehat{ABD}=\widehat{MBD}\)
Xét ΔMDA và ΔMBD có
\(\widehat{MDA}=\widehat{MBD}\)
\(\widehat{DMA}\) chung
Do đó: ΔMDA đồng dạng với ΔMBD
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MD}\)
=>\(MD^2=MA\cdot MB\left(1\right)\)
Xét ΔMDO vuông tại D có DI là đường cao
nên \(MI\cdot MO=MD^2\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MI\cdot MO\)
Đúng 1
Bình luận (0)
AC=AH+CH
=3+12
=15(cm)
Xét ΔABC vuông tại B có BH là đường cao
nên \(BH^2=HA\cdot HC\)
=>\(BH^2=12\cdot3=36\)
=>\(BH=\sqrt{36}=6\left(cm\right)\)
Ta có: ΔBHA vuông tại H
=>\(HB^2+HA^2=AB^2\)
=>\(AB^2=6^2+3^2=45\)
=>\(AB=\sqrt{45}\simeq6,7\left(cm\right)\)
Ta có: ΔBHC vuông tại H
=>\(BC^2=BH^2+HC^2\)
=>\(BC^2=6^2+12^2=180\)
=>\(CB=\sqrt{180}\simeq13,4\left(cm\right)\)
Đúng 1
Bình luận (0)
Số tiền phải trả cho 1kWh trong 50kWh đầu tiên là:
\(50\cdot1549=77450\left(đồng\right)\)
Số tiền phải trả cho 1kWh trong 50kWh tiếp theo từ 51 đến 100 là:
\(50\cdot1600=80000\left(đồng\right)\)
Số tiền phải trả cho 1kWh trong 100kWh tiếp theo từ 101 đến 200 là:
\(100\cdot1858=185800\left(đồng\right)\)
Số tiền phải trả cho 1kWh trong 100kWh tiếp theo từ 201 đến 300 là:
\(100\cdot2340=234000\left(đồng\right)\)
Số tiền phải trả cho 1kWh trong 100kWh tiếp theo từ 301 đến 400 là:
\(100\cdot2615=261500\left(đồng\right)\)
Số tiền phải trả cho 1kWh trong 150kWh còn lại là:
\(150\cdot2701=405150\left(đồng\right)\)
Tổng số tiền phải trả(tính luôn thuế VAT) là:
(77450+80000+185800+234000+261500+405150)*110%=1368290(đồng)
Đúng 1
Bình luận (0)
a: Thay x=2 và y=21400000 vào y=ax+b, ta được:
\(a\cdot2+b=21400000\left(1\right)\)
Thay x=4 và y=17000000 vào y=ax+b, ta được:
\(a\cdot4+b=17000000\)(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=21400000\\4a+b=17000000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2a=4400000\\2a+b=21400000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2200000\\b=21400000-2a=21400000-4400000=17000000\end{matrix}\right.\)
b: ta có: a=-2200000 và b=17000000
=>y=-2200000x+17000000
Khi x=0 thì \(y=-2200000\cdot0+17000000=17000000\)
=>Giá ban đầu của chiếc laptop là 17000000 đồng
Đúng 1
Bình luận (0)
a:
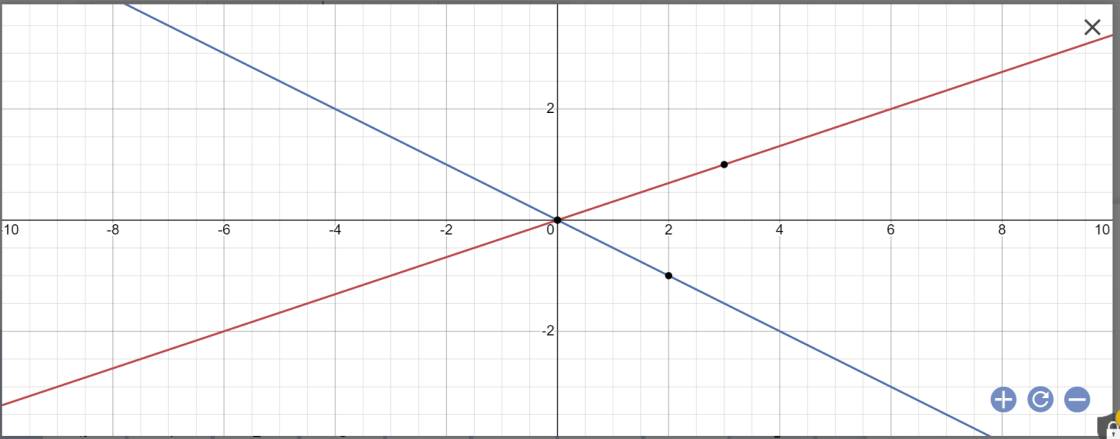
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{3}x=-\dfrac{1}{2}x\)
=>\(\dfrac{1}{3}x+\dfrac{1}{2}x=0\)
=>\(\dfrac{5}{6}x=0\)
=>x=0
Thay x=0 vào y=1/3x, ta được:
\(y=\dfrac{1}{3}\cdot0=0\)
c: Vì (d3)//Oy nên x=b+0y
Thay x=1 vào (d2), ta được:
\(y=-\dfrac{1}{2}\cdot1=-\dfrac{1}{2}\)
Thay x=1 và y=-1/2 vào (d3), ta được:
\(1=b+0\cdot\dfrac{-1}{2}\)
=>b=1
=>y=1
=>(d3): y=1
Đúng 1
Bình luận (0)
a: \(-\dfrac{1}{2}\sqrt{12}+\dfrac{2}{3}\cdot\sqrt{48}+\dfrac{1}{15}\cdot\sqrt{75}-\dfrac{4}{3}\cdot\sqrt{162}\)
\(=-\dfrac{1}{2}\cdot2\sqrt{3}+\dfrac{2}{3}\cdot4\sqrt{3}+\dfrac{1}{15}\cdot5\sqrt{3}-\dfrac{4}{3}\cdot9\sqrt{2}\)
\(=-\sqrt{3}+\dfrac{8}{3}\sqrt{3}+\dfrac{1}{3}\sqrt{3}-12\sqrt{2}\)
\(=2\sqrt{3}-12\sqrt{2}\)
b: \(\left(\dfrac{\sqrt{5}}{\sqrt{2}+1}+\dfrac{14}{2\sqrt{2}-1}-\dfrac{6}{2-\sqrt{2}}\right)\cdot\sqrt{17-12\sqrt{2}}\)
\(=\left(\dfrac{\sqrt{5}\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}+\dfrac{14\left(2\sqrt{2}+1\right)}{8-1}-\dfrac{6\left(2+\sqrt{2}\right)}{4-2}\right)\cdot\sqrt{\left(3-2\sqrt{2}\right)^2}\)
\(=\left(\sqrt{5}\left(\sqrt{2}-1\right)+2\left(2\sqrt{2}+1\right)-3\left(2+\sqrt{2}\right)\right)\cdot\left(3-2\sqrt{2}\right)\)
\(=\left(\sqrt{10}-\sqrt{5}+4\sqrt{2}+2-6-3\sqrt{2}\right)\left(3-2\sqrt{2}\right)\)
\(=\left(\sqrt{10}-\sqrt{5}+\sqrt{2}-4\right)\left(3-2\sqrt{2}\right)\)
\(=3\sqrt{10}-2\sqrt{20}-3\sqrt{5}+2\sqrt{10}+3\sqrt{2}-4-12+8\sqrt{2}\)
\(=5\sqrt{10}-4\sqrt{5}-3\sqrt{5}+11\sqrt{2}-16\)
\(=5\sqrt{10}-7\sqrt{5}+11\sqrt{2}-16\)
Đúng 1
Bình luận (0)
a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA và DM=DB
nên CA+DB=CD
b: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Ta có: ΔMAB vuông tại M
=>\(MA^2+MB^2=AB^2\)
=>\(MB^2=\left(2R\right)^2-R^2=3R^2\)
=>\(MB=R\sqrt{3}\)
Xét ΔMAB vuông tại A có MH là đường cao
nên \(MH\cdot AB=MA\cdot MB\)
=>\(MH\cdot2R=R\cdot R\sqrt{3}=R^2\sqrt{3}\)
=>\(MH=\dfrac{R^2\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{4,5^2+6^2}=7,5$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$BH.BC=AB^2\Rightarrow BH=\frac{AB^2}{BC}=\frac{4,5^2}{7,5}=2,7$ (cm)
$CH=BC-BH=7,5-2,7=4,8$ (cm)
$AH=AB.AC:BC=4,5.6:7,5=3,6$ (cm)
Đúng 2
Bình luận (0)