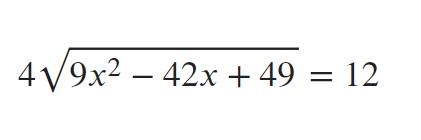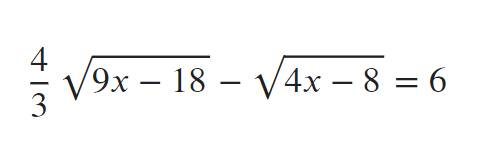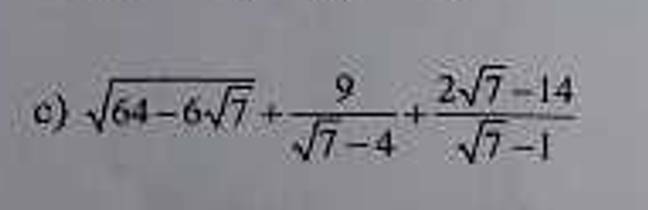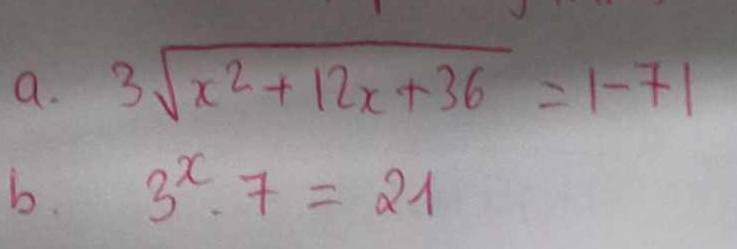
Bài 2: Căn thức bậc hai và hằng đẳng thức căn bậc hai của bình phương

Lời giải:
a.

$3\sqrt{x^2+12x+36}=|-7|$

$\Leftrightarrow 2\sqrt{(x+6)^2}=7$

$\Leftrightarrow 2|x+6|=7$

$\Leftrightarrow |x+6|=3,5$

$\Leftrightarrow x+6=3,5$ hoặc $x+6=-3,5$

$\Leftrightarrow x=-3,5$ hoặc $x=-9,5$ (đều tm)

b.

$3^x.7=21$

$3^x=21:7=3=3^1$

$\Rightarrow x=1$

\(4\sqrt{9x^2-42x+49}=12\\ \Leftrightarrow\sqrt{\left(3x-7\right)^2}=3\\ \Leftrightarrow\left|3x-7\right|=3\\ \Leftrightarrow\left[{}\begin{matrix}3x-7=3\\3x-7=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=10\\3x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{10}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)

Vậy \(S=\left\{\dfrac{10}{3};\dfrac{4}{3}\right\}.\)

ĐKXĐ: \(x\ge2\)

PT tương đương:

\(\dfrac{4}{3}.\sqrt{9}.\sqrt{x-2}-\sqrt{4}.\sqrt{x-2}=6\\ \Leftrightarrow\sqrt{x-2}.\left(4-2\right)=6\\ \Leftrightarrow x-2=9\\ \Leftrightarrow x=11\left(tm\right)\)

\(\dfrac{4}{3}\sqrt{9x-18}-\sqrt{4x-8}=6\\ \Leftrightarrow\dfrac{4}{3}\sqrt{9\left(x-2\right)}-\sqrt{4\left(x-2\right)}=6\\ \Leftrightarrow4\sqrt{x-2}-2\sqrt{x-2}=6\\ \Leftrightarrow2\sqrt{x-2}=6\\ \Leftrightarrow\sqrt{x-2}=3\\ \Leftrightarrow\left(\sqrt{x-2}\right)^2=3^2\\ \Leftrightarrow x-2=9\\ \Leftrightarrow x=11.\)

ĐKXĐ: \(x\ge2\)

\(\sqrt{9x-18}-\sqrt{4x-8}=6\\ \Leftrightarrow\sqrt{9}.\sqrt{x-2}-\sqrt{4}.\sqrt{x-2}=6\\ \Leftrightarrow\sqrt{x-2}.\left(3-2\right)=6\\ \Leftrightarrow x-2=36\Rightarrow x=38\left(tm\right)\)

a: Xét (O) có

ΔACD nội tiếp

AC là đường kính

Do đó: ΔACD vuông tại D

=>AD\(\perp\)DC tại D

=>AD\(\perp\)BC tại D

Xét ΔABC vuông tại A có AD là đường cao

nên \(AB^2=BD\cdot BC\)

b: Ta có: ΔDAB vuông tại D

mà DE là đường trung tuyến

nên DE=EA=EB=AB/2

Xét ΔOAE và ΔODE có

OA=OD

AE=DE

OE chung

Do đó: ΔOAE=ΔODE

=>\(\widehat{OAE}=\widehat{ODE}\)

mà \(\widehat{OAE}=90^0\)

nên \(\widehat{ODE}=90^0\)

=>ED là tiếp tuyến của (O)

c: Ta có: DK\(\perp\)AC

AB\(\perp\)AC

Do đó: DK//AB

Xét ΔCAE có KF//AE
nên \(\dfrac{KF}{AE}=\dfrac{CF}{CE}\left(1\right)\)

Xét ΔCEB có FD//EB

nên \(\dfrac{FD}{EB}=\dfrac{CF}{CE}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{KF}{AE}=\dfrac{FD}{EB}\)

mà AE=EB

nên KF=FD

=>F là trung điểm của KD

\(\sqrt{64-6\sqrt{7}}+\dfrac{9}{\sqrt{7}-4}+\dfrac{2\sqrt{7}-14}{\sqrt{7}-1}\\ =\sqrt{\left(3\sqrt{7}\right)^2-2\cdot3\sqrt{7}\cdot1+1^2}+\dfrac{9\left(\sqrt{7}+4\right)}{\left(\sqrt{7}-4\right)\left(\sqrt{7}+4\right)}+\dfrac{\left(2\sqrt{7}-14\right)\left(\sqrt{7}+1\right)}{\left(\sqrt{7}-1\right)\left(\sqrt{7}+1\right)}\\ =\sqrt{\left(3\sqrt{7}-1\right)^2}+\dfrac{9\left(\sqrt{7}+4\right)}{\sqrt{7}^2-4^2}+\dfrac{14+2\sqrt{7}-14\sqrt{7}-14}{\sqrt{7}^2-1^2}\\ =\left|3\sqrt{7}-1\right|-\sqrt{7}-4-\dfrac{12\sqrt{7}}{6}\\ =3\sqrt{7}-1-\sqrt{7}-4-2\sqrt{7}\\ =-5.\)

ĐKXĐ: x>=1

\(6+2\sqrt{\dfrac{x-1}{4}}=\sqrt{4x-4}+\dfrac{1}{3}\sqrt{9x-9}\)

=>\(6+2\cdot\dfrac{\sqrt{x-1}}{2}=2\sqrt{x-1}+\dfrac{1}{3}\cdot3\sqrt{x-1}\)

=>\(6+\sqrt{x-1}=2\sqrt{x-1}+\sqrt{x-1}\)

=>\(2\sqrt{x-1}=6\)

=>\(\sqrt{x-1}=3\)

=>x-1=9

=>x=10(nhận)

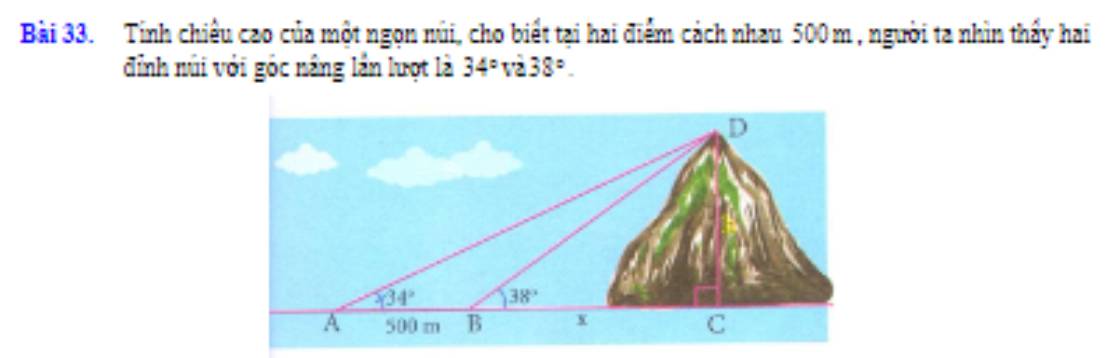
Ta có: \(\widehat{ABD}+\widehat{DBC}=180^0\)(hai góc kề bù)

=>\(\widehat{ABD}=180^0-38^0=142^0\)

Xét ΔABD có \(\widehat{ABD}+\widehat{ADB}+\widehat{DAB}=180^0\)

=>\(\widehat{ADB}+142^0+34^0=180^0\)

=>\(\widehat{ADB}=4^0\)

Xét ΔABD có \(\dfrac{AB}{sinADB}=\dfrac{AD}{sinABD}\)

=>\(\dfrac{500}{sin4}=\dfrac{AD}{sin142}\)

=>\(AD\simeq4412,93\left(m\right)\)

Xét ΔACD vuông tại C có \(sinA=\dfrac{DC}{DA}\)

=>\(DC=AD\cdot sinA\simeq2467,68\left(m\right)\)

Gọi số tiền ông Ba có lúc đầu là x (triệu đồng)

Điều kiện: x > 0. Khi đó:

Lợi tức ông Ba nhận được từ công ty rau sạch là: x/4.12%=0,03x (triệu đồng)

Lợi tức ông Ba nhận được từ hai công ty là 64 triệu đồng, nên ta có phương trình:

(chọn vì thỏa mãn điều kiện của ẩn)

Vậy số tiền ông Ba có lúc đầu là 800 triệu đồng