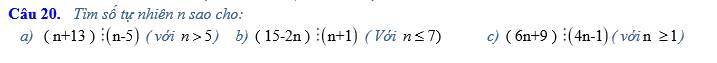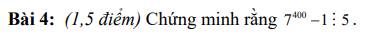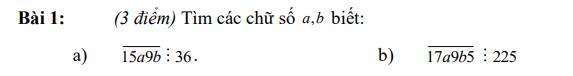Bài 11: Dấu hiệu chia hết cho 2, cho 5. Luyện tập
1. Đúng
2. Sai
3. Sai
4. Nhiều số lắm sẽ có nhiều kết quả
5. a.(-b)= b.(-a)
6. 98 x 97 = 9506
7. a. (-1) + a= (-a) + a = 0
9. Sai vì số 0 bình phương bằng 0
Đúng 2
Bình luận (0)
Bài 4: tìm các chữ số a, b để: b) số 5a43b chia hết cho cả 2; 5 và 9. c) số 735a2b chia hết cho5 &9 không chia hết cho 2. d) số 5a27b chia hết cho cả 2; 5 và 9 e) số 7a142b chia hết cho cả 2; 5 và 9. f) số 2a41b chia hết cho cả 2; 5 và 9. g) số 40ab chia hết cho cả 2; 3 và 5
Đọc tiếp
Bài 4: tìm các chữ số a, b để:
b) số 5a43b chia hết cho cả 2; 5 và 9.
c) số 735a2b chia hết cho5 &9 không chia hết cho 2.
d) số 5a27b chia hết cho cả 2; 5 và 9
e) số 7a142b chia hết cho cả 2; 5 và 9.
f) số 2a41b chia hết cho cả 2; 5 và 9.
g) số 40ab chia hết cho cả 2; 3 và 5
b: Đặt \(A=\overline{5a43b}\)
A chia hết cho 2 và 5 nên A có tận cùng là 0
=>b=0
=>\(A=\overline{5a430}\)
A chia hết cho 9
=>5+a+4+3+0 chia hết cho 9
=>a+12 chia hết cho 9
=>a=6
=>Số cần tìm là 56430
c: Đặt \(B=\overline{735a2b}\)
B chia hết cho 5 và không chia hết cho 2 nên b=5
=>\(B=\overline{735a25}\)
B chia hết cho 9
=>7+3+5+a+2+5 chia hết cho 9
=>a+22 chia hết cho 9
=>a=5
Vậy: Số cần tìm là 735525
d: Đặt \(C=\overline{5a27b}\)
C chia hết cho 2 và 5 nên C có tận cùng là 0
=>b=0
=>\(C=\overline{5a270}\)
C chia hết cho 9
=>5+a+2+7+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
Vậy: Số cần tìm là 54270
e: Đặt \(D=\overline{7a142b}\)
Vì D chia hết cho cả 2 và 5 nên D có tận cùng là 0
=>b=0
=>\(D=\overline{7a1420}\)
D chia hết cho 9
=>7+a+1+4+2+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
=>Số cần tìm là 741420
g: \(X=\overline{40ab}\)
X chia hết cho 2 và 5 nên b=0
=>\(X=\overline{40a0}\)
X chia hết cho 3
=>4+a+0+0 chia hết cho 3
=>a+4 chia hết cho 3
=>\(a\in\left\{2;5;8\right\}\)
Đúng 1
Bình luận (0)
xét Xem tổng nào chia hết cho 7 a 42+63+350
tất cả các tổng chia hết cho 7 vì: số 42;63;350 chia hết cho 7
Đúng 0
Bình luận (0)
Bài 1:Không thực hiện phép tính xét Xem biểu thức sau có chia hết cho 2 hay không vì sao
A = 1 + 2 + 3 + 4 +...+999
Bài 7 : Ko thực hiện phép tính, xét xem biểu thức sau có chia hết cho 5 hay ko? Vì sao ?
B = 1000 - 999 + 998 - 997 + ... + 4 - 3 + 2 - 1
Giải giúp mình vs ạ![]()
(Mình chỉ làm đc bài 1 thôi nhé)
Bài 1:
A = 1 + 2 + 3 + 4 +...+999
2A= (1+999)+(2+998)+(3+997)+...+(999+1)
Ta nhận thấy các kết quả của các tổng trong ngoặc trên đều bằng 1000 (số chẵn), mà các số chia hết cho 2 là số chẵn, suy ra A chia hết cho 2
Đúng 2
Bình luận (1)
hãy cho biết phép tính nào chia hết cho 2 phép tính nào chia hết cho 5
12368 , 37050,753465,90957
chia hết cho 2 : 12368 ,90957
chia hết cho 5 : 37050 ,753465
Đúng 1
Bình luận (0)
Gọi số đó là: \(a\) giả sử a chia cho 3 dư 0 hoặc 1 ta có 2 trường hợp:
Trường hợp 1:
\(a=3k\) (chia hết cho 3)
\(\Rightarrow a^2=\left(3k\right)^2=9k^2\) ⋮ 3 (luôn đúng) (2)
Trường hợp 2:
\(a=3k+1\) (chia cho 3 dư 1)
\(\Rightarrow a^2=\left(3k+1\right)^2=9k^2+6k+1=3k\left(3k+2\right)+1\) chia 3 dư 1 (đúng) (1)
Từ (1) và (2) kết luận số chính phương cho 3 dư 0 hoặc 1
Đúng 3
Bình luận (3)
a) n + 13 = n - 5 + 18
Để (n + 13) ⋮ (n - 5) thì 18 ⋮ (n - 5)
⇒ n - 5 ∈ Ư(18) = {-18; -9; -6; -3; -2; -1; 1; 2; 3; 6; 9; 18}
⇒ n ∈ {-13; -4; -1; 2; 3; 4; 6; 7; 8; 11; 14; 23}
Mà n ∈ ℕ và n > 5
⇒ n ∈ {6; 7; 8; 11; 14; 23}
b) 15 - 2n = -(2n - 15)
= -(2n + 2 - 17)
Để (15 - 2n) ⋮ (n + 1) thì 17 ⋮ (n + 1)
⇒ n + 1 ∈ Ư(17) = {-17; -1; 1; 17}
⇒ n ∈ {-18; -2; 0; 16}
Mà n ∈ ℕ và n ≤ 7
⇒ n = 0
c) (6n + 9) ⋮ (4n - 1)
⇒ 2.(6n + 9) ⋮ (4n - 1)
Ta có:
2.(6n + 9) = 12n + 18
= 12n - 3 + 21
= 3(4n - 1) + 21
Để (6n + 9) ⋮ (4n - 1) thì 21 ⋮ (4n - 1)
⇒ 4n - 1 ∈ Ư(21) = {-21; -7; -3; -1; 1; 3; 7; 21}
⇒ 4n ∈ {-20; -6; -2; 0; 2; 4; 8; 22}
⇒ n ∈ {-5; -3/2; -1/2; 0; 1/2; 1; 2; 11/2}
Mà n ∈ ℕ và n ≥ 1
⇒ n ∈ {1; 2}
Đúng 2
Bình luận (1)
Ta có:
\(7^{400}=\left(7^4\right)^{100}=\left(...1\right)^{100}=...1\)
Nên: \(7^{400}-1=...1-1=...0\)
Mà: \(...0\) ⋮ 5
\(\Rightarrow7^{400}-1\) ⋮ 5
Đúng 3
Bình luận (0)
Tìm chữ số tận cùng: 313^50
Dùng công thức 4n +1
Mọi số tự nhiên khi nâng lên lũy thừa bậc 4n +1 thì chữ số tận cùng k thay đổi
313=4.78+1 (4n+1 ko dư)
Chữ số tận cùng của 313 là 3 vậy
Chữ số tận cùng của \(313^{50}\)cũng là 3
Đúng 1
Bình luận (1)