Bài 1: Số phức

\(z^2-2\left(2m-1\right)z+m^2=0\)

Theo Vi - ét, ta có :

\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)

Ta có :

\(z^2_1+z_2^2=2\)

\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)

\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)

\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)

\(\Leftrightarrow14m^2-16m+2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)

Ta có phương trình bậc hai trên tập số phức:

z^2 - 2(2m-1)z + m^2 = 0

Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:

z1 + z2 = 2(2m-1) và z1z2 = m^2

Từ phương trình z1^2 + z2^2 = 2, ta suy ra:

(z1+z2)^2 - 2z1z2 = 4

Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:

(2(2m-1))^2 - 2m^2 = 4

Đơn giản hóa biểu thức ta có:

m^2 - 4m + 1 = 0

Suy ra:

m = 2 + √3 hoặc m = 2 - √3

Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.

Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.

Sử dụng BĐT trị tuyệt đối \(\left\{{}\begin{matrix}\left|x-y\right|\ge\left|x\right|-\left|y\right|\\\left|x-y\right|\ge\left|y\right|-\left|x\right|\end{matrix}\right.\)

 \(\Rightarrow-\left|x-y\right|+\left|y\right|\le\left|x\right|\le\left|x-y\right|+\left|y\right|\)

Thay \(x;y\) lần lượt bằng \(z\) và \(a+bi\) với chú ý \(\left|x-y\right|=\left|z-\left(a+bi\right)\right|=c\) rồi chuyển vế là ta được đánh giá nói trên

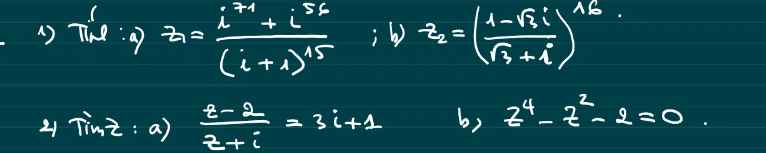
1.

\(z_1=\dfrac{i.\left(i^2\right)^{35}+\left(i^2\right)^{28}}{\left(i+1\right).\left[\left(i+1\right)^2\right]^7}=\dfrac{i.\left(-1\right)^{35}+\left(-1\right)^{28}}{\left(i+1\right)\left[i^2+2i+1\right]^7}\)

\(=\dfrac{-i+1}{\left(i+1\right)\left(2i\right)^7}=\dfrac{-i+1}{\left(i+1\right).2^7.i.\left(i^2\right)^3}=\dfrac{-i+1}{\left(i^2+i\right).2^7.\left(-1\right)^3}\)

\(=\dfrac{-i+1}{\left(-1+i\right).2^7.\left(-1\right)}=\dfrac{-i+1}{\left(-i+1\right).2^7}=\dfrac{1}{2^7}\)

b.

\(z_2=\left(\dfrac{1-\sqrt{3}i}{\sqrt{3}+i}\right)^{16}=\left(\dfrac{\left(1-\sqrt{3}i\right)\left(\sqrt{3}-i\right)}{\left(\sqrt{3}+i\right)\left(\sqrt{3}-i\right)}\right)^{16}\)

\(=\left(\dfrac{\sqrt{3}-4i+\sqrt{3}i^2}{3-i^2}\right)^{16}=\left(\dfrac{-4i}{4}\right)^{16}=\left(i\right)^{16}\)

\(=\left(i^2\right)^8=\left(-1\right)^8=1\)

2.

a.

\(\dfrac{z-2}{z+1}=3i+1\Leftrightarrow z-2=\left(3i+1\right)z+3i+1\)

\(\Leftrightarrow-3i.z=3i+3\)

\(\Leftrightarrow-i.z=i+1\)

\(\Leftrightarrow z=\dfrac{i+1}{-i}=\dfrac{i\left(i+1\right)}{-i^2}=i^2+i\)

\(\Leftrightarrow z=i-1\)

b.

\(z^4-z^2-2=0\Leftrightarrow\left(z^2+1\right)\left(z^2-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}z^2=-1\\z^2=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}z=\pm i\\z=\pm\sqrt{2}\end{matrix}\right.\)

Lời giải:

Đặt $z=a+bi$ với $a,b$ là các số thực

\(z^2=(a+bi)^2=a^2-b^2+2abi\) là phần thực

$\Leftrightarrow 2ab=0(1)$

\(2=|z-2-i|=|(a-2)+i(b-1)|=\sqrt{(a-2)^2+(b-1)^2}\)

\(\Leftrightarrow 4=(a-2)^2+(b-1)^2(2)\)

Từ $(1);(2)$ suy ra $(a,b)=(0,1);(2\pm \sqrt{3}, 0)$

Suy ra có 3 số phức thỏa mãn.

\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)

\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)

\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)

2.

Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?

Phần thực: \(a=0\) ; phần ảo: \(b=-\sqrt{2}\)

ta có : \(\left|z+1+i\right|=\left|z+2i\right|\Leftrightarrow\left(a+1\right)^2+\left(b+1\right)^2+a^2+\left(b+2\right)^2\)

\(\Leftrightarrow b=a-1\)

khí đó : \(P=\left|z-2-3i\right|+\left|z+1\right|=\sqrt{\left(a-2\right)^2+\left(b-3\right)^2}+\sqrt{\left(a+1\right)^2+b^2}\)

\(\Leftrightarrow P=\sqrt{\left(a-2\right)^2+\left(a-4\right)^2}+\sqrt{\left(a+1\right)^2+\left(a-1\right)^2}\ge\sqrt{\left(2a-1\right)^2+\left(2a-5\right)^2}\)

dấu "=" xảy ra khi \(\dfrac{a-2}{a+1}=\dfrac{a-4}{a-1}=k>0\) \(\Leftrightarrow a\in\varnothing\) \(\Rightarrow\) không có giá trị của \(P=a+2b\)

- là số phức và số phức liên hợp á bạn..