Cho tam giác ABC vuông tại A có đường cao là ah HP = 9 cm HC = 16 cm
a)tính AB AC ah
b)Gọi D và E lần lượt là hình chiếu vuông góc của h trên AB và AC. tứ giác AD he là hình gì
Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
a: BC=BH+CH=25cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH^2=HB*HC
\(AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AH=\sqrt{HB\cdot HC}=12\left(cm\right)\)
b: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết cạnh góc vuông AB=20cm, hình chiếu của AC lên cạnh huyền BC là HC=9cm. Tính diện tích tam giác ABC?
Tam giác ABC vuông tại A áp dụng đính lý cạnh góc vuông và hình chiếu ta có::
\(AB^2=BC\cdot HB=BC\cdot\left(BC-HC\right)\)
\(\Rightarrow20^2=BC^2-BC\cdot9\)
\(\Rightarrow BC^2-9BC-400=0\)
\(\Rightarrow BC^2+16BC-25BC-400=0\)
\(\Rightarrow BC\left(BC+16\right)-25\left(BC+16\right)=0\)
\(\Rightarrow\left(BC+16\right)\left(BC-25\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}BC+16=0\\BC-25=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}BC=-16\left(ktm\right)\\BC=25\left(tm\right)\end{matrix}\right.\)
Áp dụng hệ thức đường cao và hình chiếu ta có:
\(AH^2=HC\cdot HB\Rightarrow AH=\sqrt{HC\cdot\left(BC-HC\right)}\)
\(\Rightarrow AH=\sqrt{9\cdot\left(25-9\right)}=12\left(cm\right)\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot25\cdot12=150\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M,N lần lượt là hình chiếu của H lên AC, AB. CMR:
a,`AH^3 = BC.AM.AN`
b,`AH^2 = AN.NB+AM.MC`
cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là hình chiếu của D trên AB và AC . Chứng minh rằng DE2 = BD * CE*BC
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>AH=DE
BD*CE*BC
=BH^2/BA*CH^2/CA*BC
=AH^4/AH=AH^3
=DE^3
Đúng 0
Bình luận (0)
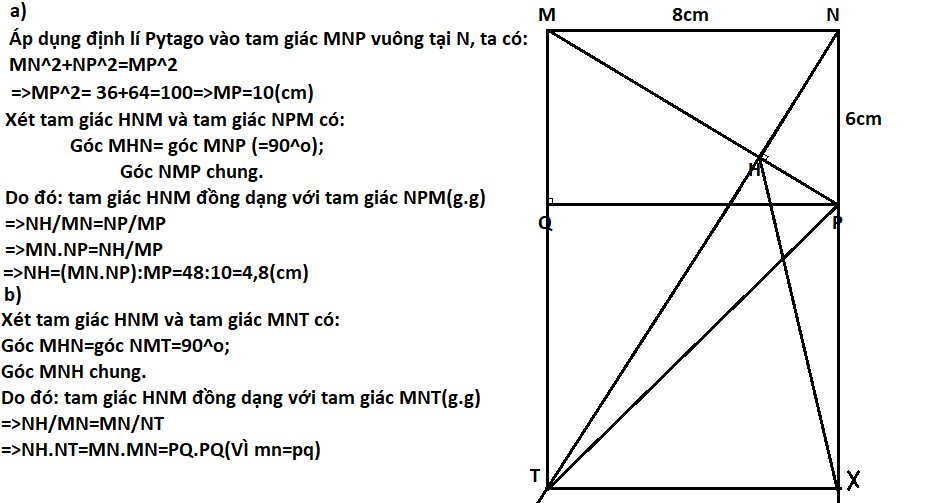
Cho hình chữ nhật MNPQ có MN=8cm, NP=6cm. Kẻ NH vuông góc với MP tại H, tia NH cắt đường thẳng MQ ở T
a. Tính NH
b. Chứng minh NH.NT=PQ.PQ
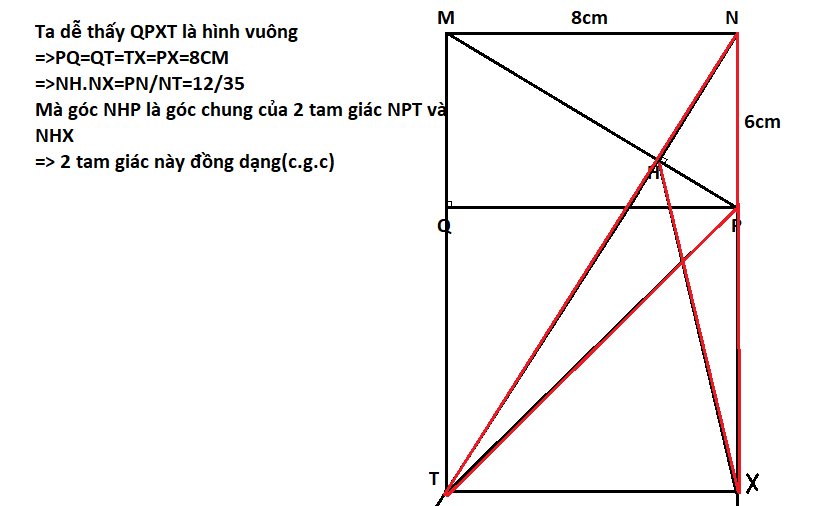
c. Kẻ TX vuông góc với NP tại X. Chứng minh Tam giác NPT đồng dạng với Tam giác NHX
cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết BD=15cm, CD=20cm. Tính BH,CH?
BC=15+20=35cm
BD/CD=3/4
=>AB/AC=3/4
BH/CH=(AB/AC)^2=9/16
=>BH/9=CH/16=35/25=1,4
=>BH=12,6cm; CH=22,4cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A đường cao AH, AD là phân giác góc A. Biết AB=6cm, BC=10cm. Tính BD,HD,DC,AD
Help
AC=căn 10^2-6^2=8cm
AH=6*8/10=4,8cm
\(AD=\dfrac{2\cdot6\cdot8}{6+8}\cdot cos45=\dfrac{24}{7}\sqrt{2}\left(cm\right)\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{24}{35}\left(cm\right)\)
AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=10/7
=>DB=30/7cm; DC=40/7cm
Đúng 0
Bình luận (0)
Bài 4. Cho đường tròn tâm O, đường kính AB = 10 cm và điểm C thuộc đường tròn sao cho AC=6 cm. Về CH vuông góc với AB tại H.
a) Chứng minh rằng tam giác ABC vuông tại C.
b) Tính HB và HC.
c) Trên tia đối của tia CA lấy điểm D sao cho CD= 2 cm. Gọi M là giao điểm của BD với đường tròn(M khác B). Chứng minh rằng CMD = CAB.
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
=>ΔCAB vuông tại C
b: CB=căn 10^2-6^2=8cm
HC=6*8/10=4,8cm
HA=CA^2/CB=3,6cm
HB=10-3,6=6,4cm
c: A,C,M,B nội tiếp
=>góc CMB+góc CAB=180 độ
mà góc CMB+góc CMD=180 độ
nên góc CMD=góc CAB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có BC =12 cm . Tính chiều dài hai cạnh góc vuông biết AB 2/3 AC
Ta có \(\Delta ABC\) vuông tại A nên:
\(BC^2=AB^2+AC^2\)
Mà: \(AB=\dfrac{2}{3}AC\)
\(\Rightarrow BC^2=\left(\dfrac{2}{3}AC\right)^2+AC^2\)
\(\Rightarrow12^2=\left(\dfrac{2}{3}AC\right)^2+AC\)
\(\Rightarrow144=\dfrac{4}{9}AC^2+AC^2\)
\(\Rightarrow144=\dfrac{13}{9}AC^2\)
\(\Rightarrow AC^2=\dfrac{144}{\dfrac{13}{9}}\approx100\)
\(\Rightarrow AC\approx\sqrt{100}\approx10\left(cm\right)\)
Ta có \(AC=10cm\Rightarrow AB=\dfrac{2}{3}AC=\dfrac{2}{3}\cdot10\approx6,6\left(cm\right)\)
Vậy: ....
Đúng 0
Bình luận (1)
Giúp mình câu b và c thôi ạ. Mình cảm ơn Cho Tam giác nhọn ABC (AB