Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \(34^0\) và bóng của một tháp trên mặt đất dài 86m (h.30). Tính chiều cao của tháp (làm tròn đến mét)
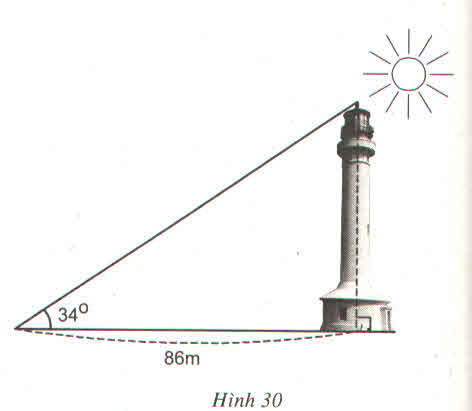
Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \(34^0\) và bóng của một tháp trên mặt đất dài 86m (h.30). Tính chiều cao của tháp (làm tròn đến mét)

Giải tam giác ABC vuông tại A, biết rằng :
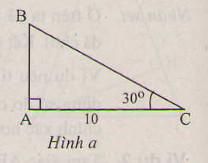
a) \(b=10cm,\widehat{C}=30^0\)
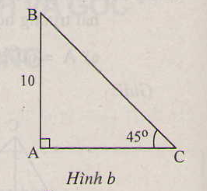
b) \(c=10cm,\widehat{C}=45^0\)
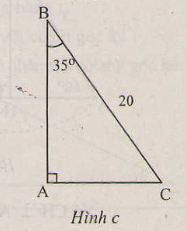
c) \(a=20cm,\widehat{B}=35^0\)
d) \(c=21cm,b=18cm\)
a) (H.a)
.
b) (H.b)
c) (H.c)
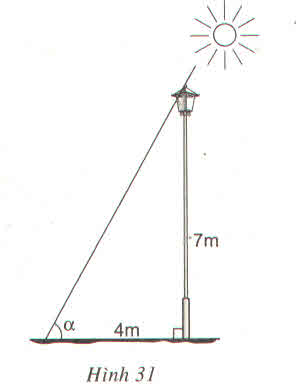
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc \(\alpha\) trong hình 31)
Một khúc sông rộng khoảng 250m. Một chiếc đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu độ ? (góc \(\alpha\) trong hình 32)

Cho tam giác ABC, trong đó \(BC=11cm,\widehat{ABC}=38^0,\widehat{ACB}=30^0\). Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính :
a) Đoạn thẳng AN
b) Cạnh AC
Gợi ý : Kẻ BK vuông góc với AC
a) Kẻ
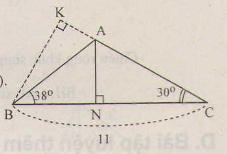
Ta được: và
Xét tam giác KBC vuông tại K có:
Xét tam giác KBA vuông tại K có:
Xét tam giác ABN vuông tại N có:
b) Xét tam giác ANC vuông tại N có
Trong hình 33 :
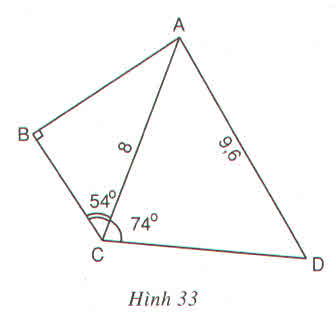
\(AC=8cm,AD=9,6cm,\widehat{ABC}=90^0,\widehat{ACB}=54^0;\widehat{ACD}=74^0\)
Hãy tính :
a) AB
b) \(\widehat{ADC}\)
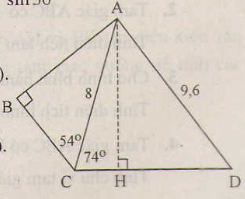
a) Xét tam giác ABC vuông tại B có:
b) Vẽ CD. Xét tam giác ACH có:
Xét tam giác AHD vuông tại H có:
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.
Trả lời bởi Nhật LinhMột con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy rất mạnh mất 5 phút. Biết đường đi của con thuyền tạo với bờ một góc \(70^0\). Từ đó đã có thể tính được chiều rộng của khúc sông chưa ? Nếu có thể hãy tính kết quả (làm tròn đến mét)
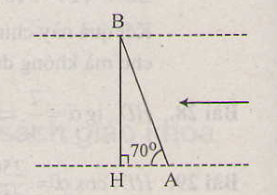
Gọi AB là đoạn đường mà con thuyền đi được trong 5 phút, BH là chiều rộng của khúc sông.
Xét tam giác ABH vuông tại H, biết cạnh huyền AB và một góc nhọn thì có thể tính được BH.
Quãng đường thuyền đi trong 5 phút là:
Chiều rộng khúc sông là: .
Trả lời bởi Nhật LinhTam giác ABC vuông tại A có \(AB=21cm,\widehat{C}=40^0\). Hãy tính các độ dài :
a) AC
b) BC
c) Phân giác BD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)
Trả lời bởi BW_P&ACho hình 16.
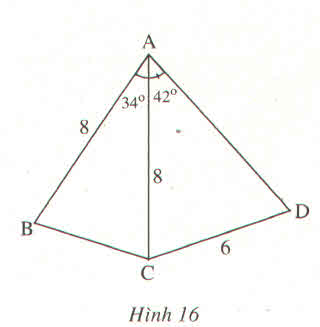
Biết \(AB=AC=8cm,CD=6cm,\widehat{BAC}=34^0,\widehat{CAD}=42^0\). Hãy tính :
a) Độ dài cạnh BC
b) \(\widehat{ADC}\)
c) Khoảng cách từ điểm B đến cạnh AD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, \(\widehat{BAC}=20^0\). Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần ;
\(\sin20^0\approx0,3420;\cos20^0\approx0,9397;tg20^0\approx0,3640\)
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Kẻ BH vuông góc với AC
Xét ΔABH vuông tại H có \(BH=AB\cdot\sin A\simeq1,7101\left(cm\right)\)
\(S_{ABC}=\dfrac{BH\cdot AC}{2}=6.8404\left(cm^2\right)\)
Trả lời bởi Nguyễn Lê Phước Thịnh
Chiều cao của tháp là 86⋅tg34∘≈58(m)86⋅tg34∘≈58(m).
Trả lời bởi Nhật Linh