
Bài 1: Lũy thừa
a) 3/12 và 3/12
b) 16/24 và 18/24
c) 12/9 và -12/9
d) 9/-15 và 9/-15
Đúng 0
Bình luận (0)
Giúp e câu này đi ạ 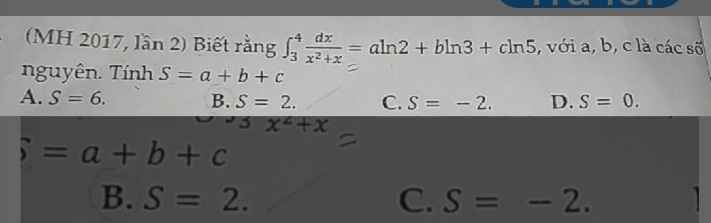
\(\int\limits^4_3\dfrac{dx}{x^2+x}=\int\limits^4_3\dfrac{dx}{x\left(x+1\right)}=\int\limits^4_3\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)dx=\left[lnx-ln\left(x+1\right)\right]|^4_3\)
\(=ln4-ln5-\left(ln3-ln4\right)=2ln4-ln3-ln5\)
\(=4ln2-ln3-ln5\Rightarrow a=4;b=c=-1\)
\(\Rightarrow S=2\)
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
Cho a;b;c >=0 thỏa mãn \(a^2+b^2+c^2=3\)
\(CMR:\dfrac{a}{b+2}+\dfrac{b}{c+2}+\dfrac{c}{a+2}\le1\)
\(\Leftrightarrow a\left(a+2\right)\left(c+2\right)+b\left(a+2\right)\left(c+2\right)+c\left(b+2\right)\left(c+2\right)\le\left(a+2\right)\left(b+2\right)\left(c+2\right)\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)+ab^2+bc^2+ca^2\le8+abc\)
\(\Leftrightarrow ab^2+bc^2+ca^2\le2+abc\)
Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)
\(\Rightarrow\left(a-b\right)\left(b-c\right)\ge0\)
\(\Leftrightarrow ab+bc\ge b^2+ac\)
\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)
\(\Rightarrow ab^2+bc^2+ca^2\le bc^2+a^2b+abc=b\left(a^2+c^2\right)+abc=b\left(2-b^2\right)+abc\)
\(=2+abc-\left(b-1\right)^2\left(b+2\right)\le2+abc\) (đpcm)
Đúng 1
Bình luận (0)
1. Giá trị của biểu thức P left(1+sqrt{3}right)^{2016}.left(3-sqrt{3}right)^{2016} bằng?2. Cho a là 1 một số dương, biểu thức a^{dfrac{2}{3}}.sqrt{a} viết dưới dạng lũy thừa với số mũ hữu tỉ là?3. Viết biểu thức Q sqrt{x}.sqrt[3]{x}.sqrt[6]{x^5} với x 0 dưới dạng lũy thừa với số mũ hữu tỉ là?
Đọc tiếp
1. Giá trị của biểu thức P = \(\left(1+\sqrt{3}\right)^{2016}.\left(3-\sqrt{3}\right)^{2016}\) bằng?
2. Cho a là 1 một số dương, biểu thức \(a^{\dfrac{2}{3}}.\sqrt{a}\) viết dưới dạng lũy thừa với số mũ hữu tỉ là?
3. Viết biểu thức Q = \(\sqrt{x}.\sqrt[3]{x}.\sqrt[6]{x^5}\) với x > 0 dưới dạng lũy thừa với số mũ hữu tỉ là?
\(1,P=\left(1+\sqrt{3}\right)^{2016}\cdot\left(\sqrt{3}-1\right)^{2016}\cdot\left(\sqrt{3}\right)^{2016}\\ P=\left(1-3\right)^{2016}\cdot\left(\sqrt{3}\right)^{2016}=\left(-2\right)^{2016}\cdot\left(\sqrt{3}\right)^{2016}=\left(2\sqrt{3}\right)^{2016}\)
Đúng 1
Bình luận (1)
2.
\(a^{\dfrac{2}{3}}\sqrt{a}=a^{\dfrac{2}{3}}.a^{\dfrac{1}{2}}=a^{\dfrac{2}{3}+\dfrac{1}{2}}=a^{\dfrac{7}{6}}\)
3.
\(Q=x^{\dfrac{1}{2}}.x^{\dfrac{1}{3}}.x^{\dfrac{5}{6}}=x^{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{5}{6}}=x^{\dfrac{5}{3}}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức P = \(\dfrac{x^{\dfrac{1}{6}}.\sqrt[3]{x^4}.\sqrt[4]{x^5}}{\sqrt{x^3}}\) với x > 0
\(P=\dfrac{x^{\dfrac{1}{6}}.x^{\dfrac{4}{3}}.x^{\dfrac{5}{4}}}{x^{\dfrac{3}{2}}}=x^{\dfrac{1}{6}+\dfrac{4}{3}+\dfrac{5}{4}-\dfrac{3}{2}}=x^{\dfrac{5}{4}}\)
Đúng 1
Bình luận (0)
1. Biết \(\dfrac{x^{a^2}}{x^{b^2}}=x^{16}\) với x>1 và a+b = 2. Tính giá trị của biểu thức M =a-b
2. Cho a,b >0, viết \(a^{\dfrac{2}{3}}.\sqrt{a}\) về dạng \(a^x\) và \(\sqrt[3]{b\sqrt{b\sqrt{b}}}\) về dạng by. Tính 6x+12y?
1.
\(\dfrac{x^{a^2}}{x^{b^2}}=x^{16}\Leftrightarrow x^{a^2-b^2}=x^{16}\Rightarrow a^2-b^2=16\)
\(\Rightarrow\left(a-b\right)\left(a+b\right)=16\Rightarrow a-b=8\)
2.
\(a^{\dfrac{2}{3}}.a=a^{\dfrac{2}{3}+1}=a^{\dfrac{5}{3}}\Rightarrow x=\dfrac{5}{3}\)
\(\sqrt[3]{b\sqrt[]{b\sqrt[]{b}}}=\sqrt[3]{b\sqrt[4]{b^3}}=\sqrt[12]{b^4.b^3}=b^{\dfrac{7}{12}}\Rightarrow y=\dfrac{7}{12}\)
\(\Rightarrow6x+12y=17\)
Đúng 1
Bình luận (0)
1. Rút gọn biểu thức với P = \(\dfrac{x^{\dfrac{1}{6}}.\sqrt[3]{x^4}.\sqrt[4]{5}}{\sqrt{x^3}}\) với x>0
2. Với x> 0, hãy rút gọn biểu thức: P = \(\sqrt{x\sqrt{x\sqrt{x\sqrt{x\sqrt{x}}}}}:x^{\dfrac{9}{16}}\)
\(1,P=\dfrac{\dfrac{x}{6}\cdot x\sqrt{x}\cdot\sqrt[4]{5}}{x\sqrt{x}}=\dfrac{x}{6}\cdot\sqrt[4]{5}\)
Đúng 0
Bình luận (0)
1.
Xem lại đề, chỗ \(\sqrt[4]{5}\) trên tử số
2.
\(P=\sqrt[4]{x^2.x\sqrt[]{x\sqrt[4]{x^3}}}:x^{\dfrac{9}{16}}=\sqrt[4]{x^3\sqrt[8]{x^4.x^3}}:x^{\dfrac{9}{16}}=\sqrt[4]{x^3.x^{\dfrac{7}{8}}}:x^{\dfrac{9}{16}}\)
\(=\sqrt[4]{x^{\dfrac{31}{8}}}:x^{\dfrac{9}{16}}=x^{\dfrac{31}{32}}:x^{\dfrac{9}{16}}=x^{\dfrac{31}{32}-\dfrac{9}{16}}=x^{\dfrac{13}{32}}\)
Đúng 1
Bình luận (0)
Cho 0<a ≠ 1.Rút gọn biểu thức: P= \(\dfrac{\left(a^3\right)^4}{a^2.a^{\dfrac{3}{2}}}\)
\(P=\dfrac{a^{3.4}}{a^{2+\dfrac{3}{2}}}=\dfrac{a^{12}}{a^{\dfrac{7}{2}}}=a^{12-\dfrac{7}{2}}=a^{\dfrac{17}{2}}\)
Đúng 1
Bình luận (0)




