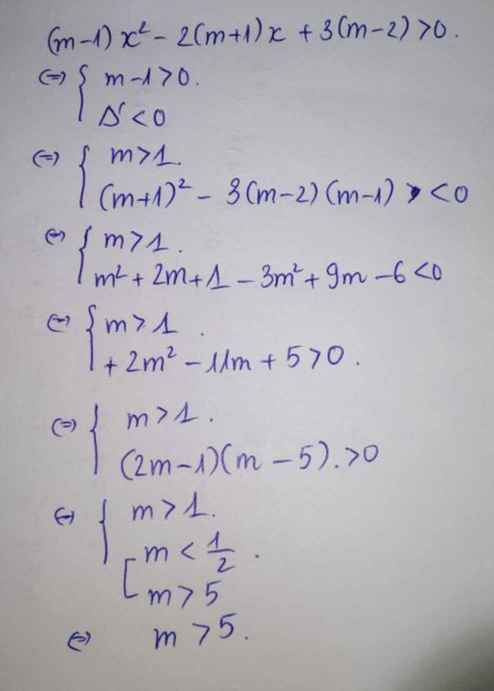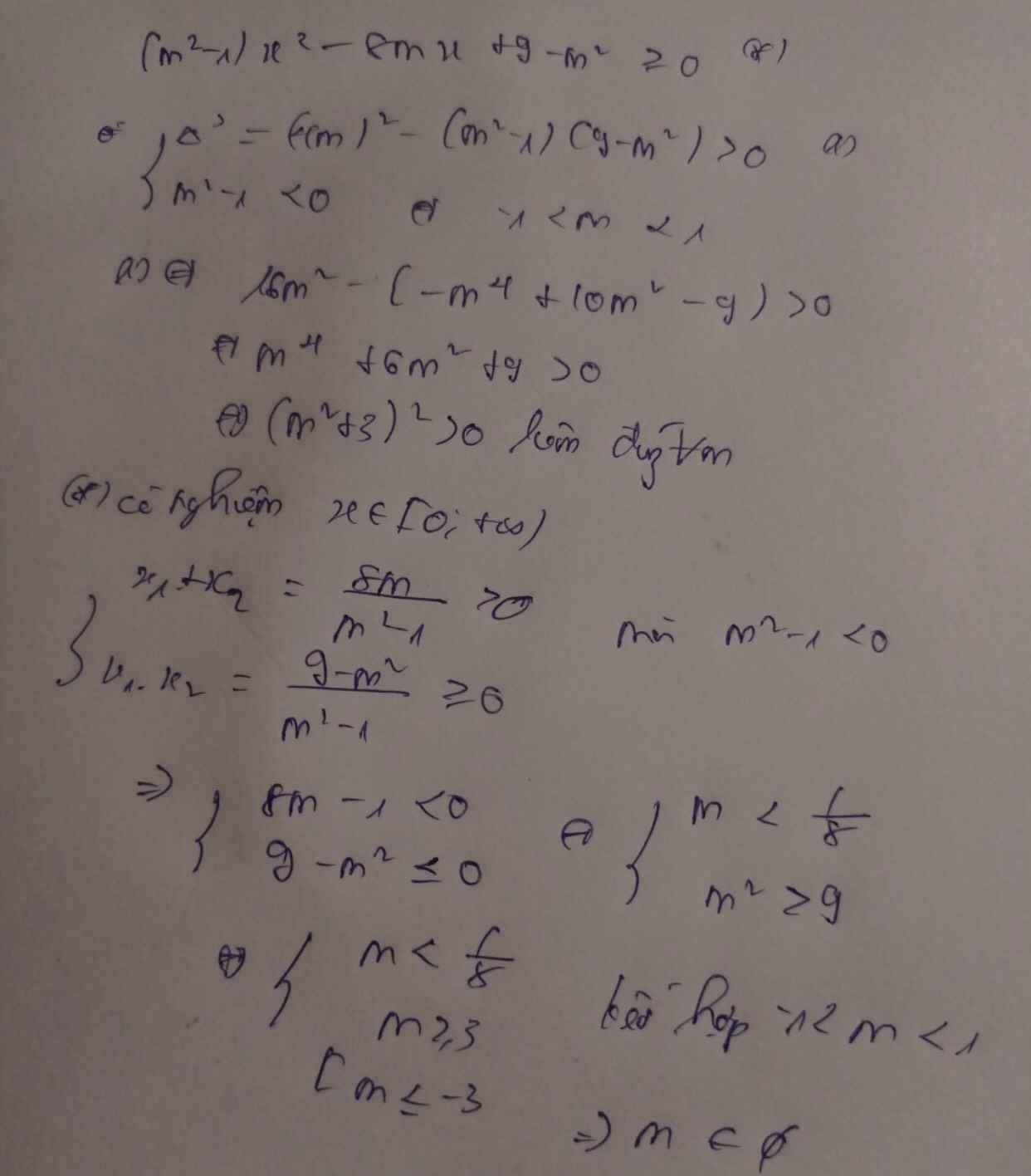§5. Dấu của tam thức bậc hai
Đề bài yêu cầu điều gì em nhỉ?
Đúng 0
Bình luận (0)
Giúp mình vs
\(\Delta=\left(m+3\right)^2-4=m^2+6m+5=\left(m+1\right)\left(m+5\right)\)
a: Để f(x)>0 thì (m+1)(m+5)<0
=>-5<m<-1
b: để f(x)>=0 thì (m+1)(m+5)<=0
=>-5<=m<=-1
c: Để f(x) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m<-5 hoặc m>-1
Đúng 1
Bình luận (0)
6.17
\(x^2+\left(m+1\right)x+2m+3>0;\forall x\) khi và chỉ khi:
\(\Delta=\left(m+1\right)^2-4\left(2m+3\right)< 0\)
\(\Leftrightarrow m^2-6m-11< 0\)
\(\Rightarrow3-2\sqrt{5}< m< 3+2\sqrt{5}\)
6.18
Do đề không cho nên coi \(g=10m/s^2\)
Độ cao của vật tại thời điểm t giây được tính theo phương trình:
\(h=320-\left(20t+5t^2\right)\)
Vật đó cách mặt đất không quá 100m
\(\Rightarrow320-\left(20t+5t^2\right)\le100\)
\(\Leftrightarrow t^2+4t-44\ge0\)
\(\Rightarrow t\ge-2+4\sqrt{3}\) (giây)
Đúng 1
Bình luận (0)

help me !!!!!!!!!!!!!!
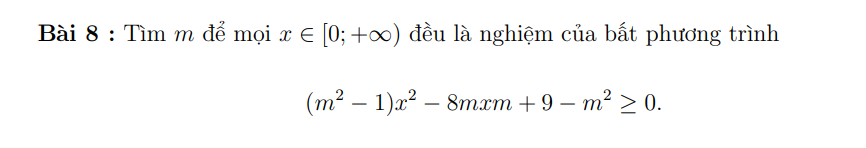
help meeeeee
\(f\left(x\right)=\left(m^2-1\right)x^2-8mx+9-m^2\ge0\)
\(TH1:m^2-1=0\Rightarrow m=\pm1\)
\(m=1\Rightarrow bpt\Leftrightarrow-8x+8\ge0\Leftrightarrow x\le1\left(loại\right)\)
\(m=-1\Rightarrow bpt\Leftrightarrow8x+8\ge0\Leftrightarrow x\ge-1\left(tm\right)\)
\(TH2:m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
\(\Delta=\left(8m\right)^2-4\left(9-m^2\right)\left(m^2-1\right)< 0\Leftrightarrow4x^4+24x^2+36=\left(2x^2\right)^2+2.2x^2.6+6^2=\left(2x^2+6\right)^2>0\left(\forall m\right)\)
\(\Rightarrow x1< x2\le0\Leftrightarrow\)\(\left\{{}\begin{matrix}x1x2\ge0\\x1+x2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}9-m^2\ge0\\8m< 0\end{matrix}\right.\)
\(\Leftrightarrow-3\le m< 0\Rightarrow-3\le m< -1\)
\(TH3:m^2-1< 0\Leftrightarrow-1< m< 1\)
\(f\left(x\right)\ge0\Leftrightarrow\Delta\le0\Leftrightarrow\left(2x^2+6\right)^2\le0\left(vô-lí\right)\)
\(\Rightarrow-3\le m\le-1\)
Đúng 0
Bình luận (0)
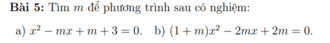
giúp mk vs...
a: Để phương trình có nghiệm thì \(m^2-4\left(m+3\right)>=0\)
\(\Leftrightarrow\left(m-6\right)\left(m+2\right)>=0\)
=>m>=6 hoặc m<=-2
b: Trường hợp 1: m=-1
Pt sẽ là \(-2\cdot\left(-1\right)x+2\cdot\left(-1\right)=0\)
=>2x-2=0
hay x=1
=>Nhận
Trường hợp 2: m<>-1
\(\Delta=\left(-2m\right)^2-4\cdot2m\left(m+1\right)\)
\(=4m^2-8m\left(m+1\right)\)
\(=-4m^2-8m=-4m\left(m+2\right)\)
Để phương trình có nghiệm thì m(m+2)<=0
=>-2<=m<=0
Đúng 0
Bình luận (0)
a. \(x^2+bx+9>0\)
<=> \(x\left(x+b\right)+9>0\) , pt này đúng với mọi giá trị x và b thuộc Z
Đúng 3
Bình luận (0)