Ôn tập chương IV
Nội dung lý thuyết
Các phiên bản khácI. BẤT ĐẲNG THỨC
1. Ôn tập về bất đẳng thức
- Các mệnh đề có dạng "\(a< b\)" hoặc "\(a>b\)" được gọi là các bất đẳng thức ngặt, các mệnh đề dạng "\(a\ge b\)" hoặc "\(a\le b\)" được gọi là các bất đẳng thức không ngặt.
- Nếu mệnh đề "\(a< b\Rightarrow c< d\)" là mệnh đề đúng thì ta nói bất đẳng thức \(c< d\) là bất đẳng thức hệ quả của bất đẳng thức \(a< b\) và cũng viết là \(a< b\Rightarrow c< d\).
- Tính chất: \(a< b\) và \(b< c\) \(\Rightarrow\) \(a< c\) (Tính chất bắc cầu)
\(a< b\), \(c\) tuỳ ý \(\Rightarrow\) \(a+c< b+c\) (Tính chất cộng hai vế bất đẳng thức với một số).
- Nếu bất đẳng thức \(a< b\) là hệ quả của bất đẳng thức \(c< d\) và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là \(a< b\Leftrightarrow c< d\).
- Tính chất của bất đẳng thức:
| Điều kiện | Nội dung | Tên gọi |
| \(a< b\) \(\Leftrightarrow\) \(a+c< b+c\) | Cộng hai vế của bất đẳng thức với một số | |
| \(c>0\) | \(a< b\Leftrightarrow ac< bc\) | Nhân 2 vế bất đẳng thức với một số dương |
| \(c< 0\) | \(a< b\Leftrightarrow ac>bc\) | Nhân 2 vế bất đẳng thức với một số âm |
| \(\left\{{}\begin{matrix}a< b\\c< d\end{matrix}\right.\Rightarrow a+c< b+d\) | Cộng hai bất đẳng thức cùng chiều | |
| \(a>0\), \(c>0\) | \(\left\{{}\begin{matrix}a< b\\c< d\end{matrix}\right.\Rightarrow ac< bd\) | Nhân hai bất đẳng thức cùng chiều |
| \(n\in N\)* | \(a< b\) \(\Rightarrow a^{2n+1}< b^{2n+1}\) | Nâng hai vế của bất đẳng thức lên một luỹ thừa |
| \(n\in N\)* và \(a>0\) | \(a< b\) \(\Rightarrow a^{2n}< b^{2n}\) | Nâng hai vế của bất đẳng thức lên một luỹ thừa |
| \(a>0\) | \(a< b\) \(\Rightarrow\sqrt{a}< \sqrt{b}\) | Khai căn hai vế của một bất đẳng thức |
| \(a< b\) \(\Rightarrow\sqrt[3]{a}< \sqrt[3]{b}\) | Khai căn hai vế của một bất đẳng thức |
Các tính chất trên đúng cho cả các bất đẳng thức không ngặt.
@71423@
2. Bất đẳng thức Cô-si và các hệ quả
- Định lí: Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng: \(\sqrt{ab}\le\dfrac{a+b}{2}\), \(\forall a,b\ge0\).
Đẳng thức \(\sqrt{ab}=\dfrac{a+b}{2}\) xảy ra khi và chỉ khi \(a=b\).
- Hệ quả 1: Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng \(2\).
\(a+\dfrac{1}{a}\ge2,\forall a>0\)
- Hệ quả 2: Nếu \(x,y\) cùng dương và có tổng không đổi thì tích \(xy\) lớn nhất khi và chỉ khi \(x=y\).
Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
- Hệ quả 3: Nếu \(x,y\) cùng dương và có tích không đổi thì tổng \(x+y\) nhỏ nhất khi và chỉ khi \(x=y\).
Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
3. Bất đẳng thức chứa dấu giá trị tuyệt đối
Từ định nghĩa giá trị tuyệt đối, ta sử dụng các tính chất sau:
| Điều kiện | Nội dung |
| \(\left|x\right|\ge0\), \(\left|x\right|\ge x\), \(\left|x\right|\ge-x\) | |
| \(a>0\) | \(\left|x\right|\le a\Leftrightarrow-a\le x\le a\) |
| \(a>0\) | \(\left|x\right|\ge a\) \(\Leftrightarrow x\le-a\) hoặc \(x\ge a\) |
| \(\left|a\right|-\left|b\right|\le\left|a+b\right|\le\left|a\right|+\left|b\right|\) |
@1895259@
II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH MỘT ẨN
1. Bất phương trình một ẩn
- Bất phương trình ẩn \(x\) là mệnh đề chứa biến có dạng \(f\left(x\right)< g\left(x\right)\) (\(f\left(x\right)\le g\left(x\right)\)), trong đó \(f\left(x\right)\) và \(g\left(x\right)\) là các biểu thức của \(x\).
Ta gọi \(f\left(x\right)\) và \(g\left(x\right)\) lần lượt là vế trái và vế phải của bất phương trình.
Số thực \(x_0\) sao cho \(f\left(x_0\right)< g\left(x_0\right)\) (\(f\left(x_0\right)\le g\left(x_0\right)\)) là một mệnh đề đúng được gọi là một nghiệm của bất phương trình.
Giải bất phương trình là tìm tập nghiệm của nó, khi tập nghiệm rỗng thì ta nói bất phương trình vô nghiệm.
- Tương tự đối với phương trình, ta gọi các điều kiện của ẩn số \(x\) để \(f\left(x\right)\) và \(g\left(x\right)\) có nghĩa là điều kiện xác định (hay gọi tắt là điều kiện) của bất phương trình.
- Trong một bất phương trình, ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số.
Giải và biện luận bất phương trình chứa tham số là xét xem với các giá trị nào của tham số bất phương trình vô nghiệm, bất phương trình có nghiệm và tìm các nghiệm đó.
2. Hệ bất phương trình một ẩn
- Hệ bất phương trình ẩn \(x\) gồm một số bất phương trình ẩn \(x\) mà ta phải tìm các nghiệm chung của chúng.
Mỗi giá trị của \(x\) đồng thời là nghiệm của tất cả các bất phương trình của hệ được gọi là một nghiệm của hệ bất phương trình đã cho.
Giải hệ bất phương trình là tìm tập nghiệm của nó.
Để giải một hệ bất phương trình ta giải từng bất phương trình rồi lấy giao của các tập nghiệm.
3. Một số phép biến đổi bất phương trình
- Hai bất phương trình (hoặc hệ bất phương trình) có cùng tập nghiệm (kể cả tập rỗng) được gọi là hai bất phương trình tương đương (hoặc hai hệ bất phương trình tương đương) và được kí hiệu bởi dấu "\(\Leftrightarrow\)".
- Để giải một bất phương trình (hoặc hệ bất phương trình) ta liên tiếp biến đổi nó thành các bất phương trình (hệ bất phương trình) tương đương cho đến khi được bất phương trình (hệ bất phương trình) đơn giản nhất mà ta có thể viết ngay tập nghiệm. Các phép biến đổi như vậy được gọi là các phép biến đổi tương đương.
Ví dụ: \(\left\{{}\begin{matrix}3-x\ge0\\x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\ge x\\x\ge-1\end{matrix}\right.\Leftrightarrow-1\le x\le3\)
- Phép cộng (trừ): Cộng (trừ) hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình ta được một bất phương trình tương đương.
\(P\left(x\right)< Q\left(x\right)\Leftrightarrow P\left(x\right)+f\left(x\right)< Q\left(x\right)+f\left(x\right)\)
Nhận xét: Chuyển vế và đổi dấu một hạng tử trong một bất phương trình ta được một bất phương trình tương đương: \(P\left(x\right)< Q\left(x\right)+f\left(x\right)\Leftrightarrow P\left(x\right)-f\left(x\right)< Q\left(x\right)\)
- Phép nhân (chia):
+ Nhân (chia) hai vế của một bất phương trình với cùng một biểu thức luôn nhận giá trị dương (mà không làm thay đổi điều kiện của bất phương trình) ta được một bất phương trình tương đương.
\(P\left(x\right)< Q\left(x\right)\Leftrightarrow P\left(x\right).f\left(x\right)< Q\left(x\right).f\left(x\right)\), nếu \(f\left(x\right)>0,\forall x\)
+ Nhân (chia) hai vế của một bất phương trình với cùng một biểu thức luôn nhận giá trị âm (mà không làm thay đổi điều kiện của bất phương trình) và đổi chiều bất phương trình ta được một bất phương trình tương đương.
\(P\left(x\right)< Q\left(x\right)\Leftrightarrow P\left(x\right).f\left(x\right)>Q\left(x\right).f\left(x\right)\), nếu \(f\left(x\right)< 0,\forall x\)
- Bình phương: Bình phương hai vế của một bất phương trình có hai vế không âm mà không là thay đổi điều kiện của nó ta được một bất phương trình tương đương.
\(P\left(x\right)< Q\left(x\right)\Leftrightarrow P^2\left(x\right)< Q^2\left(x\right)\), nếu \(P\left(x\right)\ge0,Q\left(x\right)\ge0,\forall x\)
- Các chú ý:
+ Khi biến đổi các biểu thức ở hai vế của một bất phương trình thì điều kiện của bất phương trình có thể bị thay đổi. Vì vậy, để tìm nghiệm của một bất phương trình ta phải tìm các giá trị của \(x\) thoả mãn điều kiện của bất phương trình đó và là nghiệm của bất phương trình mới.
+ Khi nhân (chia) hai vế của bất phương trình \(P\left(x\right)< Q\left(x\right)\) với biểu thức \(f\left(x\right)\) ta cần lưu ý đến điều kiện về dấu của \(f\left(x\right)\). Nếu \(f\left(x\right)\) nhận cả giá trị dương và giá trị âm thì ta phải lần lượt xét các trường hợp. Mỗi trường hợp dẫn đến một hệ bất phương trình.
+ Khi giải bất phương trình \(P\left(x\right)< Q\left(x\right)\) mà phải bình phương hai vế thì ta lần lượt xét hai trường hợp:
Nếu \(P\left(x\right),Q\left(x\right)\) cùng có giá trị không âm, ta bình phương hai vế của bất phương trình.
Nếu \(P\left(x\right),Q\left(x\right)\) cùng có giá trị âm ta viết \(P\left(x\right)< Q\left(x\right)\Leftrightarrow-P\left(x\right)>-Q\left(x\right)\) rồi mới bình phương hai vế của bất phương trình mới.
III. DẤU CỦA NHỊ THỨC BẬC NHẤT
1. Định lí về dấu của nhị thức bậc nhất
- Nhị thức bậc nhất đối với \(x\) là biểu thức dạng \(f\left(x\right)=ax+b\) trong đó \(a,b\) là hai số đã cho, \(a\ne0\).
- Định lí: Nhị thức \(f\left(x\right)=ax+b\) có giá trị cùng dấu với hệ số \(a\) khi \(x\) lấy các giá trị trong khoảng \(\left(-\dfrac{b}{a};+\infty\right)\), trái dấu với hệ số \(a\) khi \(x\) lấy các giá trị trong khoảng \(\left(-\infty;-\dfrac{b}{a}\right)\).
- Bảng xét dấu của nhị thức bậc nhất:
| \(x\) | \(-\infty\) \(-\dfrac{b}{a}\) \(+\infty\) |
| \(f\left(x\right)=ax+b\) | trái dấu với \(a\) \(0\) cùng dấu với \(a\) |
- Khi \(x=-\dfrac{b}{a}\) thì \(f\left(x\right)=0\), ta nói \(x_0=-\dfrac{b}{a}\) là nghiệm của nhị thức \(f\left(x\right)\).
Ví dụ: Bảng xét dấu của nhị thức \(f\left(x\right)=2x+3\):
| \(x\) | \(-\infty\) \(-\dfrac{3}{2}\) \(+\infty\) |
| \(f\left(x\right)=2x+3\) | - \(0\) + |
- Giả sử \(f\left(x\right)\) là một tích (hoặc một thương) của những nhị thức bậc nhất. Áp dụng định lí về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử. Lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong \(f\left(x\right)\) ta suy ra được dấu của \(f\left(x\right)\).
2. Áp dụng vào giải bất phương trình
- Bất phương trình tích, bất phương trình chứa ẩn ở mẫu:
Ví dụ: Ta có thể giải bất phương trình \(\dfrac{1}{1-x}\ge1\) như sau:
Điều kiện: \(x\ne1\)
\(\dfrac{1}{1-x}\ge1\) \(\Leftrightarrow\dfrac{1}{1-x}-1\ge0\Leftrightarrow\dfrac{x}{1-x}\ge0\)
Bảng xét dấu:
| \(x\) | \(-\infty\) - 0 + 1 + \(+\infty\) |
| \(1-x\) | + \(|\) + \(|\)\(|\) - |
| \(\dfrac{x}{1-x}\) | - 0 + \(|\)\(|\) - |
Vậy bất phương trình đã cho có nghiệm là \(0\le x< 1\).
- Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối: Ta áp dụng tính chất của giá trị tuyệt đối để giải bất phương trình:
\(\left|f\left(x\right)\right|\le a\Leftrightarrow-a\le f\left(x\right)\le a\), với \(a>0\)
\(\left|f\left(x\right)\right|\ge a\Leftrightarrow\left[{}\begin{matrix}f\left(x\right)\ge a\\f\left(x\right)\le-a\end{matrix}\right.\), với \(a>0\).
IV. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn \(x,y\) có dạng tổng quát là \(ax+by\le c\) (1)
(hoặc \(ax+by< c\), \(ax+by\ge c\), \(ax+by>c\)), trong đó \(a,b,c\) là những số thực đã cho, \(a\) và \(b\) không đồng thời bằng \(0\).
Ví dụ: \(3x+2y< 1\) là một bất phương trình bậc nhất hai ẩn \(x,y\), cặp số \(\left(x;y\right)=\left(1;-2\right)\) là một nghiệm của bất phương trình.
- Trong mặt phẳng toạ độ \(Oxy\), tập hợp các điểm có toạ độ là nghiệm bất phương trình (1) được gọi la miền nghiệm của nó.
- Quy tắc thực hành biểu diễn hình học tập nghiệm của bất phương trình \(ax+by\le c\) như sau (tương tự cho bất phương trình \(ax+by\ge c\)):
Bước 1: Trên mặt phẳng toạ độ \(Oxy\), vẽ đường thẳng \(\Delta\): \(ax+by=c\)
Bước 2: Lấy một điểm \(M_0\left(x_0;y_0\right)\) không thuộc \(\Delta\) (ta thường lấy gốc toạ độ \(O\))
Bước 3: Tính \(ax_0+by_0\) và so sánh \(ax_0+by_0\) với \(c\)
Bước 4: Kết luận:
Nếu \(ax_0+by_0< c\) thì nửa mặt phẳng bờ \(\Delta\) chứa \(M_0\left(x_0;y_0\right)\) là miền nghiệm của bất phương trình \(ax+by\le c\) ;
Nếu \(ax_0+by_0>c\) thì nửa mặt phẳng bờ \(\Delta\) không chứa \(M_0\left(x_0;y_0\right)\) là miền nghiệm của bất phương trình \(ax+by\le c\).
- Chú ý: Miền nghiệm của bất phương trình \(ax+by\le c\) bỏ đi đường thẳng \(ax+by=c\) là miền nghiệm của bất phương trình \(ax+by< c\).
2. Hệ bất phương trình bậc nhất hai ẩn
- Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn \(x,y\) mà ta phải tìm các nghiệm chung của của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.
- Cũng như bất phương trình bậc nhất hai ẩn, ta cũng có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.
V. DẤU CỦA TAM THỨC BẬC HAI
- Tam thức bậc hai đối với \(x\) là biểu thức có dạng \(f\left(x\right)=ax^2+bx+c\), trong đó \(a,b,c\) là những hệ số, \(a\ne0\).
- Định lí: Cho tam thức \(f\left(x\right)=ax^2+bx+c\) (\(a\ne0\)), \(\Delta=b^2-4ac\)
Nếu \(\Delta< 0\) thì \(f\left(x\right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x\in R\)
Nếu \(\Delta=0\) thì \(f\left(x\right)\) luôn cùng dấu với hệ số \(a\), trừ khi \(x=-\dfrac{b}{2a}\)
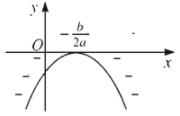
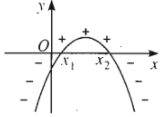
Nếu \(\Delta>0\) thì \(f\left(x\right)\) cùng dấu với hệ số \(a\) khi \(x< x_1\) hoặc \(x>x_2\), trái dấu với hệ số \(a\) khi \(x_1< x< x_2\), trong đó \(x_1,x_2\left(x_1< x_2\right)\) là hai nghiệm của \(f\left(x\right)\).
- Minh hoạ hình học:
Với \(a>0\):
| \(\Delta< 0\) | \(\Delta=0\) | \(\Delta>0\) |
|
|
|
Với \(a< 0\):
| \(\Delta< 0\) | \(\Delta=0\) | \(\Delta>0\) |
|
|
|
@1895638@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Đỗ Thanh Hải đã đóng góp một phiên bản khác cho bài học này (12 tháng 4 2021 lúc 12:49) | 0 lượt thích |