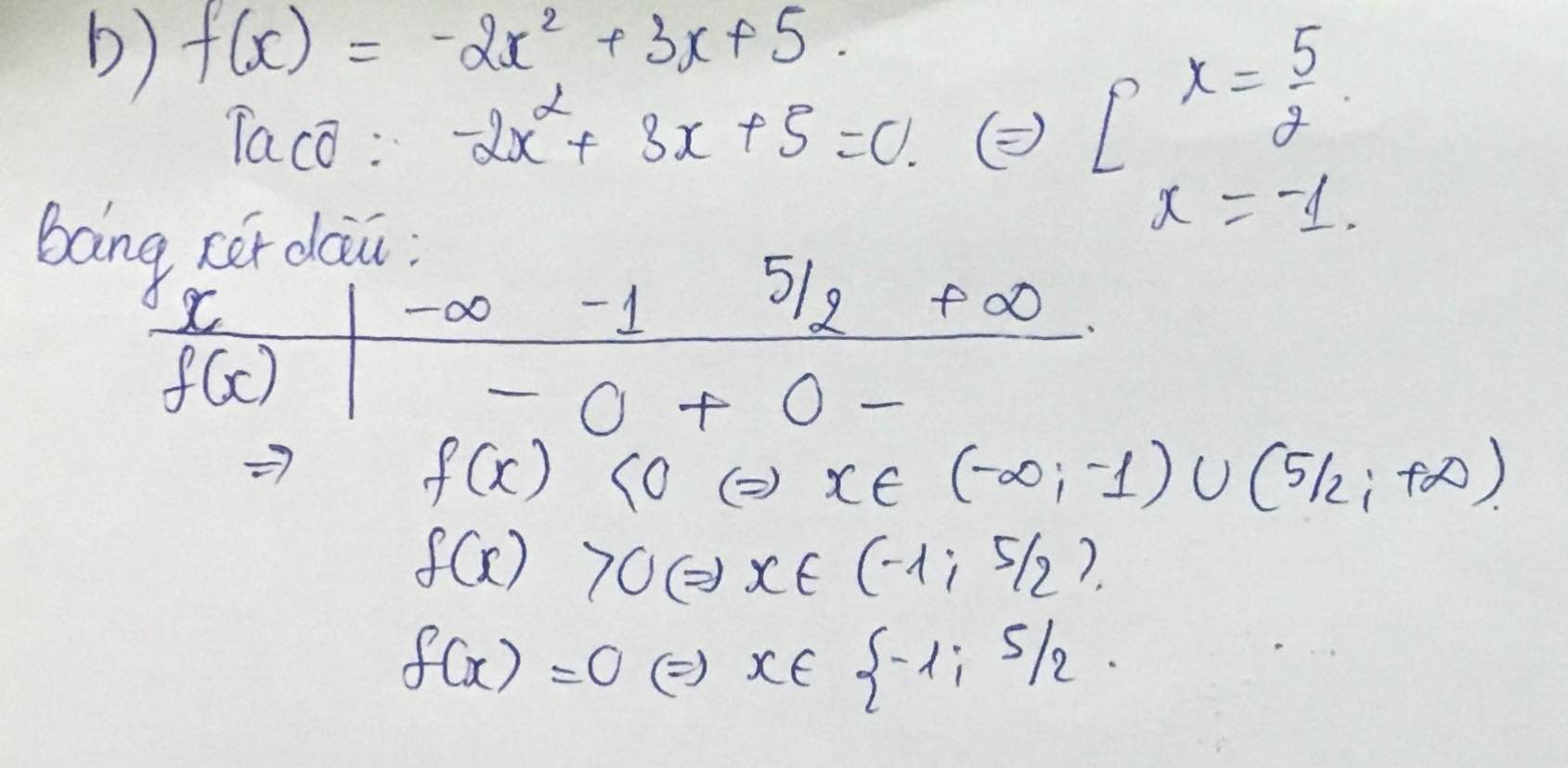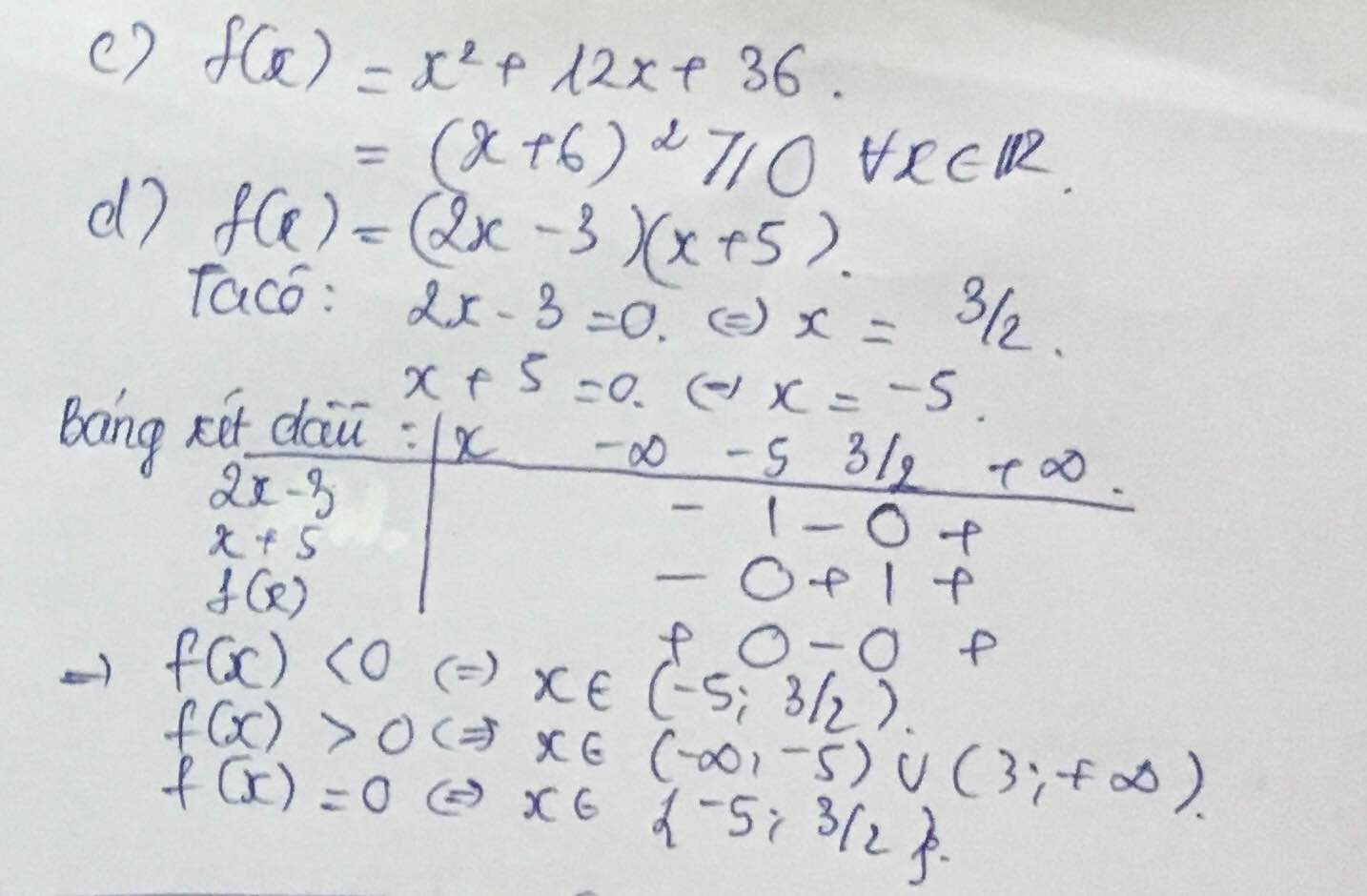§5. Dấu của tam thức bậc hai

a: \(\Delta=\left(m+1\right)^2-4\left(2m+7\right)\)

=m^2+2m+1-8m-28

=m^2-6m-27

=m^2-6m+9-36

=(m-3)^2-36

=(m-9)(m+3)

Để f(x)>0 với mọi x thì (m-9)(m+3)<0 và 1>0

=>-3<m<9

b: x^2+4x+m-5

\(\Delta=4^2-4\left(m-5\right)=16-4m+20=36-4m\)

Để f(x)>0 với mọi x thì 36-4m<0 và 1>0

=>m>9

c: (3m+1)x^2-(3m+1)x+m+4

TH1: m=-1/3

=>11/3>0(luôn đúng)

TH2: m<>-1/3

\(\Delta=\left(3m+1\right)^2-4\cdot\left(m+4\right)\left(3m+1\right)\)

\(=9m^2+6m+1-4\left(3m^2+m+12m+4\right)\)

\(=9m^2+6m+1-12m^2-52m-16\)

\(=-3m^2-46m-15\)

=-(3m^2+46m+15)

=-(3m^2+45m+m+15)

=-(m+15)(3m+1)

Để f(x)>0 với mọi x thì -(m+15)(3m+1)<0 và 3m+1>0

=>(m+15)(3m+1)>0 và 3m+1>0

=>m>-1/3

d: mx^2-12x-5

TH1: m=0

=>-12x-5>0

=>Loại

TH2: m<>0

\(\Delta=\left(-12\right)^2-4\cdot m\cdot\left(-5\right)=20m+144\)

Để f(x)>0 với mọi x thì 20m+144<0 và m>0

=>\(m\in\varnothing\)

a: =>2x^2-x-4x+2<0

=>(2x-1)(x-2)<0

=>1/2<x<2

b: =>5x^2-4x-12>0

=>5x^2-10x+6x-12>0

=>(x-2)(5x+6)>0

=>x>2 hoặc x<-6/5

c: =>(2x+5)^2>0

=>2x+5<>0

=>x<>-5/2

d: =>2x^2-3x+7<=0

Δ=(-3)^2-4*2*7=9-56=-47<0

mà 2>0

nên BPT vô nghiệm

h: =>4x^2+3x-1>0

=>4x^2+4x-x-1>0

=>(x+1)(4x-1)>0

=>x>1/4 hoặc x<-1

g: =>-3x^2-x+4>0

=>3x^2+x-4<0

=>3x^2+4x-3x-4<0

=>(3x+4)(x-1)<0

=>-4/3<x<1

e: Δ=(-4)^2-4*3*4=16-16*3=-32<0

mà 3>0

nên BPT có vô số nghiệm

a: =>3x^2-2x-1>0

=>3x^2-3x+x-1>0

=>(x-1)(3x+1)>0

=>x>1 hoặc x<-1/3

b:=>36x^2-12x+1<=0

=>(6x-1)^2<=0

=>6x-1=0

=>x=1/6

c: =>x^2-6x+9>0

=>(x-3)^2>0

=>x<>3

d: =>(x-3)(x+3)<0

=>-3<x<3

e: =>(x-2căn 2)^2<0(loại)

f: =>x^2-6x-7<=0

=>(x-7)(x+1)<=0

=>-1<=x<=7

g: =>2x^2+8x+4-2x-7/2>=0

=>2x^2+6x+1/2>=0

=>4x^2+12x+1>=0

=>\(\left[{}\begin{matrix}x< =\dfrac{-3-2\sqrt{2}}{2}\\x>=\dfrac{-3+2\sqrt{2}}{2}\end{matrix}\right.\)

\(\dfrac{x^2-3}{x^2-2x}>=2\)

=>\(\dfrac{x^2-3-2x^2+4x}{x^2-2x}>=0\)

=>\(\dfrac{-x^2+4x-3}{x^2-2x}>=0\)

=>\(\dfrac{x^2-4x+3}{x^2-2x}< =0\)

Theo BXD, ta có: 0<x<=1 hoặc 2<x<=3

Pt đã cho có 2 nghiệm pb trái dấu khi:

\(ac< 0\Leftrightarrow2\left(2m^2-3m-5\right)< 0\)

\(\Leftrightarrow-1< m< \dfrac{5}{2}\)