§1. Phương trình đường thẳng

Lời giải;
Vì $AB$ thuộc đường thẳng $3x-y=0$ nên gọi tọa độ của $B$ là $(b, 3b)$

$M$ thuộc đường thẳng $5x+y-8=0$ nên gọi tọa độ $M$ là $(m, 8-5m)$

$M$ là trung điểm $BC$ nên:

$m=x_M=\frac{x_B+x_C}{2}=\frac{b+5}{2}$

$\Rightarrow 2m-b=5(1)$

$8-5m=y_M=\frac{y_B+y_C}{2}=\frac{3b-1}{2}$

$\Rightarrow 16-10m=3b-1$

$\Leftrightarrow 3b+10m=17(2)$

Từ $(1); (2)\Rightarrow m=2; b=-1$

Vậy $B(-1,-3)$ và $M(2, -2)$

$\overrightarrow{BC}=(6, 2)$

$\Rightarrow$ VTPT $BC$ là: $(-2,6)$

PTĐT $BC$: $-2(x+1)+6(y+3)=0$

$\Leftrightarrow -(x+1)+3(y+3)=0$

$\Leftrightarrow -x+3y+8=0$

$A$ là giao điểm của $3x-y=0$ và $5x+y-8=0$ nên $A$ có tọa độ $(1,3)$

$\Rightarrow \overrightarrow{AC}=(4, -4)$

$\Rightarrow$ VTPT $AC$ là $(4,4)$

PTĐT $AC$: $4(x-1)+4(y-3)=0$

$\Leftrightarrow x-1+y-3=0$

$\Leftrightarrow x+y-4=0$

Lời giải;
Vì $AB$ thuộc đường thẳng $3x-y=0$ nên gọi tọa độ của $B$ là $(b, 3b)$

$M$ thuộc đường thẳng $5x+y-8=0$ nên gọi tọa độ $M$ là $(m, 8-5m)$

$M$ là trung điểm $BC$ nên:

$m=x_M=\frac{x_B+x_C}{2}=\frac{b+5}{2}$

$\Rightarrow 2m-b=5(1)$

$8-5m=y_M=\frac{y_B+y_C}{2}=\frac{3b-1}{2}$

$\Rightarrow 16-10m=3b-1$

$\Leftrightarrow 3b+10m=17(2)$

Từ $(1); (2)\Rightarrow m=2; b=-1$

Vậy $B(-1,-3)$ và $M(2, -2)$

$\overrightarrow{BC}=(6, 2)$

$\Rightarrow$ VTPT $BC$ là: $(-2,6)$

PTĐT $BC$: $-2(x+1)+6(y+3)=0$

$\Leftrightarrow -(x+1)+3(y+3)=0$

$\Leftrightarrow -x+3y+8=0$

$A$ là giao điểm của $3x-y=0$ và $5x+y-8=0$ nên $A$ có tọa độ $(1,3)$

$\Rightarrow \overrightarrow{AC}=(4, -4)$

$\Rightarrow$ VTPT $AC$ là $(4,4)$

PTĐT $AC$: $4(x-1)+4(y-3)=0$

$\Leftrightarrow x-1+y-3=0$

$\Leftrightarrow x+y-4=0$

Câu 2: 

sin a=2/7

0<a<pi/2

=>cos a>0

cos^2a=1-(2/7)^2=1-4/49=45/49

=>cosa=3*căn 5/7

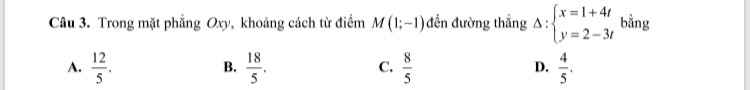
Đường thẳng \(\Delta:\left\{{}\begin{matrix}x=1+4t\\y=2-3t\end{matrix}\right.\) đi qua điểm \(A\left(1;2\right)\) và có VTCP \(\overrightarrow{u}=\left(4;-3\right)\)

\(\Rightarrow\overrightarrow{n}=\left(3;4\right)\) là VTPT của đường thẳng

\(\Rightarrow\) PT tổng quát: \(3\left(x-1\right)+4\left(y-2\right)=0\Leftrightarrow3x+4y-11=0\)

\(\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|3.1+4.\left(-1\right)-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)

a: (d1): 3x+2y-1=0

(d2): 2x-y+1=0

(d1) có vtpt là \(\overrightarrow{a}=\left(3;2\right)\)

(d2) có vtpt là \(\overrightarrow{b}=\left(2;1\right)\)

\(cos\left(d1;d2\right)=\dfrac{\left|3\cdot2+2\cdot1\right|}{\sqrt{3^2+2^2}\cdot\sqrt{2^2+1^2}}=\dfrac{8}{\sqrt{65}}\)

=>(d1;d2)=7 độ

b: (d1); vtpt là vecto a=(5;1)

(d2): x=3+t và y=5-2t

=>VTCP là (1;-2)

=>VTPT là vecto b=(2;1)

\(cos\left(d1;d2\right)=\dfrac{\left|5\cdot2+1\cdot1\right|}{\sqrt{5^2+1^2}\cdot\sqrt{2^2+1^2}}=\dfrac{11}{\sqrt{130}}\)

=>(d1;d2)=15 độ

c: (d1) có vtpt là vecto a=(5;-4)

(d2) có vtpt là vecto b=(4;5)

Vì vecto a*vecto b=0

nên (d1;d2)=90 độ

Con số diện tích lớn quá

\(\overrightarrow{CB}=\left(3;-4\right)\Rightarrow BC=\sqrt{3^2+\left(-4\right)^2}=5\)

\(S=\dfrac{1}{2}d\left(A;BC\right).BC=45\Rightarrow d\left(A;BC\right)=18\)

Theo tính chất trọng tâm, \(d\left(G;BC\right)=\dfrac{2}{3}d\left(A;BC\right)=12\)

Phương trình BC: \(4\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow4x+3y-11=0\)

Do G thuộc \(x-3y+1=0\Rightarrow\) tọa độ G có dạng: \(G\left(3g-1;g\right)\)

\(d\left(G;BC\right)=12\Rightarrow\dfrac{\left|4\left(3g-1\right)+3g-11\right|}{\sqrt{4^2+3^2}}=12\)

\(\Rightarrow\left|g-1\right|=4\Rightarrow\left[{}\begin{matrix}g=5\\g=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}G\left(14;5\right)\\G\left(-10;-3\right)\end{matrix}\right.\)

Áp dụng công thức trọng tâm \(\Rightarrow\left[{}\begin{matrix}A\left(41;9\right)\\A\left(-31;-15\right)\end{matrix}\right.\)

\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;3\right)\) là 1 vtpt

\(d_2\) nhận \(\overrightarrow{n_2}=\left(1;\sqrt{3}\right)\) là 1 vtpt

Gọi \(\alpha\) là góc giữa d1 và d2

\(\Rightarrow cos\alpha=\left|cos\left(\overrightarrow{n_1};\overrightarrow{n_2}\right)\right|=\dfrac{\left|1.1+3.\sqrt{3}\right|}{\sqrt{1^2+3^2}.\sqrt{1^2+3}}=\dfrac{3\sqrt{3}+1}{2\sqrt{10}}\)

\(\Rightarrow\alpha\approx11^034'\)

Gọi \(I\left(5y+5;y\right)\) \(\Rightarrow\overrightarrow{MI}=\left(5y+4;y-2\right)\)

Ta có \(\Delta_1:x-2y+3=0\) có VTPT là \(\vec{n}=\left(1;-2\right)\) nên nó có VTCP là \(\vec{u}=\left(2;1\right)\).

Do đường tròn tâm \(I\) tiếp xúc với \(\Delta_1\) nên \(\overrightarrow{MI}\perp\overrightarrow{u}\)

\(\Rightarrow\overrightarrow{MI}.\overrightarrow{u}=0\Rightarrow2\left(5y+4\right)+1\left(y-2\right)=0\) \(\Rightarrow y=-\dfrac{6}{11}\)

\(\Rightarrow I\left(\dfrac{25}{11};-\dfrac{6}{11}\right)\Rightarrow IM=\dfrac{14\sqrt{5}}{11}\)

Ta có PT đường tròn: \(\left(x-\dfrac{2}{11}\right)^2+\left(y+\dfrac{6}{11}\right)^2=\dfrac{980}{121}\)

Gọi d là đường thẳng qua M và vuông góc \(\Delta_1\)

\(\Rightarrow d\) nhận (2;1) là 1 vtpt

Phương trình d:

\(2\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow2x+y-4=0\)

(C) tiếp xúc \(\Delta_1\) tại M \(\Rightarrow\) tâm I của (C) nằm trên d

\(\Rightarrow I\) là giao điểm d và \(\Delta_2\Rightarrow\) tọa độ I là nghiệm:

\(\left\{{}\begin{matrix}2x+y-4=0\\x-5y-5=0\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{25}{11};-\dfrac{6}{11}\right)\)

\(\Rightarrow\overrightarrow{IM}=\left(-\dfrac{14}{11};\dfrac{28}{11}\right)\Rightarrow R^2=IM^2=\left(-\dfrac{14}{11}\right)^2+\left(\dfrac{28}{11}\right)^2=\dfrac{980}{121}\)

Phương trình (C):
\(\left(x-\dfrac{25}{11}\right)^2+\left(y+\dfrac{6}{11}\right)^2=\dfrac{980}{121}\)

Gọi phương trình đường tròn cần tìm là \(x^2+y^2-2ax-2by+c=0\)

Theo đề, ta có hệ phương trình:

\(\left\{{}\begin{matrix}1+4-2a-4b+c=0\\9+0-6a-2b\cdot0+c=0\\1+16-2a-8b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a-4b+c=-5\\-6a+c=-9\\-2a-8b+c=-17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=3\\c=15\end{matrix}\right.\)

Ta có : \(\overrightarrow{BC}=\left(4;1\right)\) 

Phương trình đường cao của \(\Delta ABC\) kẻ từ A : \(4\left(x-1\right)+1\left(y-4\right)=0\Leftrightarrow4x+y-8=0\)