Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau :
a) \(A\left(3;5\right)\) \(\Delta:4x+3y+1=0\)
b) \(B\left(1;-2\right)\) \(d:3x-4y-26=0\)
c) \(C\left(1;2\right)\) \(m:3x+4y-11=0\)
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau :
a) \(A\left(3;5\right)\) \(\Delta:4x+3y+1=0\)
b) \(B\left(1;-2\right)\) \(d:3x-4y-26=0\)
c) \(C\left(1;2\right)\) \(m:3x+4y-11=0\)
Tìm bán kính của đường tròn tâm \(C\left(-2;-2\right)\), tiếp xúc với đường thẳng \(\Delta:5x+12y-10=0\)
Giải :
Bán kính R của đường tròn tâm C(-2; -2) và tiếp xúc với đường thẳng
∆ : 5x + 12y - 10 = 0 thì bằng khoảng cách từ C đến ∆
R = d(C ;∆) =
=> R = =
.
Xét vị trí tương đối của các cặp đường thẳng \(d_1\) và \(d_2\) sau đây :
a) \(d_1:4x-10y+1=0\) và \(d_2:x+y+2=0\)
b) \(d_1:12x-6y+10=0\) và \(d_2:\left\{{}\begin{matrix}x=5+t\\y=3+2t\end{matrix}\right.\)
c) \(d_1:8x+10y-12=0\) và \(d_2:\left\{{}\begin{matrix}x=-6+5t\\y=6-t\end{matrix}\right.\)
a) Xét hệ \(\left\{{}\begin{matrix}4x-10y+1=0\\x+y+2=0\end{matrix}\right.\)
D = 4.1 = 10.1 = -6 ≠ 0
Vậy d1 và d2 cắt nhau
b) Tương tự, ta có: d1 :\(12x-6y+10=0\) ;
d2= \(2x-y-7=0\)
D = 12 . (-1) - (-6).2 = -12 + 12 = 0
Dx = (-6) . (-7) - (-1). 10 = 42 + 10 = 52 ≠ 0
Vậy d1 // d2
c) Tương tự, ta có d1: \(8x+10y-12=0\)
d2:\(4x+5y-6=0\)
D = 8 . 5 - 4 . 10 = 0
Dx = 10. (-6) - (-12) . 5 = 0
Dy = (-12) . 4 - (-6) . 8 = 0
Vậy d1 trùng d2.
Trả lời bởi Đức MinhTìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau :
a) \(A\left(3;5\right)\) \(\Delta:4x+3y+1=0\)
b) \(B\left(1;-2\right)\) \(d:3x-4y-26=0\)
c) \(C\left(1;2\right)\) \(m:3x+4y-11=0\)
Áp dụng công thức:
d(M0 ;∆) = \(\dfrac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}\)
a) d(M0 ;∆) = \(\dfrac{\left|4\cdot3+3\cdot5+1\right|}{\sqrt{4^2+3^2}}=\dfrac{28}{5}\)
b) d(B ;d) = \(\dfrac{\left|3\cdot1-4\cdot\left(-2\right)-26\right|}{\sqrt{3^2+\left(-4\right)^2}}=-\dfrac{15}{5}=\dfrac{15}{5}=3\)
c) Dễ thấy điểm C nằm trên đường thẳng m : C ε m
Trả lời bởi Đức MinhCho đường thẳng d có phương trình tham số \(\left\{{}\begin{matrix}x=2+2t\\y=3+t\end{matrix}\right.\)
Tìm điểm M thuộc d và cách điểm \(A\left(0;1\right)\) một khoảng bằng 5 ?
Ta có : \(MA=5\leftrightarrow x^2+\left(y-1\right)^2=5^2\)
Thay tọa độ điểm x,y vào tham số t vào pt trên ta được :
\(\left(2+2t\right)^2+\left(3+t-1\right)^2=25\)
\(\Leftrightarrow4t^2+8t+4+4+4t+t^2=25\)
\(\Leftrightarrow5t^2+12t-17=0\rightarrow t_1=1;t_2=-\dfrac{17}{5}\)
Với \(t_1=1\), ta được điểm \(x=4;y=4\Rightarrow M_1\left(4;4\right)\)
Với \(t_2=-\dfrac{17}{5}\)ta được điểm \(x=-\dfrac{24}{5};y=-\dfrac{2}{5}\Rightarrow M_2\left(-\dfrac{24}{5};-\dfrac{2}{5}\right)\)
Trả lời bởi Đức MinhViết phương trình tổng quát của đường thẳng đi qua điểm \(M\left(4;0\right)\) và điểm \(N\left(0;-1\right)\) ?
ta có \(\overrightarrow{MN=}\left(-4;-1\right)\) là vecto chỉ phương của đường thẳng cần tìm ( gọi là đường thẳng d )
Khi đó phương trình đường thẳng d có dạng : \(\left\{{}\begin{matrix}x=-4t\\y=-1-t\end{matrix}\right.\)( khi lấy điểm N là điểm đi qua)
hoặc \(\left\{{}\begin{matrix}x=4-4t\\y=-t\end{matrix}\right.\)( khi lấy điểm M là điểm đi qua)
Trả lời bởi Mông Thái Nhất
Lập phương trình tổng quát của đường thẳng \(\Delta\) trong mỗi trường hợp sau :
a) \(\Delta\) đi qua \(M\left(-5;-8\right)\) và có hệ số góc \(k=-3\)
b) \(\Delta\) đi qua hai điểm \(A\left(2;1\right)\) và \(B\left(-4;5\right)\)
Lập phương trình tham số của đường thẳng d trong mỗi trường hợp sau :
a) d đi qua điểm \(M\left(2;1\right)\) và có vectơ chỉ phương \(\overrightarrow{u}=\left(3;4\right)\)
b) d đi qua điểm \(M\left(-2;3\right)\) và có vectơ chỉ phương \(\overrightarrow{n}=\left(5;1\right)\)
a. phương trình tham số d có dạng : \(\left\{{}\begin{matrix}x=2+3t\\y=1+4t\end{matrix}\right.\)
b. phương trình tham số d có dạng: \(\left\{{}\begin{matrix}x=-2+5t\\y=3+t\end{matrix}\right.\)
Trả lời bởi Mông Thái NhấtCho tam giác ABC, biết \(A\left(1;4\right),B\left(3;-1\right),C\left(6;2\right)\)
a) Lập phương trình tổng quát của các đường thẳng AB, BC, CA
b) Lập phương trình tổng quát của đường cao AH và trung tuyến AM
a) Ta có = (2; -5). Gọi M(x; y) là 1 điểm nằm trên đường thẳng AB thì AM = (x - 1; y - 4). Ba điểm A, B, M thẳng hàng nên hai vec tơ
và
cùng phương, cho ta:
=
<=> 5x + 2y -13 = 0
Đó chính là phương trình đường thẳng AB.
Tương tự ta có phương trình đường thẳng BC: x - y -4 = 0
phương trình đường thẳng CA: 2x + 5y -22 = 0
b) Đường cao AH là đường thẳng đi qua A(1; 4) và vuông góc với BC.
= (3; 3) =>
⊥
nên
nhận vectơ
= (3; 3) làm vectơ pháp tuyến và có phương trình tổng quát:
AH : 3(x - 1) + 3(y -4) = 0
3x + 3y - 15 = 0
=> x + y - 5 = 0
Gọi M là trung điểm BC ta có M \(\left(\dfrac{9}{2};\dfrac{1}{2}\right)\)
Trung tuyến AM là đường thẳng đi qua hai điểm A, M. Theo các viết phương trình đường thẳng đi qua hai điểm trong câu a) ta viết được:
AM : x + y - 5 = 0
Trả lời bởi Đức MinhTìm số đo của góc giữa hai đường thẳng \(d_1\) và \(d_2\) lần lượt có phương trình :
\(d_1:4x-2y+6=0\)
\(d_2:x-3y+1=0\)
Áp dụng công thức cos =
ta có cos =
=> cos =
=
=
=>
= 450
Vậy số đo góc giữa hai đường thẳng \(d_1\) và \(d_2\) là 45 độ.
Trả lời bởi Đức Minh
Áp dụng công thức:
d(M0 ;∆) =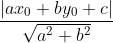
a) d(M0 ;∆) = =
= 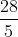
b) d(B ;d) = =
= 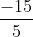 =
= 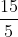 = 3
= 3
c) Dễ thấy điểm C nằm trên đường thẳng m : C ε m.
Trả lời bởi Đức Minh