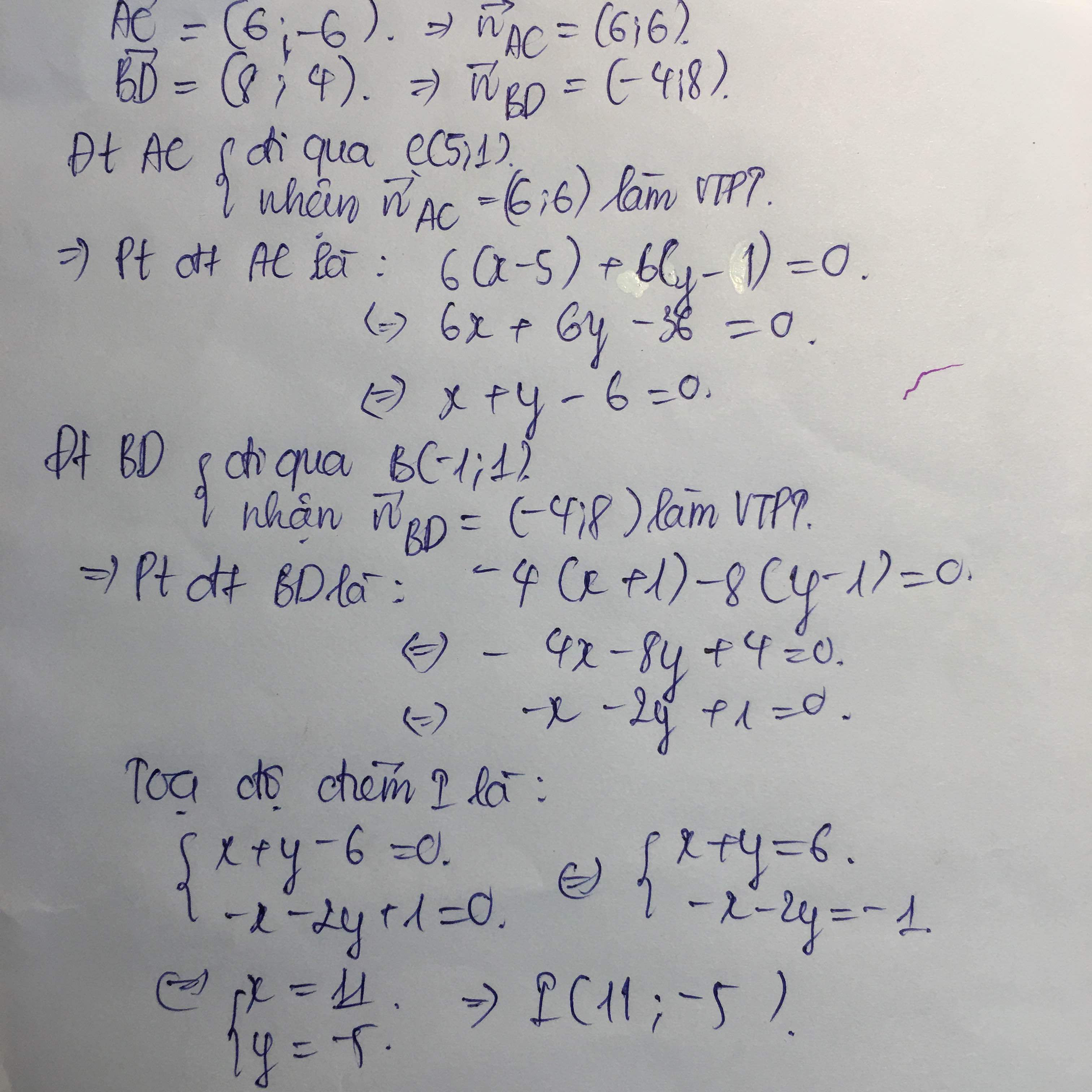trên mặt phẳng tọa độ oxy, cho 3 điểm A(1,1), B(3,2), C(7,10)lập phương trình đường thẳng đenta đi qua A sao cho tổng khoảng cách từ B,C đến đường thẳng đenta là lớn nhất.
§1. Phương trình đường thẳng
Cho ∆ABC, biết A(2;3), B( 3;0). Viết Pt tổng quát của đường thẳng AB.
Ta có:`\vec{AB}=(1;-3) - ` là vtcp của `AB`
`=>` Vtpt của `AB` là: `\vec{n}=(3;1)`
Mà `B(3;0) in AB`
`=>` PTTQ của `AB` là: `3(x-3)+1(y-0)=0`
`<=>3x+y-9=0`
Đúng 5
Bình luận (0)
\(\overrightarrow{AB}=\left(5;-3\right)\)
=>VTPT là (3;5)
Phương trình tổng quát là:
3(x-2)+5(y-3)=0
=>3x-5+5y-15=0
=>3x+5y-20=0
Đúng 3
Bình luận (1)
Làm hộ em câu III ý 1 với ạ 🥺🥺🥺
Lời giải:
Gọi $I(a,b)$ là tâm đường tròn
$(I)$ tiếp xúc với $(d)$ nên: \(R=d(I,(d))=\frac{|a-b+1|}{\sqrt{2}}(*)\)
Mặt khác:
\(\overrightarrow{AB}=(6,-2)\)
\(H(9,4)\) là trung điểm $AB$. \(\overrightarrow{HI}=(a-9,b-4)\)
\(\overrightarrow{HI}\perp \overrightarrow{AB}\Rightarrow 6(a-9)-2(b-4)=0\)
\(\Leftrightarrow 3a-b=23\)
Thay vô $(*)$ thì $R=\frac{|24-2a|}{\sqrt{2}}$
Ta cũng có \(R=IA=\sqrt{(a-6)^2+(b-5)^2}=\sqrt{(a-6)^2+(3a-23-5)^2}\)
\(=\sqrt{10a^2-180a+820}\)
Vậy: \(\frac{|24-2a|}{\sqrt{2}}=\sqrt{10a^2-180a+820}\)
$\Leftrightarrow (24-2a)^2=2(10a^2-180a+820)$
$\Leftrightarrow 16a^2-264a+1064=0$
$\Leftrightarrow 2a^2-33a+133=0$
$\Leftrightarrow a=\frac{19}{2}$ hoặc $a=7$
Đến đây bạn tìm được tâm hình tròn, biết bán kính thì sẽ tìm được pt đường tròn.
Đúng 0
Bình luận (0)
a: vecto KH=(-1;2)
=>BH có vtpt là (2;1) và đi qua K(-1;1)
=>BH: 2(x+1)+1(y-1)=0
=>2x+y+1=0
=>AC: VTPT là (-1;2) và đi qua K(-1;1)
Phương trình AC là:
-1(x+1)+2(y-1)=0
=>-x-1+2y-2=0
=>-x+2y-3=0
=>x-2y+3=0
Đúng 0
Bình luận (0)
giúp em bài này với ạ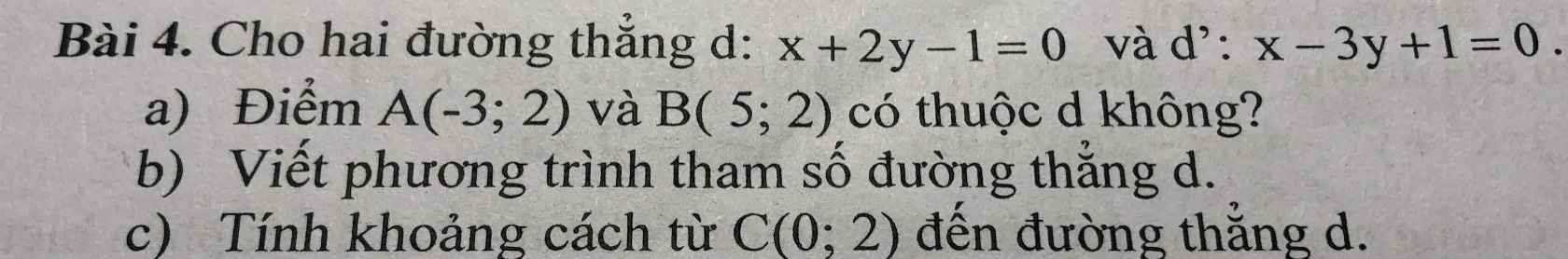
a) Thay \(x=-3;y=2\) vào PT (d) ta được:
\(\left(-3\right)+2.2-1=0\Rightarrow A\in d\)
Thay \(x=5;y=2\) vào PT (d) ta được
\(5+2.2-1=8\ne0\Rightarrow B\notin d\)
b) \(\left(d\right):x+2y-1=0\) có VTPT là \(\overrightarrow{n}=\left(1;2\right)\)
\(\Rightarrow\left(d\right)\) có VTCP là \(\overrightarrow{u}=\left(2;-1\right)\)
PT tham số của (d): \(\left\{{}\begin{matrix}x=-3+2t\\y=2-t\end{matrix}\right.\left(t\in R\right)\)
c) \(d\left(C;\left(d\right)\right)=\dfrac{\left|0+2.2-1\right|}{\sqrt{1^2+2^2}}=\dfrac{3}{\sqrt{5}}=\dfrac{3\sqrt{5}}{5}\)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có A(-1;7) , B(-1;1), C(5;1), D(7;5). Tìm tọa độ giao điểm I của hai đường chéo tứ giác.
rút gọn A= 2cos4xsin3x + cos4x/ -2sin4xsin3x- sin4x
\(=\dfrac{-cos4x\left(2sin3x+1\right)}{sin4x\left(2sin3x+1\right)}=-cot4x\)
Đúng 0
Bình luận (0)
Câu 4: Trong mặt phẳng cho 2 đường thẳng d1: x – y = 0 , d2: x + 2y – 2 = 0 cắt nhau tại điểm A (2;0) và M thuộc d1 và N thuộc d2 Viết phương trình đường thẳng đi qua và cắt d1, d2 tại hai điểm sao cho tam giác có AMN diện tích lớn nhất.
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB AC , widehat{BAC} 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( dfrac{2}{3} ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Đọc tiếp
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB = AC , \(\widehat{BAC}\) = 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( \(\dfrac{2}{3}\) ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb < 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Trong mp tọa độ Oxy cho tam giác ABC. Biết phương trình các đường thẳng chứa đường cao BH, phân giác AD lần lượt làx+4y+5=0; x-y+2=0; điểm M(1; 2) thuộc đường thẳng AB. Tính tọa độ AB