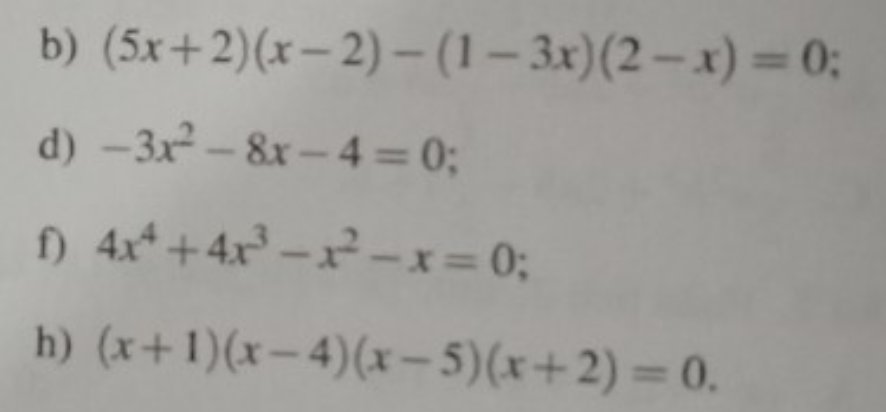b: \(\left(5x+2\right)\left(x-2\right)-\left(1-3x\right)\left(2-x\right)=0\)
=>\(\left(5x+2\right)\left(x-2\right)-\left(3x-1\right)\left(x-2\right)=0\)
=>(x-2)(5x+2-3x+1)=0
=>(x-2)(2x+3)=0
=>\(\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{3}{2}\end{matrix}\right.\)
d: \(-3x^2-8x-4=0\)
=>\(3x^2+8x+4=0\)
=>\(3x^2+6x+2x+4=0\)
=>(x+2)(3x+2)=0
=>\(\left[{}\begin{matrix}x+2=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f: \(4x^4+4x^3-x^2-x=0\)
=>\(4x^3\left(x+1\right)-x\left(x+1\right)=0\)
=>\(x\left(x+1\right)\left(4x^2-1\right)=0\)
=>\(x\left(x+1\right)\left(2x-1\right)\left(2x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+1=0\\2x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
h: (x+1)(x-4)(x-5)(x+2)=0
=>\(\left[{}\begin{matrix}x+1=0\\x-4=0\\x-5=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=4\\x=5\\x=-2\end{matrix}\right.\)
`#3107.101107`
\(\text{b)}\\ \left(5x+2\right)\left(x-2\right)-\left(1-3x\right)\left(2-x\right)=0\\ \Rightarrow\left(5x+2\right)\left(x-2\right)+\left(1-3x\right)\left(x-2\right)=0\\ \Rightarrow\left(x-2\right)\left(5x+2+1-3x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\2x=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy, `x \in {2; -3/2}`
`d)`
`-3x^2 - 8x - 4 = 0`
`\Rightarrow -(3x^2 + 8x + 4) = 0`
`\Rightarrow 3x^2 + 8x + 4 = 0`
`\Rightarrow 3x^2 + 6x + 2x + 4 = 0`
`\Rightarrow 3x(x + 2) + 2(x + 2) = 0`
`\Rightarrow (3x + 2)(x + 2) = 0`
\(\Rightarrow\left[{}\begin{matrix}3x+2=0\\x+2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x=-2\\x=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-2\end{matrix}\right.\)
Vậy, `x \in {-2/3; -2}`
`f)`
\(4x^4+4x^3-x^2-x=0\\ \Rightarrow x\left(4x^3+4x^2-x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\\left(4x^3+4x^2\right)-\left(x+1\right)=0\end{matrix}\right.\\ \Rightarrow4x^2\left(x+1\right)-\left(x+1\right)=0\\ \Rightarrow\left(4x^2-1\right)\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x^2-1=0\\x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}4x^2=1\\x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x^2=\dfrac{1}{4}\\x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
Vậy, `x \in {0; -1; +-1/2}`
`h)`
\(\left(x+1\right)\left(x-4\right)\left(x-5\right)\left(x+2\right)=0\\\Rightarrow \left[{}\begin{matrix}x+1=0\\x-4=0\\x-5=0\\x+2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=4\\x=5\\x=-2\end{matrix}\right.\)
Vậy, `x \in {-1; -2; 4; 5}.`