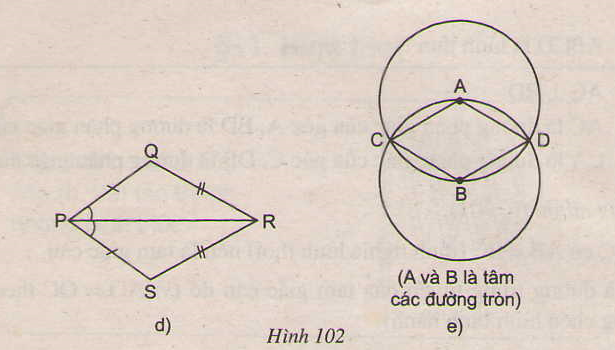
73. Tìm các hình thoi trên hình 102.
Bài giải:
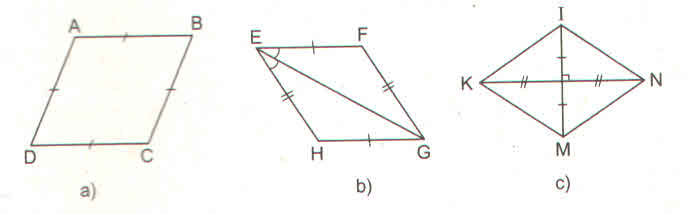
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
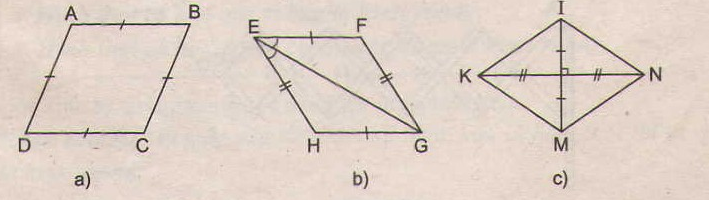
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.


Giải
a) Xét tứ giác ABCD ta có:
AB = BC = CD = DA (gt)
=> Tứ giác ABCD là hình thoi ( tứ giác có bốn cạnh bằng nhau ).
b) Xét tứ giác EFGH ta có:
EF = HG (gt)
EH = FG (gt)
=> Tứ giác EFGH là hình bình hành ( tứ giác có các cạnh đối bằng nhau ).
Xét hình bình hành EFGH ta có:
EG là tia phân giác của góc HEF (gt)
=> Hình bình hành EFGH là hình thoi ( hình bình hành có một đường chéo là đường phân giác của một góc ).
c) Gọi O là giao điểm của IM và KN.
Xét tứ giác KINM ta có:
OI = OM (gt)
OK = ON (gt)
=> Tứ giác KINM là hình bình hành ( tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường ).
Xét hình bình hành KINM ta có:
IM vuông góc với KN.
=> Hình bình hành KINM là hình thoi ( hình bình hành có hai đường chéo vuông góc với nhau ).
d) Tứ giác PQRS không là hình thoi.
e) ADBC là hình thoi ( theo định nghĩa, vì AC = AD = AB = BD = BC ).
Tuy bài này là bài cơ bản chỉ dựa theo dấu hiệu nhận biết của hình bình hành và hình thoi trong sách giáo khoa nhưng lại có một chút nâng cao ở câu e). Mong Sách Giáo Khoa ra thêm nhiều bài hay hơn nữa!