 giải
giải
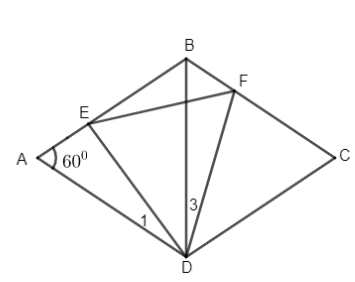
ta có AB=AD(gt)và góc A=60 độ nên tam giác DEF đều=>BD=AD
Tương tự tam giác DEF đều =>góc CBD=60độ
Từ BE+BF=BD=>AE=BF
Xét tam giác AED và tam giác BFD có:
AD=BD(cmt)
góc A=góc CBD=60 độ
AE=BF
Do đó tam giác AED=tam giác BFD(c,g.c)
=>DE=DF
nên tam giác DEF cân (1)
Và góc D1=góc D3 nên góc D1+góc EBD=60độ =>góc D3+góc EBD=60độ (2)
Từ (1) và (2) suy ra tam giác DEF đều.

